1.4.1 Распределение Максвелла

В состоянии теплового равновесия как бы не изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул в газе, при Т=cоnst, остается постоянной и равной .

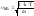Это объясняется тем, что в газе устанавливается некоторое стационарное статистическое распределение молекул по значениям скоростей, называемое распределением Максвелла. Распределение Максвелла описывается некоторой функцией f(), называемой функцией распределения молекул по скоростям.

,где N – общее число молекул, dN() – число молекул, скорости которых принадлежат интервалу скоростей от  до  + d.

Таким образом, функция Максвелла f() равна вероятности того, что величина скорости наугад выбранной молекулы принадлежит единичному интервалу скоростей вблизи значения . Или она равна доле молекул, скорости которых принадлежат единичному интервалу скоростей вблизи значения .

Явный вид функции f() был получен теоретически Максвеллом:

.

График функции распределения приведен на рис. 12. Из графика следует, что функция распределения стремится к нулю при 0 и  и проходит через максимум при некоторой скорости _В, называемой наиболее вероятной скоростью. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно _В. Значение наиболее вероятной скорости можно найти, используя условие для максимума функции f().

.

На рис. 13 показано смещение _В с изменением температуры, при этом площадь под графиком остается постоянной и равной 1, что следует из условия нормировки функции Максвелла

.

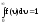Условие нормировки следует из смысла данного интеграла – он определяет вероятность того, что скорость молекулы попадает в интервал скоростей от 0 до . Это достоверное событие, его вероятность, по определению, принимается равной 1.

Знание функции распределения молекул газа по скоростям позволяет вычислять средние значения любых функций скорости, в частности средней арифметической скорости <>.

.

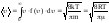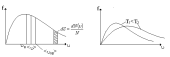
Рис.12 Рис. 13

По функции Максвелла можно определить долю молекул, скорости которых принадлежат заданному интервалу скоростей или превышают некоторое значение скорости, например вторую космическую, что определяет рассеяние атмосферы.

.

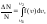
1.4.2 Распределение Больцмана

Тепловое движение частиц тела приводит к тому, что положение их в пространстве изменяется случайным образом. Поэтому можно ввести функцию распределения частиц по координатам, определяющую вероятность обнаружения частицы в том или ином месте пространства.

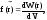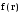
где  плотность вероятности, т.е. вероятность обнаружения частицы в единичном объеме вблизи точки с радиус-вектором .

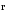При отсутствии внешних силовых полей существует равномерное распределение частиц идеального газа по координатам, при этом можно записать

,

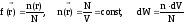где n  концентрация частиц, N  полное число частиц газа.

Внешнее силовое поле изменяет пространственное распределение частиц, при этом концентрация частиц и функция распределения зависят от координат. Если внешнее силовое поле является потенциальным, то концентрация частиц вблизи точки пространства с радиусом-вектором зависит от потенциальной энергии частиц в данном месте:

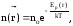где n_o  концентрация частиц в том месте, где E_p=0.

В этом случае вероятность обнаружить частицу в объеме dV вблизи точки с радиусом-вектором определяется выражением

.

Этот закон называется распределением Больцмана.

Для идеального газа давление связано с концентрацией соотношением Р=nkT. В поле земного тяготения концентрация изменяется с высотой над поверхностью Земли, и если газ находится в равновесном состоянии при температуре Т, то изменение давления с высотой происходит по закону

.

Последнее соотношение называется барометрической формулой. В действительности земная атмосфера не находится в равновесном состоянии, ее температура меняется с высотой, и барометрическую формулу следует применять к участкам атмосферы, в пределах которых изменением температуры можно пренебречь. Из барометрической формулы следует, что давление различных газов изменяется с высотой по-разному. На рис. 14 показано изменение давления газа с высотой для различных газов при T = const, а на рис. 15 – изменение давления газа ( = const) при разных температурах.