Методические рекомендации
Данные для выполнения задания взять из таблицы 1.
Пример выполнения задания – рис. 14.
Для выполнения графического задания необходимо изучить способы преобразования комплексного чертежа.
Работу начать с построения по заданным координатам треугольника АВС, основания пирамиды. Определить угол между плоскостями АВС и BCS, используя две замены плоскостей проекций.
Рекомендуется придерживаться расположения изображений согласно образцу.
Однако при определении натуральных величин основания пирамиды АВС и ребра AS необходимо самостоятельно выбрать положение осей вращения так, чтобы в итоге получилось не только правильное, но и наглядное решение задачи.
Оформить графическую работу в соответствии с образцом (рис. 14).
Последовательность выполнения
Определить угол между плоскостями АВС и BCS способом замены плоскостей проекций.
Ввести новую фронтальную плоскость F параллельно стороне ВС. Провести линии связи перпендикулярно оси x и отложить на них высоту, равную расстоянию по оси z. Соединить точки с учетом видимости. Ввести новую горизонтальную плоскость Н перпендикулярно стороне ВС. Провести линии связи перпендикулярно оси х (точки В и С проецируются по одной линии связи) и отложить на них расстояние, равное координате y (отмерять от оси х1). Соединить точки и замерить угол ABC ∧ BCS.
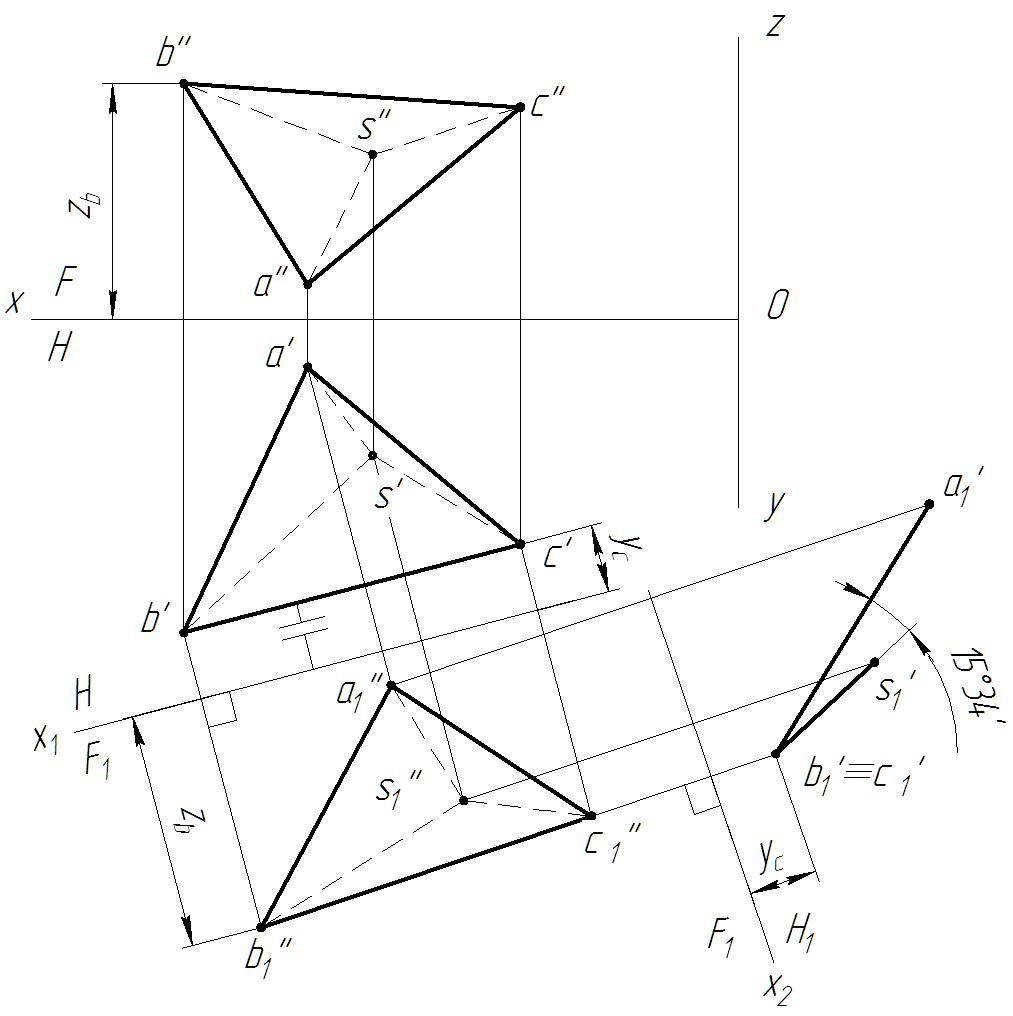
Рисунок 10 – Нахождение двугранного угла способом замены плоскостей проекций
Определить истинную величину основания пирамиды ABC способом плоскопараллельного перемещения и способом вращения вокруг линии уровня.
Плоскопараллельным перемещением переносим основание АВС так, чтобы горизонталь С1 стала перпендикулярна оси х. От вновь построенных точек а, b и с проводим вертикальные линии связи до пересечения с горизонтальными линиями связи на фронтальной проекции. Отмечаем полученные точки (фронтальная проекция основания АВС должна выродиться в линию). Фронтальную проекцию a, b, c поворачиваем относительно оси i до горизонтального положения (параллельно оси х). Опускаем линии связи вертикально вниз до пересечения с горизонтальными линиями связи. Отмечаем точки. a', b', c' – натуральная величина основания АВС.
Рисунок 11 – Нахождение натуральной величины основания АВС способом плоскопараллельного перемещения
Проводим фронталь c'1', c''1''. Опускаем перпендикуляр из точки a'' к фронтали. Отмечаем точку o'' (прямая a''o'' является радиусом вращения точки А вокруг фронтали С1). Определяем натуральную величину радиуса a''o'' методом прямоугольного треугольника. Поворачиваем точку a относительно точки o'' до пересечения с продолжением перпендикуляра a''o''. Отмечаем точку А. Из точки А проводим прямую через точку 1''. Из точки b'' проводим перпендикуляр к фронтали c''1''. В месте пересечения отмечаем точку В. Соединяем точки А, В, С – натуральная величина основания АВС найдена.
Рисунок 12 – Нахождение натуральной величины основания АВС способом вращения вокруг линии уровня
Определить натуральную величину ребра AS вращением вокруг проецирующей оси.
В свободном месте чертежа вычерчиваем отдельно две проекции ребра AS. Через точку А проводим проецирующую линию (ось вращения i перпендикулярна фронтальной плоскости проекции). Фронтальную проекцию ребра a''s'' вращаем до положения, параллельного оси х. Проводим линии связи от проекции a''s0'' на горизонтальную плоскость проекций. От горизонтальной проекции ребра a's' проводим линии направления движения до пересечения с линиями связи. Горизонтальная проекция a's0' – есть натуральная величина ребра AS.
Рисунок 13 – Нахождение натуральной величины ребра способом вращения
Таблица 1 – Исходные данные
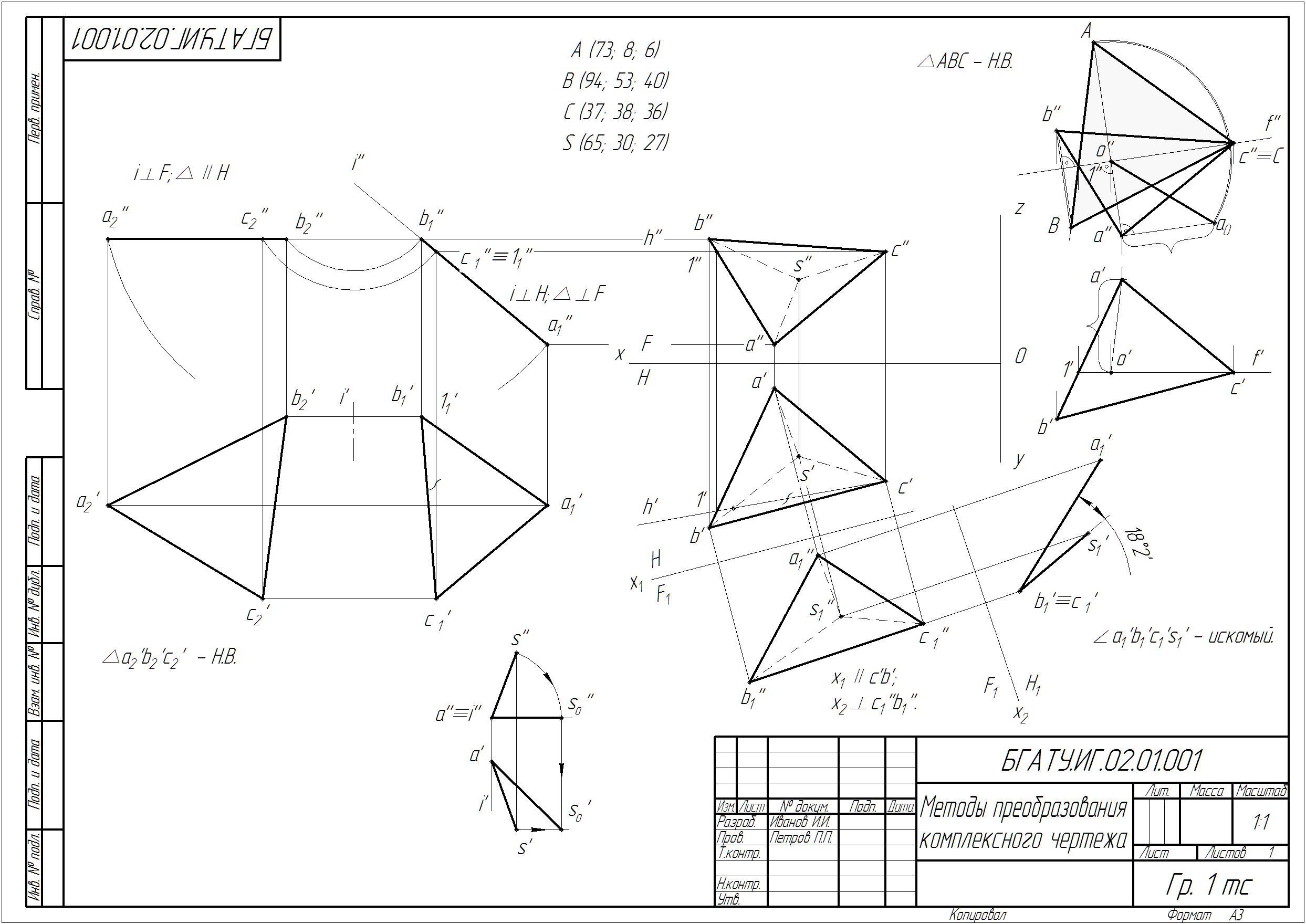
Рисунок 14 – Образец выполнения задания «Способы преобразования чертежа»