
- •Часть II электричество и магнетизм Техника безопасности
- •Основные электроизмерительные приборы
- •Оценка погрешностей электрических измерений
- •Изучение электростатических полей методом электролитического моделирования
- •Теория метода и описание установки
- •Напряженностью электрического поля в данной точке называется физическая величина, численно равная силеF, с которой электрическое поле действует на единичный зарядq, помещенный в данную точку поля:
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Здесь g – баллистический гальванометр;
- •Порядок выполнения работы
- •Контрольные вопросы
- •Измерения и обработка результатов измерений
- •Контрольные вопросы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Порядок выполнения работы
- •Контрольные вопросы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Порядок выполнения работы
- •Контрольные вопросы
- •Порядок выполнения работы
- •Определение коэффициента самоиндукции
- •Определение емкости конденсатора
- •Проверка закона Ома
- •Контрольные вопросы
- •Литература
- •Содержание
Порядок выполнения работы
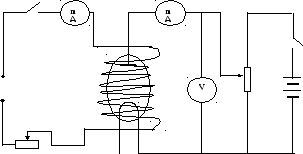
Собрать электрическую цепь по схеме (рис 3).
Цепь соленоида ключом
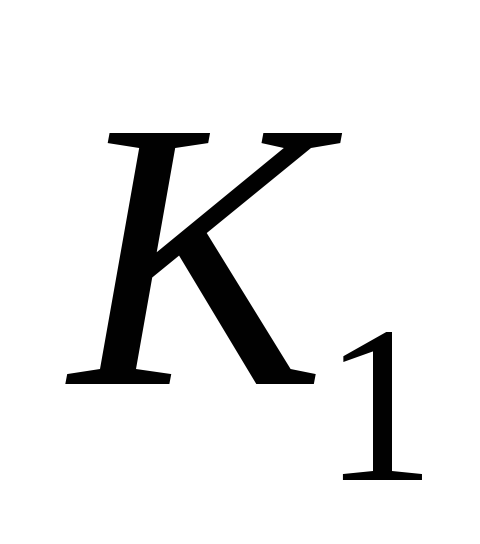 разомкнуть
(
разомкнуть
(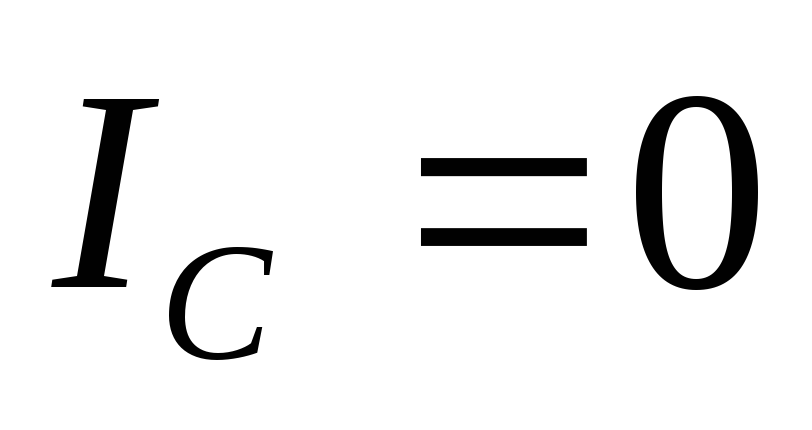 ).
).Замкнуть ключом
 анодную цепь и реостатом
анодную цепь и реостатом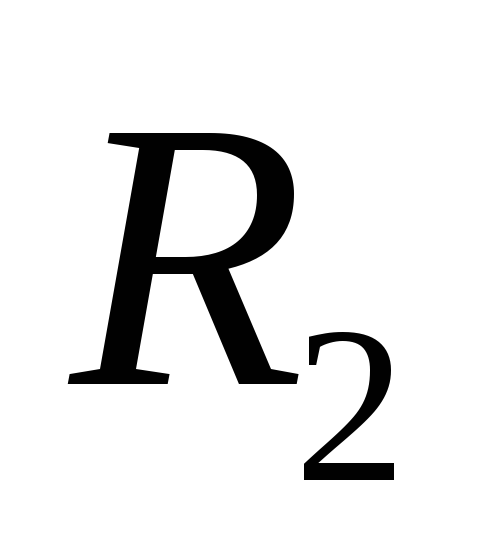 подать на анод лампы напряжение (
подать на анод лампы напряжение (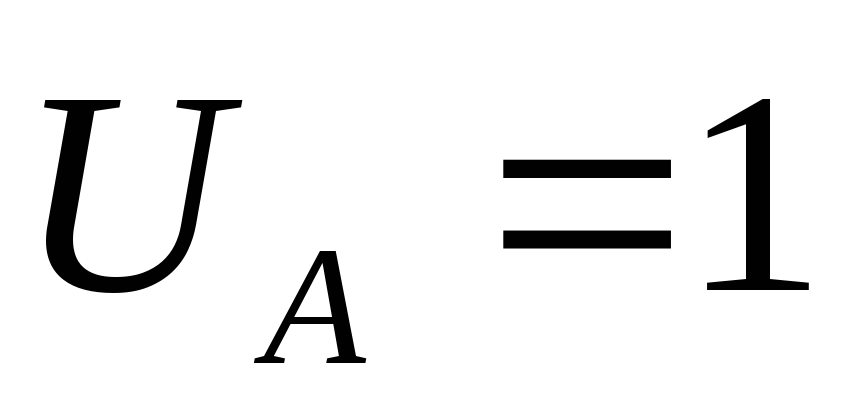 В).
В).Записать величину анодного тока
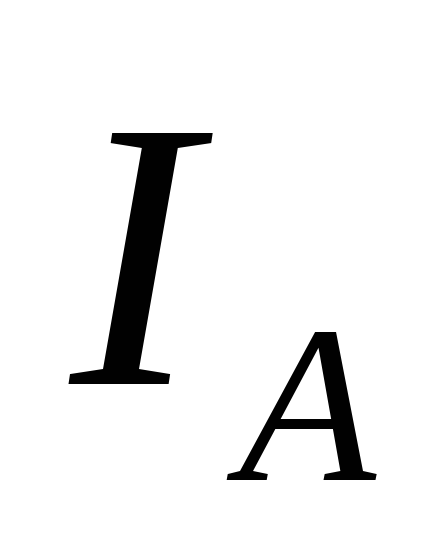 .
.Включить с помощью ключа
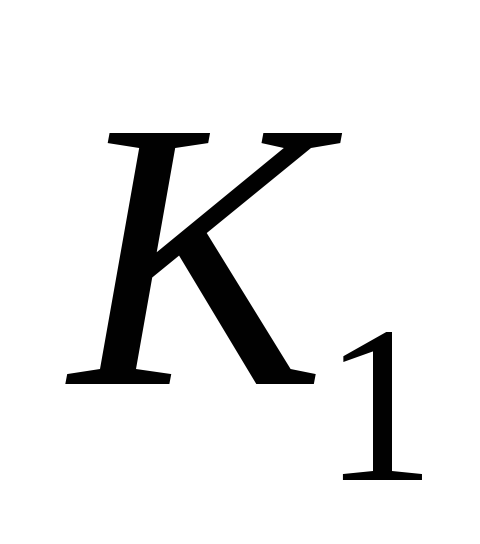 цепь соленоида.
цепь соленоида.С помощью реостата
 увеличивать ток в цепи соленоида от
увеличивать ток в цепи соленоида от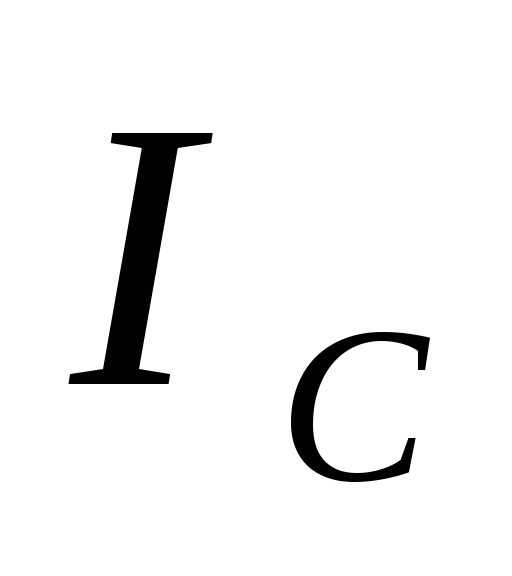 =0
до
=0
до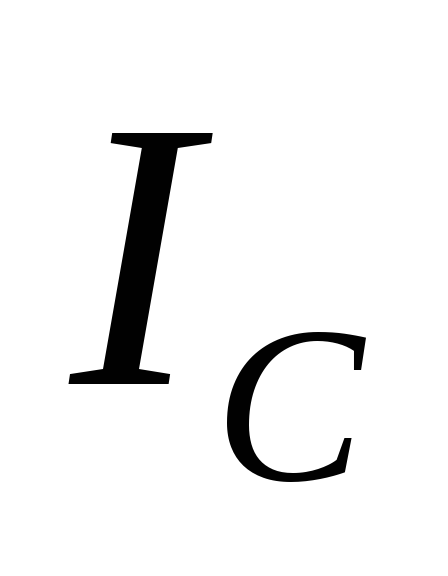 =200
мА через
=200
мА через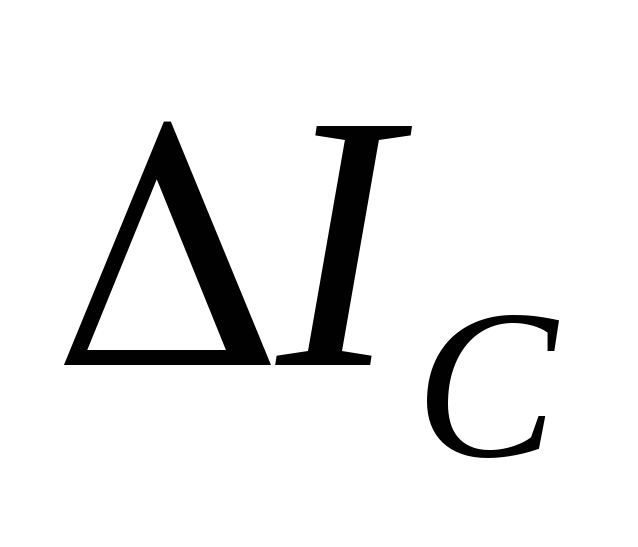 =20
мА и записывать в таблицу соответствующие
им значения тока
=20
мА и записывать в таблицу соответствующие
им значения тока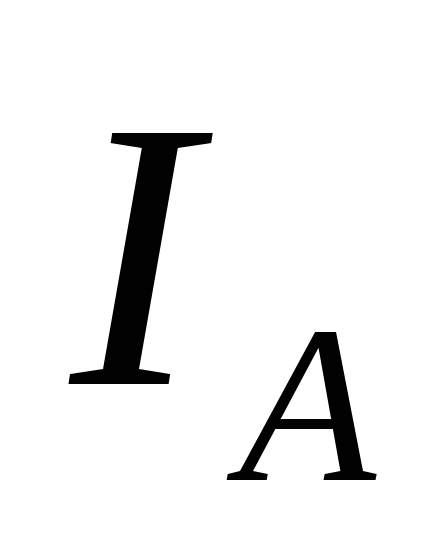 .
.По полученным данным построить график зависимости
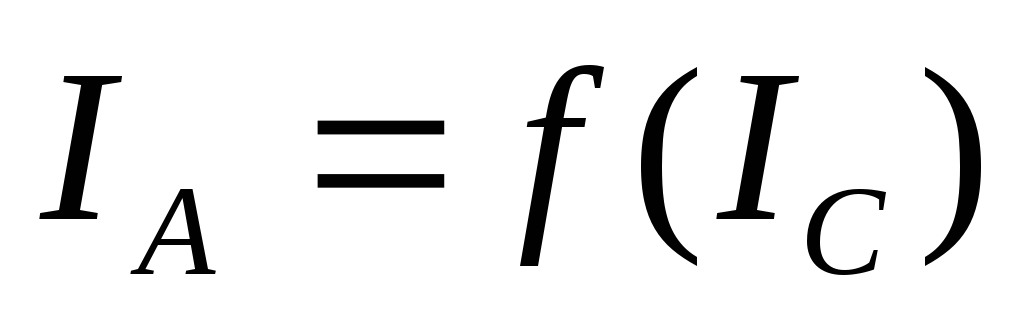 (рис 4), из него найти критическое
значение тока (
(рис 4), из него найти критическое
значение тока (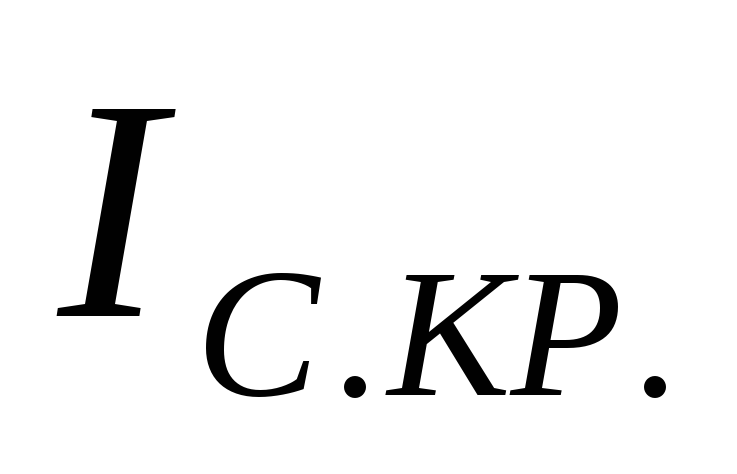 )
соленоида.
)
соленоида.Измерив длину
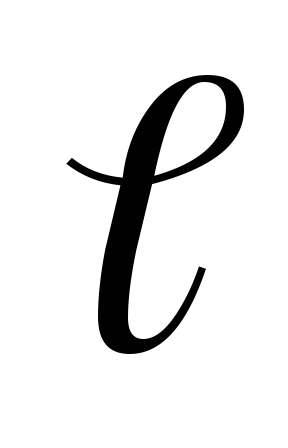 соленоида и диаметр его поперечного
сечения, найти
соленоида и диаметр его поперечного
сечения, найти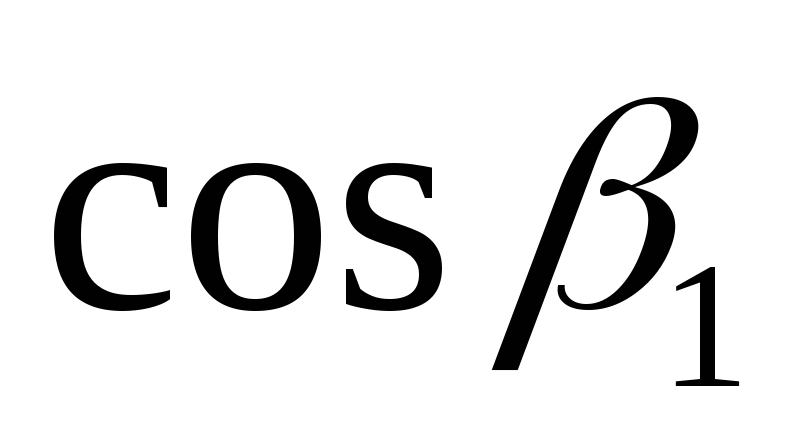 и
и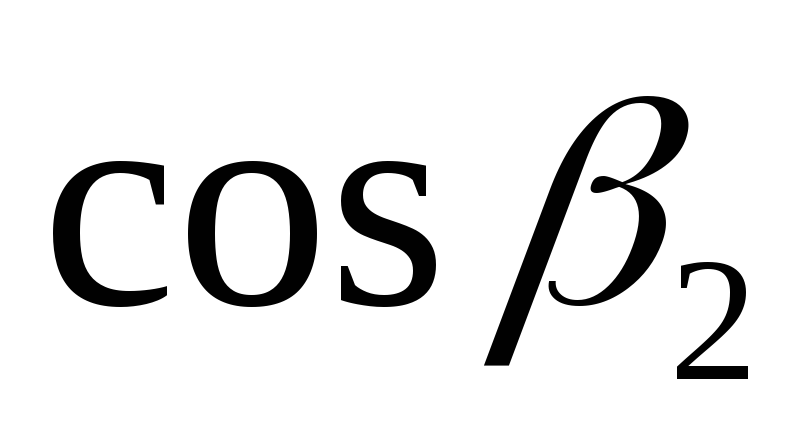 .
.Рассчитать по формуле (10)
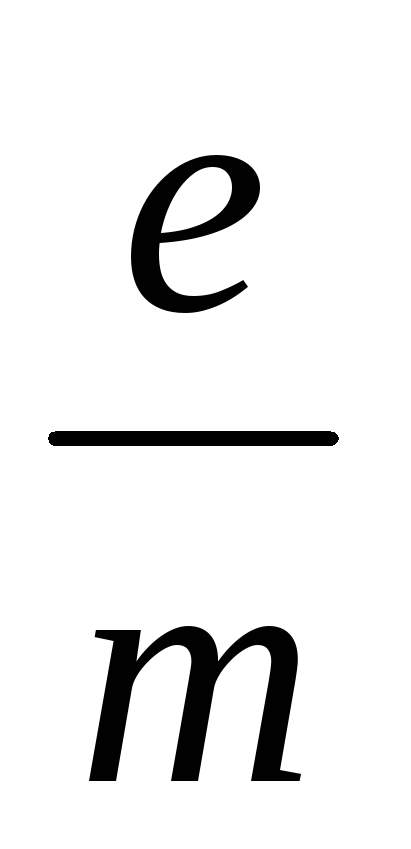 .
Значения N
и b
указаны на панели прибора.
.
Значения N
и b
указаны на панели прибора.Повторить опыты для других значений
 .
.
Контрольные вопросы
В чем заключается метод измерения удельного заряда, примененный в данной работе?
Объясните устройство и принцип действия магнетрона.
Какие силы действуют на заряд в электрическом поле? В магнитном поле?
Запишите формулу для силы Лоренца. Укажите, как определить направление ее действия?
Выведите формулу (10).
Используя табличные данные о заряде и массе электрона, определите значение удельного заряда электрона и, сравнив его с полученным Вами в лабораторной работе, оцените, насколько корректно Вы выполнили лабораторную работу.
Литература
1. Курс общей физики А.С. Шубин
2. Курс физики Р.И. Грабовский
![]()
А
![]()
![]()
0 – 400 В 6 В
К


![]() 2,15 В
2,15 В
Рис 3.

![]()
![]()
![]()
Рис 4
ЛАБОРАТОРНАЯ РАБОТА № 2.8
ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ
НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
Приборы и принадлежности: магнит, компас, секундомер
Теория метода и описание установки
Магнитное поле Земли представляет собою как бы огромный магнит, полюса которого лежат вблизи географических полюсов: вблизи северного географического полюса расположен южный магнитный S, а вблизи южного географического – северный магнитный N (рис. 1)
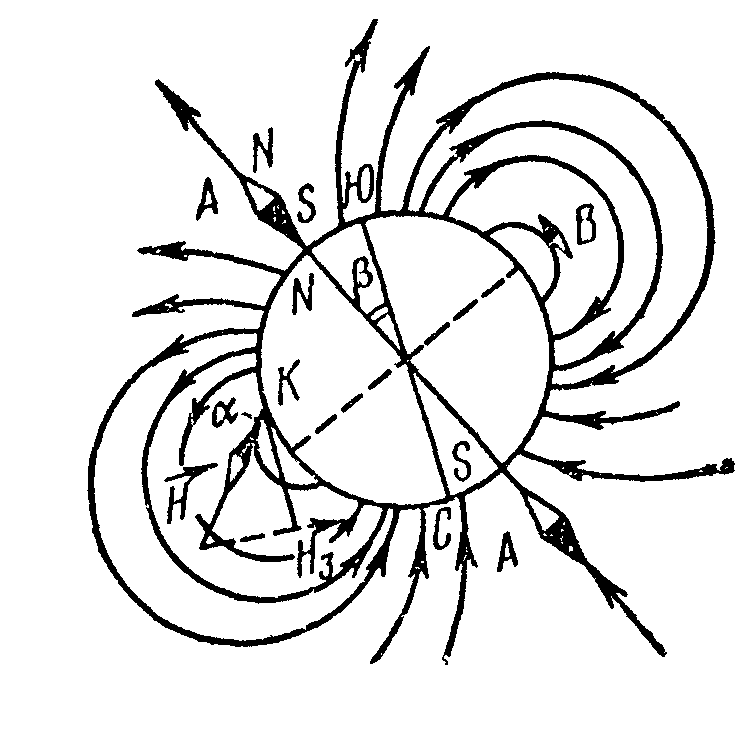
Рис 1.
Магнитное поле Земли на экваторе направлено горизонтально (точка В), а у магнитных полюсов – вертикально (точка А). В остальных точках земной поверхности магнитное поле Земли направлено под некоторым углом (точка К).
Величину проекции
напряженности земного магнитного поля
![]() на горизонтальную плоскость называют
горизонтальной составляющей магнитного
поля Земли
на горизонтальную плоскость называют
горизонтальной составляющей магнитного
поля Земли ![]() .
Направление этой составляющей принимается
за направление магнитного меридиана,
а вертикальная плоскость, проходящая
через него, называется плоскостью
магнитного меридиана.
Угол
.
Направление этой составляющей принимается
за направление магнитного меридиана,
а вертикальная плоскость, проходящая
через него, называется плоскостью
магнитного меридиана.
Угол
![]() между направлением магнитного поля
Земли и горизонтальной плоскостью
называют углом наклонения,
а угол
между направлением магнитного поля
Земли и горизонтальной плоскостью
называют углом наклонения,
а угол
![]() между географическим и магнитным
меридианами - угол склонения.
между географическим и магнитным
меридианами - угол склонения.
Магнитная
стрелка, которая может вращаться лишь
около вертикальной оси, будет отклоняться
в горизонтальной плоскости только под
действием горизонтальной составляющей
напряженности
![]() магнитного поля Земли.
магнитного поля Земли.
Существуют
постоянные магниты, магнитное поле
которых создается молекулярными токами.
Поле прямолинейного магнита подобно
полю соленоида. Как и катушка с током,
полосовой магнит характеризуется
некоторым магнитным моментом
![]() .
Напряженность магнитного поля на
достаточно большом расстоянии от системы
с магнитным моментом
.
Напряженность магнитного поля на
достаточно большом расстоянии от системы
с магнитным моментом![]() (контур
с током, постоянный магнит) определяется
формулой (в системе СИ):
(контур
с током, постоянный магнит) определяется
формулой (в системе СИ):
![]() , (1)
, (1)
ч то
иллюстрируется рисунком 1
то
иллюстрируется рисунком 1![]()
![]()
![]()
![]()
Р ис
1
ис
1
Возьмем магнит в форме призматического стержня и подвесим его на тонкой и длинной нити так, чтобы он занимал горизонтальное положение (рис 2) .
S N Магнит устанавливается в направлении
магнитного меридиана (упругость нити пренебрежимо мала).
Если стержень вывести из положения равновесия (в горизонтальной плоскости), то на него будет действовать вращающий момент М
![]() ,
(2)
,
(2)
Рис
2 где
![]() - горизонтальная составляющая напряженности
магнитного поля Земли, а
- горизонтальная составляющая напряженности
магнитного поля Земли, а![]() - угол отклонения от положения равновесия.
Под воздействием механического момента
возникают крутильные колебания.
Пренебрегая трением и упругостью нити,
можно записать уравнение:
- угол отклонения от положения равновесия.
Под воздействием механического момента
возникают крутильные колебания.
Пренебрегая трением и упругостью нити,
можно записать уравнение:
![]()
или
![]() ,
,
где
I
– момент инерции магнита. При малых
углах
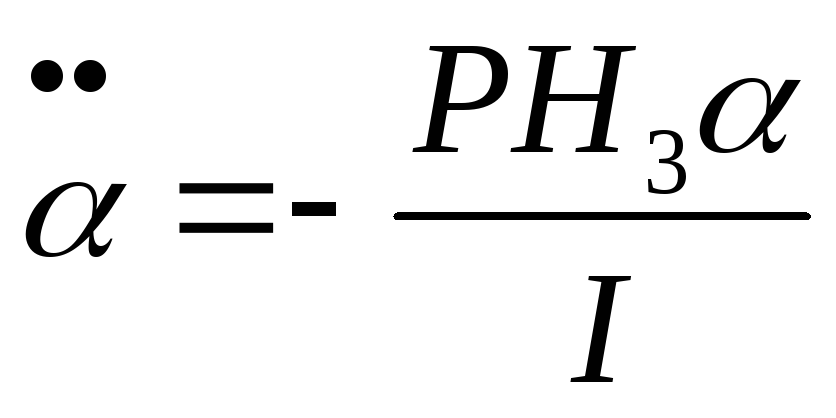 .
.
Введя
подстановку
![]() ,
получим:
,
получим:
![]() (3)
(3)
Уравнение (3) – это дифференциальное уравнение гармонического колебательного движения. Его решение имеет вид:
![]() ,
(4)
,
(4)
где
![]() - амплитуда колебаний;
- амплитуда колебаний;
![]() -
циклическая частота.
-
циклическая частота.
Период колебаний равен:
![]() (5)
(5)
Момент инерции призматического магнита относительно оси , проходящей через центр тяжести перпендикулярно к его длине, вычисляется по формуле:
![]() ,
(6)
,
(6)
где
![]() -
длина магнита;
-
длина магнита;
![]() -
ширина магнита
-
ширина магнита
![]() -
масса магнита.
-
масса магнита.
В
уравнение (5) входит еще неизвестная
величина Р. Рассмотрим второй опыт,
который позволит найти связь между
![]() и Р.
и Р.
Возьмем скамью со шкалой и с помощью буссоли, прикрепленной на ее конце, установим ее перпендикулярно магнитному меридиану. После этого возьмем магнит, который должен подвешиваться на нити, и расположим его на скамье так, как показано на рисунке 3.

![]() Н
Н
![]()
N
![]()
 S N
S N
Рис 3. S
Стрелка
буссоли при этом отклонится на некоторый
угол
![]() ,
отсчитываемый по
,
отсчитываемый по
шкале буссоли. Из рисунка видно, что
![]() ,
(7)
,
(7)
где
![]() - напряженность магнитного поля,
создаваемого постоянным магнитом в
месте расположения буссоли. Из уравнения
(1) найдем
- напряженность магнитного поля,
создаваемого постоянным магнитом в
месте расположения буссоли. Из уравнения
(1) найдем![]() ,
принимая
,
принимая![]() и
и![]() :
:
![]()
Отсюда
![]() (8)
(8)
Решая
совместно уравнения (5), (6), (7) и (8),
найдем
![]() :
:
![]() (9)
(9)
Чтобы
исключить ошибку, зависящую от несовпадения
магнитной оси буссоли с ее геометрической
осью, угол
![]() отсчитывают от обеих концов стрелки.
Для исключения ошибки на неточность
установления буссоли магнит поворачивают
около вертикальной оси на
отсчитывают от обеих концов стрелки.
Для исключения ошибки на неточность
установления буссоли магнит поворачивают
около вертикальной оси на![]() и повторяют измерения угла
и повторяют измерения угла![]() .
Из четырех полученных значений находят
среднее, которым пользуются в дальнейших
вычислениях.
.
Из четырех полученных значений находят
среднее, которым пользуются в дальнейших
вычислениях.
Следует помнить, что формула (9) справедлива в системе СИ.
