
Danilyuk_20TV_20i_20MS
.pdf
41
Зокрема, якщо Y C const, то D(X C) D(X), тобто дисперсія випадкової величини Х не зміниться від додавання до неї сталої величини. Дійсно
D X C M X C M X C 2 M X C M X M C 2
M X C M X C 2 M X M X 2 D X .
Властивість 4. Дисперсія приймає тільки невід’ємні значення, тобто
D(X) 0.
Ця властивість випливає із означення дисперсії.
Середнім квадратичним відхиленням випадкової величини Х називають корінь квадратний із дисперсії:
(Х) 
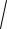 D(x).
D(x).
Задача 3.3.1. Дискретна випадкова величина Х задається рядом розподілу
|
X |
|
-1 |
|
0 |
1 |
2 |
|
3 |
|
|
P |
|
0,2 |
|
0,1 |
0,3 |
0,3 |
|
0,1 |
|
Знайти: а) М(Х); |
|
б) М(Х2+1); |
в) D(X); |
г) D(3Х); |
д) D(2Х-1); |
|||||
е) Р(-1<X 2); є) (Х).
Розв’язання. а) По формулі (3.3.1) маємо
M(X) xi pi 10,2 0 0,1 10.,3 30,1 1;
б)M (X 2 1) M (X 2 ) 1 ( 1)2 0,2 02 0,1 12 0,3 22 0,3 32 0.1 1 3,6;
в) D(X) M(X2) (M(X))2 2,6 1 1,6; г) D(3X) 9D(X) 91,6 14,4;
д) D(2X 1) D(2X) 4D(X) 41,6 6,4;
е)P( 1 X 2) P(X 0) P(X 1) P(X 2) 0,1 0,3 0,3 0,7;
є) (X) 
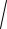 D(X)
D(X) 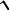
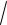 16 1,265.
16 1,265.
Відповідь: а) 1; б)3,6; в) 1,6; г) 14,4; д) 6,4; е) 0,7; є) 1,265
Задача 3.3.2. Випадкова величина Х задається функцією розподілу
|
|
|
|
|
0, |
|
x 1, |
|
|
|
||
|
|
|
|
|
(x 1)2 |
|
|
|
|
|||
|
|
|
|
F(x) |
, |
1 x 0, |
|
|
|
|||
|
|
|
|
|
|
|
x 0. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1, |
|
|
1 |
|
|
1 |
|
Знайти: а) М(Х); б) М( |
|
Х |
|
) в) D(Х); г) D(2Х+1); д) Р( |
|
Х |
) |
|||||
|
|
|||||||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
3 |
|
||
|
|
|
|
|
|
|
||||||
Розв’язання. а) Знайдемо щільність розподілу випадкової величини

42
|
0, |
x 1, |
|
|
|
||
1 x 0, |
|||
f (x)F (x) 2(x 1) , |
|||
|
|
x 0. |
|
|
0, |
|
|
Користуючись формулою (3.3.3), знайдемо
0 |
0 |
2 |
|
1 |
|
|
3 |
|
1 |
|
2 |
|
0 |
|
1 |
|
1 |
|
|
1 |
|
M(X) x 2(x 1)dx 2 (x |
|
x)dx 2( |
|
|
x |
|
|
|
x |
|
) |
1 |
2 |
|
|
|
|
|
|
; |
|
|
3 |
|
2 |
|
|
|
3 |
||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
3 2 |
|
|
|
||||||
б) Користуючись формулою (3.3.4), знаходимо
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
|
M( |
X |
) |
|
x |
|
2(x 1)dx 2 ( x)(x 1)dx 2 (x2 1)dx |
; |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
в) Користуючись формулою (3.3.7), знаходимо |
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
x3 |
|
0 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
D(X) x22(x 1)dx ( |
|
|
)2 |
|
2 |
(x3 x2)dx |
|
|
|
|
2( |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
3 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 3 |
1 9 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2( |
1 |
|
1 |
) |
1 |
|
1 |
|
1 |
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
3 |
9 |
|
|
|
6 |
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
г) D(2X 1) D(2X) 4D(X) 4 |
1 |
|
|
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
д)P( |
1 |
X |
1 |
|
) F( |
1 |
) F( |
1 |
) ( |
1 |
1) |
2 |
( |
|
1 |
|
1) |
2 |
|
4 |
|
|
1 |
|
|
7 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
2 |
3 |
3 |
2 |
3 |
|
|
2 |
|
9 |
|
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|||||||||||||||||||||||
Відповідь. а) |
|
|
|
1 |
; б) |
1 |
; в) |
|
1 |
; г) |
|
2 |
; д) |
|
7 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
18 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задачі для самостійного розв’язання.
Задача 3.3.3. |
Дискретна випадкова величина задається рядом розподілу |
|||||||
|
|
|
|
|
|
|
|
|
X |
-3 |
|
-2 |
-1 |
0 |
1 |
2 |
3 |
P |
0,1 |
|
0,15 |
0,1 |
0,3 |
0,1 |
0,15 |
0,1 |
Знайти: а) М(Х); б) М( Х ); в) D(X); г) D(3X-4); д) (Х).
Відповідь: а) 0; б) 1,4; в) 3,2; г) 28,8; д) 1,79.
Задача 3.3.4. Дискретна випадкова величина Х може приймати тільки два значення: х1 і х2, причому х1 < х2. Ймовірність Р(Х=х1)=р1=0,3; М(Х)=3,7; D(X)=0,21. Знайти закон розподілу випадкової величини Х.
Відповідь:
X |
3 |
4 |
P |
0,3 |
0,7 |

43
Задача 3.3.5. Випадкова величина Х задається функцією розподілу
0, x 0, F(x) x2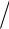 4, 0 x 3,
4, 0 x 3,
1, x 3.
Знайти: а) М(Х); б) D(X); в) (X).
Відповідь: а) 2; б) 1 ; в) 0,71.
2
Задача 3.3.6. Випадкова величина Х задається функцією розподілу
|
|
3 |
3 |
x x 0 |
|
|
|
x , |
|
1 x |
|
0 |
||
F(x) |
0 |
|
x x0 |
|
0, |
|
|
|
|
|
|
|
|
|
Знайти: а) М(Х); б) D(X); в) (X).
Відповідь: а) 3х0 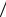 2; б)3х02
2; б)3х02 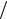 4;в)
4;в) 
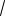 3х0
3х0 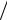 2.
2.
3.4.ДЕЯКІ РОЗПОДІЛИ ЙМОВІРНОСТЕЙ
1.Дискретні розподіли:
а) Біноміальний розподіл. Біноміальним називають закон розподілу дискретної випадкової величини Х – числа появи в n незалежних випробувань, в кожному з яких ймовірність появи події дорівнює р; ймовірність можливого значення Х=к (числа к появи події) обчислюють з допомогою формули Бернулі:
P (k) Ck pkqn k, q 1 p, |
k 0,n. |
|
n |
n |
|
Для того, щоб розподіл |
був ймовірносним розподілом, необхідно, щоб |
|
pk 1. |
|
|
Дійсно, по формулі біному Ньютона |
|
|
n |
n |
|
pk cnk pkqn k p q 1. |
|
|
k 0 |
k 0 |
|
Легко підрахувати, що для випадкової величини М(Х)=np, D(X)=npq.
б) Пуассоновський розподіл. Пуассоновським називають закон розподілу дискретної випадкової величини Х, в тому випадку, коли число n випробувань велике, а ймовірність появи події р в кожному випробуванні мала, і ймовірність можливого значення Х=к обчислюється по формулі Пуассона
P (k) |
(np)ke np |
|
|
|
|
||
|
, |
k=0,1, … |
|
|
|
||
|
|
|
|
||||
n |
k! |
|
|
|
|
||
|
|
x |
k |
||||
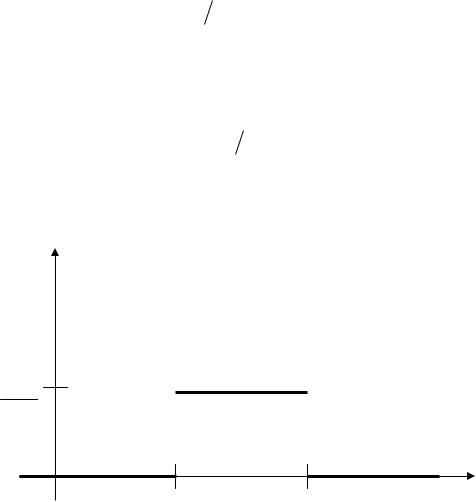
Перевіримо, що pk |
|||||||
1. Враховуючи, що ex |
|
, отримаємо |
|||||
|
|
||||||
|
|
|
k 0 |
k! |
|||
44
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
e |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
pk |
|
|
|
e |
|
|
|
e e |
1. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
k 0 |
|
k! |
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Знайдемо числові характеристики пуассонівського розподілу: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k |
e |
|
|
|
|
|
k |
e |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
m |
e |
|
|
|
|
|
|
|
|
||||||||||||
M X |
k |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||||||||||||||||||||||
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 1 ! |
|
|
|
|
|
k 1 ! |
|
0 |
|
m! |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M |
|
X2 |
|
|
k2 ke |
|
e |
|
|
|
|
k k 1 |
e |
|
|
k 1 1 |
k 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
k! |
|
|
|
|
|
|
|
k 1 ! |
|
|
|
|
|
|
|
|
|
|
|
|
k 1 ! |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
k |
1 |
k 1 |
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
|
|
k 1 |
|
||||||||||||||||
|
e |
|
|
e |
|
|
|
|
|
|
2e |
|
|
|
|
|
e |
|
|
. |
|||||||||||||||||||||||||||||||
|
|
k 1 ! |
k 1 ! |
|
|
|
|
|
|
k 1 ! |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
k 2 |
k 2 ! |
|
k 1 |
|
||||||||||||||||||||||||||||
Оскільки кожна з цих сум дорівнює e , то
M X2 2e e e e 2 .
Отже, дисперсія величини X дорівнює
D X 2 2 .
2. Неперервні розподіли а) Рівномірний розподіл. Рівномірним називають розподіл ймовірностей
неперервної випадкової величини Х, можливі значення якої належать інтервалу (а,в ) і її щільність розподілу задається формулою
0, |
x a, |
|
a x в, |
f (x) 1 (в a), |
|
|
х в. |
0, |
Функція розподілу для рівномірного розподілу має вигляд
0, |
x a, |
|
a x в, |
F(x) (x a) (в а)б, |
|
|
х в, |
1, |
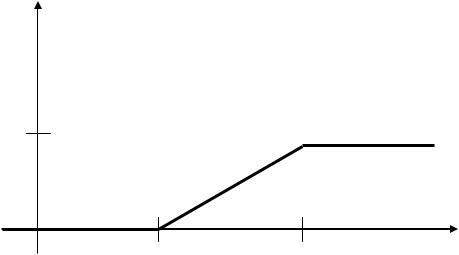
Графіки для щільності розподілу і функції розподілу мають вигляд
f x
1
в а
45
0 |
а |
в |
х |
F x
1
0 а в х
а числові характеристики М(X) |
в а |
|
|
|
D(X) |
|
(в а)2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
|
b |
2 |
a |
2 |
|
|
a b |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
M X xf x dx x |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 b a |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
b a |
|
|
|
|
|
b a 2 |
|
a |
|
|
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
D X x2 |
f x dx M |
X |
|
2 b |
|
x2 |
dx a b 2 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b a |
|
|
|
|
4 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||||||||||
|
1 x3 |
|
b |
a b 2 |
b3 a3 |
|
|
a b |
2 |
|
|
b a b2 ab a2 |
|
a b 2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3b a |
3 b a |
|
|
|
|
|
|
|
|
|
|
|
|
3 b a |
|
|
|
|
|||||||||||||||||||||||||||
|
|
a |
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
b2 |
ab a2 |
a2 |
2ab b2 |
|
|
|
b2 2ab a2 |
|
b a 2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
12 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
б) Показниковий (ексионенціальний) розподіл. Показниковим називають розподіл ймовірностей неперервної випадкової величини Х, який описується щільністю розподілу

46
0, |
x 0, |
f (x) |
x 0, |
e x, |
|
|
|
де - стала додатня величина. |
|
Функція розподілу такої величини має вигляд
0, |
x 0, |
|
F(x) |
||
x 0. |
||
1 e x, |
||
|
|
Математичне сподівання, дисперсія і середнє квадратичне віджилення показничого розподілу відповідно дорівнюють:
M(X) |
1 |
, |
D(X) |
1 |
, (X) |
1 |
: |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x u, |
|
|
|
|
|
du dx |
|
|
|
|
|
||||||||||||||||
M X x e xdx |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
e |
|
|
dv, |
|
|
v |
|
|
e |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
e x |
|
|
|
|
e xdx. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
По правилу Лопіталя |
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
xe x |
|
lim |
|
lim |
|
|
0. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
0 |
|
|
|
x e x |
|
x e x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
e x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
M X e xdx |
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогічно, з допомогою двократного інтегрування по частинах і використовуючи правило Лопіталя, отримаємо
D X |
1 |
|
X |
|
|
1 |
. |
|
, |
D X |
|||||||
2 |
|
|||||||
|
|
|
|
|
|
|||
Нехай T - кількість годин, які попрацював прилад до першої поломки. Експериментально доведено, що T має експоненціальний розподіл, а функція розподілу випадкової величини T
F x P T x 1 e x
називається функцією надійності.
Ймовірність попадання в інтервал ( , ) неперервної випадкової величини Х, розподіленої по показниковому законі обчислюється з допомогою формули
P( X ) e e .
Задачі для самостійного розв’язання.
47
Задача 3.4.1. Середня величина годин праці приладу до першої поломки 100. T - години праці приладу – має показників розподіл. Знайти ймовірності
а) прилад пропрацював від 80 до 110 годин; б) прилад пропрацював менше 50 годин.
Розв’язання. З умови задачі маємо M T |
1 |
100, |
0,01, |
|
|
||||
|
x 0 |
|
||
0, |
|
|||
f x |
. |
|
||
0,01e 0,01x, |
x 0 |
|
||
а) Ймовірність, що прилад пропрацює від 80 до 100 годин:
P 80 T 100 e 80 0,01 e 100 0,01 e 0,8 e 1,1 0,449 0,333 0,116
б) Ймовірність, що прилад пропрацює менше 50 годин:
P T 50 P 0 T 50 e0 e 50 0,01 1 e0,5 1 0,607 0,393.
Задача 3.4.2. Проводиться 6 дослідів, в кожному з яких подія може відбутися з ймовірністю 0,4. Нехай Х – випадкова величина, що дорівнює числу успіхів в дослідах. Знайти: а) М(Х); б) D(X); в) (Х); г) ймовірність того, що успіхів у досдах буде менше 2.
Відповідь. а) 2,4; б) 1,44; в) 1,2; г) 0,065.
Задача 3.4.3. Випадкова величина Х розподілена по пуассоновському законі з параметром np 2. Знайти ймовірності; а) Р(X<2); б) P(X=3)
Відповідь. в) 0,406; б) 0,180.
Задача 3.4.4. Відомо, що число визовів, які поступають на АТС, є пуассоновська випадкова величина з параметром np 0t де 0 - середнє число визовів за 1 хвилину, t - час. Нехай 0 =2. Знайти ймовірність того, що за 4 хвилини поступить: а) три визови; б) менше трьох визовів; в) не менше трьох визовів.
Відповідь. а) 0,256; б) 0,0123; в) 0,9877.
Задача 3.4.5. Ціна поділки шкали вимірювального прибору 0,2. Показання прибору заокруглюють до найближчої цілої поділки. Знайти ймовірність того, що при відліку буде зроблена помилка:
а) менша 0,04; б) більша 0,05.
Відповідь. а) 0,4; б) 0,5.
Задача 3.4.6. Тривалість часу безвідмовної роботи елементу має показниковий розподіл F(t)=1-e-0,01t. Знайти: а) середній час безвідмовної роботи елементу; б) ймовірність того, що за час тривалістю 50 годин елемент відмовить.
Відповідь. а) 100 год; б) 0,394.

48
3.5. НОРМАЛЬНИЙ РОЗПОДІЛ.
Серед розподілів неперервних випадкових величин Х центральне місце займає нормальний закон (закон Гауса), щільність розподілу ймовірностей якого має вигляд
|
1 |
|
е |
(х а) |
2 |
|
|
f (x) |
|
2 2 |
, |
||||
|
|
|
|||||
|
|
||||||
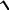 2
2
де а= М(Х) – математичне сподівання, 
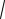 D(x) - середнє квадратичне
D(x) - середнє квадратичне
відхилення величин Х.
Нормальний закон проявляється в усіх тих випадках, коли випадкова
величина Х є результатом дії великого числа різних факторів. Прикладами
випадкових величин, що мають нормальний розподіл, можуть служити:
відхилення дійсних розмірів деталей, оброблених на станку, від номінальних
розмірів, помилки при вимірюваннях, відхилення від цілі при стрильбі і т.д.
Функція розподілу для нормального закону має вигляд
|
|
1 x |
(z a)2 |
|
||||
|
|
|
2 |
|
||||
F(x) |
|
|
|
|
e |
2 |
|
dz. |
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
2 |
|
|
|
|||
Припустимо, що випадкова величина Х має нормальний закон розподілу. Тоді ймовірність того, що Х прийме значення, яке належить інтервалу ( , ) знаходиться з допомогою формули
|
|
|
|
|
|
|
|
a |
|
a |
|
||
P( X ) |
|
|
|
, |
(3.5.1) |
||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
x |
|
z2 |
|
|
|
|
|
|
|
де Ф(х)= |
|
|
e |
|
dz - |
функція |
Лапласа, яка була |
розглянута вище. |
|||||
|
|
2 |
|||||||||||
|
|
|
|
||||||||||
|
|
||||||||||||
|
|
2 0 |
|
|
|
|
|
|
|
|
|
||
Ймовірність того, що абсолютна величина відхилення менша додатнього числа
P( |
|
X a |
|
|
|
|
|
|
|
|
|||||
|
|
) 2 |
|
. |
(3.5.2) |
||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 3.5.1 . Вага виробу має нормальний закон з а=3000 г і 10г. знайти ймовірності: а) вага виробу не менша 2990 г і не більша 3005 г; б) вага виробу відхиляєть від середнього значення а не більше ніж на 15г.
49
Розв’язання. Оскільки випадкова величина Х – вага виробу підкоряється нормальному закону розподілу ймовірностей, то справеливі формули (3.5.1) і (3.5.2).
а) P(2990 X 3005 ) (3005 3000 ) (2990 3000 ) (0,5) (1) 10 10
По таблиці (Додаток 1) знаходимо Ф(0,5)=0,1915, Ф(1)=0,3413 і тоді
P(2990 X 3005) 0,1915 0,3413 0,5328 .
б) при 15 г по формулі (3.5.2) знаходимо
P( X 3000 |
15) 2 (15 ) 2 (1,5) 2 0,4332 |
0,8664 . |
10
Відповідь. а) 0,5328; б) 0,8664.
Візьмемо в якості 3 , тоді
P X a 3 2Ф 3 2Ф 3 0,9973.
На основі останньої рівності застосовується правило "3 x ігм": якщо випадкова величина розподілена нормально, то абсолютна величина її відхилення від математичного сподівання не перевищує потрійного середнього квадратичного відхилення.
Якщо a 0, 1, то розподіл називається стандартним.
Задачі для самостійного розв’язання.
Задача 3.5.2. Випадкова величина Х задається щільністю розподілу ймовірностей
1 |
|
|
(x 3)2 |
||||||||
|
|
|
|||||||||
f (x) |
|
|
|
|
|
e 8 . |
|||||
|
|
|
|
|
|||||||
2 2 |
|||||||||||
|
|
|
|
|
|
|
|||||
Знайти: а) P(1 X 4,5);б) P( |
|
X 3 |
|
1). |
|
|
|
|
|||
|
|
|
|
|
|
||||||
Відповідь: а) 0,6147; б) 0,383.
Задача 3.5.3. Довжина виробу є випадкова величина, яка має нормальний закон розподілу з середнім значенням (проектною довжиною) а=10000 мм і середнім квадратичним відхиленням 25 мм. Знайти ймовірності: а) довжина виробу знаходиться в межах 9990 мм до 10050 мм; б) довжина виробу відхиляється від середнього не більше ніже на 50 мм.
Відповідь. а) 0,6326; б) 0,9544.
3.6. СИСТЕМИ ВИПАДКОВИХ ВЕЛИЧИН

50
Нехай X іY - дві випадкові величини. Випадкові величини X іY називаються незалежними, якщо закон розподілу кожної з них не залежить від того, яке значення прийняла друга. Відмітимо, що сталу величину можна розглядати як випадкову величину, незалежну від любих інших випадкових величин.
Як уже відмічалось, тільки для незалежних випадкових величин
справедливі рівності |
|
|
M XY M X M Y , |
D X Y D X D Y . |
(3.6.1) |
Для описання системи двох випадкових величин крім математичного сподівання і дисперсії складових користуються і іншими характеристиками.
Кореляційним моментом xy випадкових величин X іY називають математичне сподівання добутку відхилень цих величин
xy M X M X Y M Y
з (3.6.1) випливає, що якщо X іY незалежні, то xy 0.
З означення кореляційного моменту випливає, що він має розмірність, яка дорівнює добутку розмірностей величин X іY , тобто величина кореляційного моменту залежить від одиниць виміру випадкових величин.
Коефіцієнтом кореляції rxy випадкових величин X іY називають
відношення кореляційного моменту до добутку середніх квадратичних відхилень цих величин:
r |
|
|
|
|
xy |
|
; |
|
|
|
|
|
|||
xy |
|
|
y |
||||
|
|
|
|
|
x |
||
rxy - безрозмірна величина, для якої |
|
rxy |
|
1. |
|
|
|
|
|
|
|
||||
Якщо X іY незалежні, то rxy 0; якщо між X іY є лінійний зв’язок, тобто
якщо Y aX b, то rxy 1, причому rxy 1, якщо a 0, rxy 1, якщо a 0. Розглянемо, як обчислюються xy і rxy у випадку, коли X іY дискретні
випадкові величини. |
|
|
x1,x2, ,xn |
|
|
|
|||
Нехай |
X |
може |
приймати |
значення |
|
з |
ймовірностями |
||
px, px, , px ; Y |
може |
приймати |
значення |
y ,y |
, ,y |
m |
з |
ймовірностями |
|
1 2 |
n |
|
|
|
1 2 |
|
|
|
|
p1y, p2y, , pmy .
Позначимо через xi,yj - ймовірність того, що X прийме значення xi і
одночасно Y прийме значення yj , тобто xi,yj P X xi Y yj . Тоді
