Файловый архив студентов. Файловый архив студентов.
1306 вузов, 5172 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Донбасская национальная академия строительства и архитектуры
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Коваль ЕЛЕМЕНТИ МАТ. ПЕРЕТВОРЕНЬ

.pdf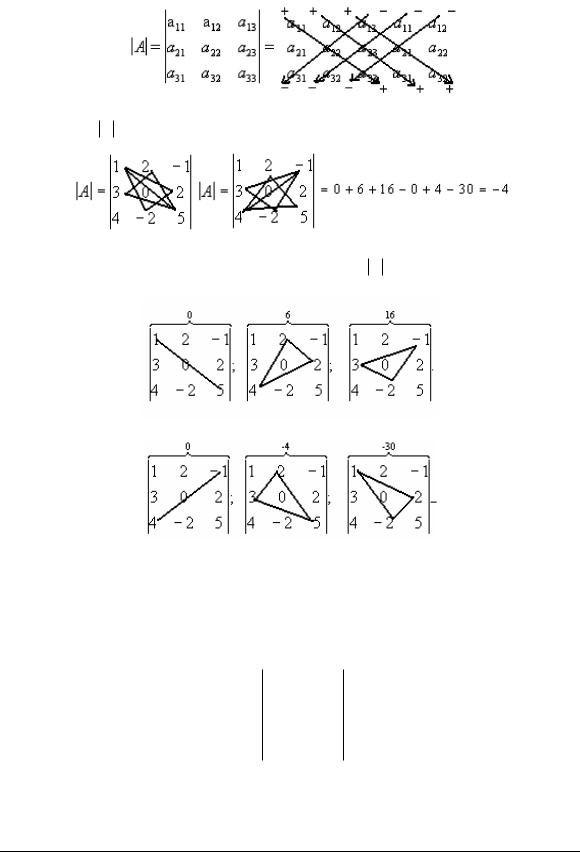
Скачиваний:
19
Добавлен:
21.02.2016
Размер:
4.64 Mб
Скачать
☆

Обчислити детермінант матриці А розміром 3 3 можна згідно з властивістю

(18)або правилом Сарруса (Sarrus):

=a11a22a33 a21a32a13 a12a23a31 a31a22a13 a11a23a32 a21a12a33.

Визначимо A за правилом Сарруса:

Правило Сарруса часто називають правилом трикутника. Далі поступово проілюстріруємо обчислення всіх членів визначника A .

Члени зі знаком “плюс”:

Члени зі знаком “мінус”:

Користуючись поняттям детермінанта, дамо інше означення рангу матриці.

Означення 1.21. Рангом матриці А називається найвищий порядок відмінного від нуля мінора цієї матриці.

Якщо rg A=r, то це означає, що серед мінорів матриці є, зрештою, хоча б один мінор r-го порядку, відмінний від нуля, тоді коли всі мінори вищого порядку: r+1, r+2 і т.д. дорівнюють нулю.

Нехай потрібно знайти ранг матриці А:

1 2

1

A

3

0

2

 

4

2

5

.

 

 

4

2

 

 

2

 

Згідно з означенням рангу матриці його значення не може перевищувати 3. Обчислемо один з визначників третього по порядку матриці А;

11

 

1

2

1

 

A

 

 

3

0

2

4 0.

 

 

4

2

5

 

Отже , ранг матриці А дорівнюе 3.

1.4 Обернена матриця. Обернення (інвертування) матриць

Означення 3.22. Для кожної невироженої матриці А порядку n n існуе

одназначно визначена обернена матриця A 1 того самого порядку , така що

виконуеться рівність

A 1 A A A 1 En , (1.18)

En -одинична матриця порядку n.

Отже, умова невиродженості (несингулярності) матриці А є необхідною і

достатньою для існування оберненої матриці A 1. процес знаходження A 1 називають інвертуванням матриці А

А інвертування А-1

Таким чином , інвертуватись можуть тільки квадратні матриці, видзначник яких відмінний від нуля.

Теорема 1.1. Якщо видзначник (det A) не дорівнює нулю, то матриця А має обернену:

A 1

 

1

 

 

J,

 

 

A

 

 

 

 

 

 

 

 

 

 

де A -визначник матриці А; J-так звана приєднана до А матриця. Вона складається з алгебраїчних доповнень Aji до елементів aji матриці А, а саме:

 

 

A

A

A

 

A

 

 

 

11

21

31

 

n1

 

J

 

A12

A22

A32

An2

 

 

 

 

.

 

 

 

A2n

A3n

 

 

 

 

A1n

 

Ann

Отже,

 

 

 

 

 

 

 

 

 

A

A

A

 

A

 

 

 

 

 

 

 

 

 

 

 

11

21

31

 

n1

 

 

A

1

 

 

 

1

A12

A22

A32

An2

 

 

 

 

A

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A2n

A3n

 

 

 

 

 

 

 

 

 

 

 

 

A1n

 

Ann

 

Неведемо основні властивості оберненої матриці:

а)(AB) 1 B 1 A 1;

б) (ABC) 1 C 1B 1 A 1 ;

в)(A') 1 (A 1)';

г) A 1 1 ;

A

д) A 1 A E ;

1

A (Aij )'. (1.20)

12

е) E A 1 A A 1 A .

Дамо означення ще одного типу матриць. Якщо A 1 A', матрицю називають ортогональною.

Приклад 1.2. Знайти матрицю A 1, обернену до матриці А:

 

1

2

1

 

 

 

 

 

0

2

 

A

 

4 (див. підроздю 3.3).

A 3

.

 

 

4

2

5

 

 

 

 

 

 

 

 

 

Визначимо приєднану матрицю J:

 

A11

0

2

 

4; A12

3

2

 

7; A13

3

0

 

6;

 

 

 

2

5

4

5

 

4

2

 

 

A21

 

2

1

 

8; A22

 

 

1

1

 

9; A23

 

1

2

 

10;

 

 

 

 

 

 

 

 

 

2

5

 

 

4

5

 

 

 

 

4

2

 

 

A31

 

2

1

 

4; A32

 

1

1

 

5; A33

 

1

2

 

6;

 

 

 

 

 

 

 

 

 

0

2

 

 

3

2

 

 

3

0

 

Отже,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

8

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

J 7

 

 

 

 

5 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тоді

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

4

8

4

 

1

2 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7

 

9

 

 

 

 

 

 

5

 

 

 

 

 

A 1

 

 

7 9

5

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

4

4

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

6 10

6

3

5

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

2

Перевіремо, чи справді матриця

A 1 є

оберненою до матриці А. Знайдемо

A 1 Aабо

AA 1;

у результаті має бути одинична матрицю E. Отже, перевіряється

рівність A 1 A

AA 1=E:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 2

 

 

 

 

1 2

1

 

 

 

1 6 4

 

2 0 2

 

1 4 5

 

 

 

1 0 0

 

1

 

 

 

 

 

 

 

 

 

7

9

5

 

 

 

 

 

7

 

 

27

 

 

 

20

 

14

 

10

 

7

 

18

 

25

 

 

 

 

 

 

 

 

 

 

 

 

3 0

2

 

 

4

4

0

 

 

 

 

0 1 0 .

4

 

4

 

 

4

 

 

 

 

4

4

4

4

4

4

 

 

 

 

 

3

 

 

 

15

 

 

 

12

6

 

6

 

3

 

10

 

15

 

 

 

3

5

 

3 4 2

5

 

 

 

 

 

 

 

0

 

 

 

 

 

0 0 1

 

 

 

2

 

 

2

 

2

2

2

2

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.5.Блочні матриці. Дії з блочними матрицями

1.5.1.Визначення блочних матриць

Вцілому ряді випадків доцільно великі матриці розбивати вертикальними і горізонтальними прямими на кілька частин. Наприклад, нехай матриця А має порядок 5 6:

13

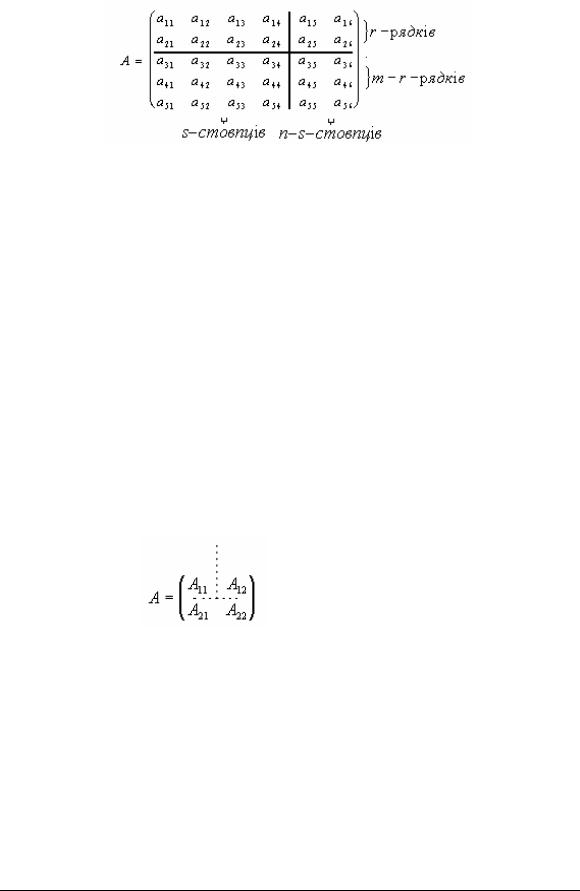
Розіб’ємо її на чотири матриці:

A

a11

a12

a13

 

a22

a23

11

a21

a

31

a

32

a

33

 

 

 

A21 a41

a42

a43

 

 

a52

a53

a51

Тоді матрицю А запишемо:

 

 

 

 

 

 

A

 

A

 

A

11

 

12

;

 

 

A21

 

A22

 

a14

 

A

a15

a16

 

a24

;

 

a26

;

 

12

a25

 

a

34

 

a

35

a

36

 

 

 

 

 

 

a44 ;

A22 a45

a46 ;

a54

 

 

 

a56

 

 

a55

 

 

 

 

(1.22)

 

 

Таким чином, маємо два різні записи однієї і тієї ж матриці А. В (1.22) матриця А складається з блоків елементів, або підматриць, тому таку матрицю часто називають блочною. Розбиття матриці роблять так, щоб підматриці, які стоять поруч (A11 A12 ; A21 A22 ), мали б рівну кількість рядків (відповідно r, m-r), а підматриці, які розмішені одна під одною(A11 A21; A12 A22 ),- рівну кількість стовпців, а саме: s; n-s (1.21).

1.5.2. Дії з блочними матрицями

а) Додавання матриць.

Нехай маємо блочні матриці А і В одного і того ж порядку та однаково розбиті:

.

Матриця C A B є також облочною матрицею того ж порядку, що й матриці А і В:

(1.23)

Таким чином, при додаванні (відмінні) блочних матриць насамперд має виконуватись умова,щб відповідні матриці-доданки мають однаковий порядок.

Зауважемо, якщо матриці розбиті таким чином, що можна виконати дію подібно тому, як це зроблено додаванні матриць А і В в (1.23), то таке розбиття має назву “відповідне”.

б) Множення матриць

Нехай А- матриця порядку m k ; а В – матриця порядку k n. У такому разі існує добуток С=АВ (див. рис. 1.1). Нехай матрицю А розбито на дві підматриці:

14

(1.24)

Другу матрицю Врозбито на дві підматриці B11 , B21:

(1.25)

Добуток двох матриць є матриця C AB A11B11 A12 B21, де A11 має порядок m s; B11 -s n;

A12 -m (k s); B21 (k s) n.

Нехай матриці А і В розбито відповідно на чотири підматриці:

Тоді відповідні підматриці мають розміри:

A11 r s;

A21 (m r) s;

A12 r (k s);

A22 (m r) (k s);

B11 s p;

B21 (k s) p;

B12 s (n p);

B22 (k s) (n p).

Добуток С=АВ складається з чотирьох підматриць C11,C12 ,C21,C22 ,

p-стовпців n-p-стовпців

Розміри підматриць відповідно дорівнюють:

C11 r p; C12 r (n p);

C21 (m r) p; C22 (m r) (n p).

Отже, рпи множенні блочних матриць має існувати відповідність між кількістю стовпців першої матриці А і кількістю рядків другої матриці В, тобто вони мають бути рівними.

Далі з блочними матрицями виконують операцію множення за тими самими правилами, що й зі звичайними матрицями.

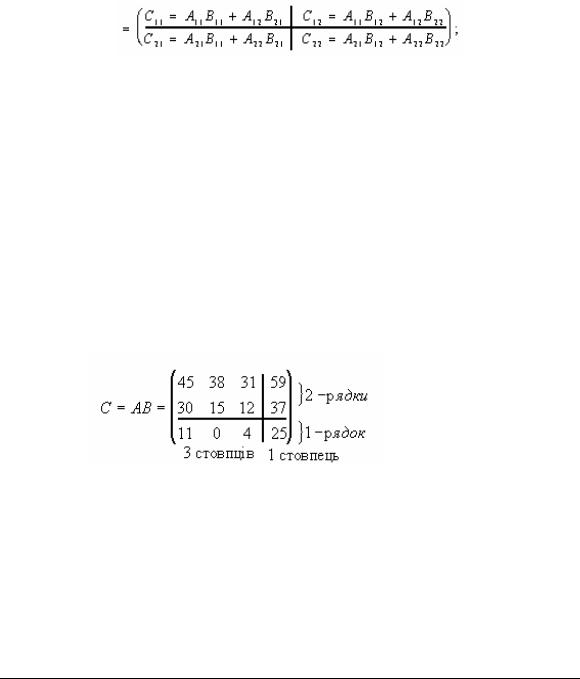
Приклад 1.3. Знайти добуток С=АВ двох матриць А і В :

15

A

 

1 3

4

; A

 

5

6

 

 

 

 

 

11

 

4 2

0

 

12

 

1

5

21

 

 

2 1

 

 

22

 

 

 

 

A

 

1 ; A

 

2 1 ;

Обчислюємо добуток С=АВ:

3 стовпці

 

1 стовпець

 

 

 

 

 

1

1

0

 

 

4

 

 

 

 

 

 

 

 

 

B11 2

0

2 ;B12 5 ;

 

 

 

1

5

 

 

 

 

 

 

 

1

 

 

1

B

 

2

1

3

;B

6

 

 

4

1

 

 

;

 

21

 

2

22

 

1

C

C

 

 

A

A

B

B

 

C 11

12

 

AB

11

12

11

12

 

C21

C22

 

 

A21

A22

B21

B22

 

 

 

1 3

 

1

 

1

0

 

 

5

 

6 2

1

 

3

 

11

 

 

21

10

34

17

21

45 38

31

C11

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

0 2

 

 

 

 

 

 

 

 

8 4 4

 

22 11 8

 

 

 

;

 

 

4 2

0

1

 

5

 

 

 

 

1 5 4

2 1

 

 

 

 

 

 

30 15 12

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 3

 

 

4

 

5

6 6

 

 

23

36

59

 

 

 

 

 

 

 

 

 

C12

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

4 2

 

 

5

1

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

5

1

 

 

26

 

11

37

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

21

 

 

 

 

1

3

 

4

 

 

2

 

1

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 3

4

 

 

 

C

 

1

4

 

2

 

 

 

2 1

4

 

 

1

 

 

 

8

3 8 11 0 4 ;

 

 

 

 

 

 

 

 

0

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

2

1

 

 

 

2

 

 

 

12 13 25.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

5

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Запишемо блочну матрицю-добуток С=АВ:

(1.26)

Отже, блочна матриця С=АВ має стільки рядків, скільки їх має блочна матриця А (m=3), і стільки стовпців, скільки їх має блочна матриця В (n=4).

Існує поняття прямого, або кронеккерового, добутку двох матриць. Якщо матриця А має порядок m n, а матриця В – розмір p q , то їх прямий добуток позначається

A B і обчислюється так:

 

a11B

a12 B

a1n B

 

 

a22 B

 

 

 

a21B

 

a2n B

A B=

 

 

 

.

 

 

an2 B

 

 

 

an1B

 

ann B

16

Порядок матриціA B є mp nq.

Приклад 1.4. Знайти рямий добуток A B, якщо:

2

3

1

 

 

 

 

1

3

 

 

A

2

;

 

 

 

 

B=

4

.

 

 

4

1

 

 

 

 

 

2

 

 

А має порядок 2 3; В- порядок 2 2; A B - порядок4 6.

 

 

 

 

 

 

2

6

3

9

1

3

 

2B

3B 1B

 

 

8 4

12

6

1

 

 

 

 

2

;

A B=

 

 

 

4

12

2

6

1

 

4B

2B 1B

 

 

3

 

 

 

 

 

 

8

8

4

4

 

 

 

 

 

 

16

2

 

Якщо матриці А та В двадратні й невироджені, також мають один і той самий розмір,

то справджується властивість: (A B)-1 =A-1 B-1 (на відміну від

(AB) 1 B 1 A 1).

Для блочної матриці

 

A

A

 

A

11

12

 

 

A21

A22

 

існує таке правило транспонування:

 

 

 

 

A'11

A'12

 

A'

 

A'22

;

A'21

 

множення блочної матриці на число виконується так:

A'11

A'12

 

A'

A'21

A'22

.

 

 

1.6. Обернення блочних матриць (формула Фробеніуса). Детермінант блочної матриці

НЕХАЙ А – НЕВИРОДЖЕНА МАТРИЦЯ, ЯКА Є БЛОЧНОЮ

 

A

A

 

A

11

12

.

 

A21

A22

 

Обернена до А матриця – також блочна, причому

 

 

 

(1.27)

Вираз (1.27) відомий в літературі як формула Фробеніса. Для оберненої матриці

A 1

виконується рівність: AA 1

A 1

E

0

 

A

, де E – одинична підматриця.

 

 

 

0

E

 

Запам’ятайте такий вираз:

 

 

 

 

 

(A BDB') 1 A 1 A 1B(B' A 1B D 1) 1 B' A 1,

(1.28)

17

де A і D – невироджені матриці відповідно розміру m n і n n; матриця В – порядку m n.

Детермінант (визначник) квадратної блочної матриці А визначається як

A

 

 

A11

A12

 

 

A

A

A 1

A

 

A

 

A

A

A 1

A

 

 

 

 

A

 

 

 

.(129.)

 

 

 

 

A21

A22

 

11

 

22

21

11

12

 

22

 

11

12

22

21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Нехай матриця А – невироджена і має блочно-діагональний вигляд:

A11

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A 1

 

0

(1.30)

A

0

,

 

 

 

 

 

 

 

 

 

 

 

A 1

11

 

 

A 1

,

 

A

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22

 

 

Визначник такої блочної матриці:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A

0

 

 

A

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

E

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Визначник блочно-діагональних матриць:

 

 

 

 

 

 

 

 

A11

0

 

 

 

 

 

A11

0

 

 

 

 

E

0

 

 

 

 

 

A

 

A

 

(1.31)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

A22

 

 

 

 

 

0

E

 

 

 

 

 

 

0

A22

 

 

 

11

 

22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A11

0

 

 

 

 

E

0

 

 

 

 

E

0

 

 

 

 

 

A11

 

 

A22

 

 

(1.32)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

A22

 

 

0

A22

 

 

0

A22

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.7. Системи лінійних рівнянь

ЗАПИШЕМО СИСТЕМУ РІВНЯНЬ У МАТРИЧНОМУ ВИГЛЯДІ

AX=D,

де

a11

a12

a13

a1, j

 

 

 

a22

a23

a2,j

a21

a

31

a

32

a

33

a

3,j

 

 

 

 

 

A

 

 

 

 

a

i1

a

i2

a

i3

a

ij

 

 

 

 

 

 

 

 

 

 

 

 

an2

an3

anj

an1

 

 

 

 

 

(1.32)

 

a1n

 

x

 

b

 

 

 

 

a2n

 

1

 

1

a

 

 

x2

b2

 

3n

 

 

 

 

; X =

;

B=

 

a

 

xj

bj

 

in

 

 

 

 

 

 

 

 

 

 

 

xn

bn

ann

 

 

 

 

Матриця А є квадратною порядку n; вектор-стовпець X має розмір n 1; вектор стовпець В – порядок n 1.

Якщо матриця А невироджена, тобто rgA=n і A 0, то система лінійних рівнянь

(1.32) має єдиний розвя’зок виду

 

 

 

 

X A 1B.

 

 

 

(1.33)

Приклад 1.5. Знайти розвя’зок системи

 

 

2x

3x

 

11;

 

1

 

2

2.

 

5x1 x2

У матричному виді:

AX=B;

18

 

 

 

 

 

 

 

 

2

3

 

 

x1

 

 

11

 

 

 

 

 

 

 

A

5

;

X

 

;

B

;

 

отже,

 

 

 

 

1

 

 

x2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

3 x

 

 

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

5 1 x2

 

2

 

 

 

 

 

A

 

=-2-15=-17 – матриця невироджена.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

b

 

 

 

 

 

 

 

 

 

Запам’ятайте: для матриці A

 

обернена матриця має вигляд

 

 

 

 

 

 

 

 

 

 

 

 

c

d

 

 

 

 

 

 

 

 

 

 

 

 

1 d

d

 

 

 

 

 

 

1

3

 

 

 

 

A 1

 

 

 

 

 

 

a

 

.

 

A 1

17

17

.

 

 

 

 

 

A

 

 

 

 

 

 

 

 

 

 

c

 

 

 

 

 

 

 

5

2

 

Отже,

 

 

 

 

 

 

 

 

 

 

 

 

 

17

17

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

3

 

11

 

1

 

 

 

 

 

 

 

 

 

 

X

17

 

17

.

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

5

 

2

 

 

 

2

 

3

 

 

 

 

 

 

 

 

 

 

 

 

17

 

 

 

 

 

 

 

Розв’язок системи : x1 1;x2

 

 

 

17

 

 

 

 

 

 

3.

 

 

 

 

 

 

 

 

 

 

Розглянемо однородну систему рівнянь:

 

 

 

 

 

 

 

 

 

 

 

AX=0.

 

 

 

 

 

 

 

 

 

 

 

(1.34)

Нехай A – квадратна матриця n-го порядку; X – вектор-стовпець розміру n 1.

Тривіальний розв’язок

 

має

вигляд:

x1 x2

xn 0. Нетривіальний розвязок

може існувати лише за умови, визначник матриці А дорівнює нулю:

A 0.

Коли це так, то система матиме безліч розвязків. Їх можна нормувати, вимагаючи, наприклад, щоб виконувалась рівність

n

 

 

xi2

1.

(1.35)

i 1

 

 

Приклад 1.6. Знайти нетривіальні розв’язки однорідної системи рівнянь.

x

1

2x

2

3x

3

0;

 

 

 

 

 

2x1

 

 

 

 

 

 

 

(1.36)

 

 

2x3

0;

 

 

 

 

 

 

 

 

2x3 0;

 

 

 

 

4x1 x2

 

 

 

 

 

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

3

x1

 

 

0

A 2

0

 

 

2 ;

X x2 ; B 0 .

 

 

 

4

1

 

 

 

 

 

 

 

 

 

 

 

 

2

x3

 

 

0

A 0, це означає, що задана система має нетнривіальні розв’язки. Матрицю А можна записати як систему трьох векторів:

 

1

 

2

 

3

 

 

 

 

 

 

 

A1 2 ;

A2 0 ;

A3 2 .

 

 

 

 

 

2

 

 

4

 

1

 

 

19

 

0

 

 

Систему (1.36) подамо як лінійну комбінацію вектора B

0 :

 

 

 

0

 

1

 

2

 

3

 

0

 

 

 

 

 

 

 

 

 

 

 

x1

2 +x2

 

0 +x3

 

2

= 0

(1.37)

 

 

 

 

 

2

 

 

 

 

 

4

 

1

 

 

 

0

 

Неважко побачити, що

x1

1; x2

2; x3

1; розв’язками системи (1.36) будуть і

ці самі значення, помножені на будь-які числа, які задовольняють рівняння (1.37).

Отже, система векторів A1, A2 , A3 є лінійно залежною, причому розв’язки системи

 

0

 

 

лінійних рівнянь (1.36) є коєфіціентами лінійної комбінації вектора

0 :

 

 

 

0

 

A1 2A2

A3 0.

 

 

 

 

(1.38)

1.8. характеристичні (власні) корені і власні вектори матриць

 

Розглянемо систему рівнянь

 

 

 

 

 

 

 

A X X,

 

 

 

 

(1.39)

 

де - скаляр: А – квадратна матриця порядку n, X – розміром n 1.

 

або

 

A X X 0,

 

 

(A E )X 0.

 

 

 

 

(1.40)

 

 

 

 

 

 

 

Остання система n рівнянь з n невідомими має нетривіальний розвязок, коли

 

det(A E ) 0 або

 

A E

 

0.

(1.41)

 

 

 

 

 

Означення

1.21.

Рівняння

 

det(A E ) 0відносно

називають

характеристичним рівнянням матриці А.

Корені цього рівняння є характеристичними коренями (характеристичними числами, власними значенями) матриці А.

Візмемо будь-який корінь k

характеристичного

рівняння (1.41) і підставимо в

систему рівнянь (1.40). Дістанемо рівняння

 

(A E k )X =0,

 

(1.42)

яке має нетривіальний розв’язок, оскільки det(A-E )=0/

Нехай цим розвязком є вектор

Xk . ТакиЙ вектор

Xk є характеристичним, або

власним, вектором матриці А, який відповідає характеристичному кореню k .

Якщо матриця А має n різних характеристичних коренів, то припускатимемо, що вона має і n різних власних векторів (задачі, які мають кратні характеристичні корені, в економіці зустрічаються рідко).

Власні вектори визначаються з точністю до множення на скаляр. Це нен завжди зручно. Тому розглядають нормовані власні вектори, тобто такі що:

Xi' Xi 1.

Зауважимо, що коли матриця А в рівняння (1.40) – симетрична (тобто А’=А), а X – матриця, кожний стовпець якої є власним вектором цієї матриці, то добуток

20

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности