
Сопромат 1_a_рус_2001
.pdf
|
|
|
|
|
|
|
|
|
|
|
21 |
2.3.7. Вычисляем величины моментов сопротивления относительно главных |
|||||||||||
центральных осей инерции: |
|
|
|
|
|
||||||
W1 |
|
|
I |
1 |
|
|
30311 |
14716,см3 |
|||
h |
|
|
|
206, |
|
||||||
|
|
1(max) |
|
|
|
|
|
||||
W2 |
|
I |
2 |
|
|
|
8819 |
|
7116,см3 |
||
h |
|
|
|
|
124, |
|
|||||
|
|
2(max) |
|
|
|
|
|
||||
h1max и h2max определяются с учетом масштаба из рисунка 2.6 . (Максимальные расстояния от соответствующей оси до наиболее удаленной точки сечения проводятся касательные к точкам сечения, параллельные соответствующей оси).
2.3.8. Проверки:
а). Инвариантность моментов инерции
Ix + Iy = I1 + I2
22596 + 16534 = 30311 + 8819
39130 = 39130
б). Эксперементальность моментов инерции:
I1 > Ix > Iy > I2
30311 >22596 >16534 > 8819
аналогично
I2 < Iy < Ix < I1
в).Перпендикулярность главных осей 1 и 2:
| 1| + | 2| = \2
36,79 + 53,21 = 90o = \2.

22
РАСЧЕТНО ПРОЕКТИРОВОЧНАЯ РАБОТА 3 Построение эпюр моментов и усилий при плоском изгибе в балках и раме.
Подбор поперечного сечения
3.1.Вопросы для самостоятельной работы.
3.1.1.Порядок определения и контроля реакций в статически-определимых балках.
3.1.2.Дайте определение численных значений изгибающего момента и поперечной силы в произвольном сечении балки.
3.1.3.Назовите и покажите правило знаков для Мх и Qy.
3.1.4.Какие Вы знаете дифференциальные зависимости между внутренними силовыми факторами при изгибе балок?
3.1.5.Каким образом проверить правильность построения эпюр Мх и Qy , их взаимное соответствие?
3.1.6.Как найти максимальное значение изгибающего момента на данном участке?
3.1.7.Почему на эпюре моментов в раме не указывается знак? С какой стороны строится эпюра Мх в рамах?
3.1.8.Условие прочности при изгибе.
3.2.Краткие теоретические сведения.
3.2.1.Границами участков на балке являются точки приложения сосредоточенных сил , моментов, а также точки начала и конца действия распределенной нагрузки.
3.2.2.Записывая аналитическое выражение Мх и Qy рассматриваем в равновесии часть балки, расположенную слева или с права, от сечения, полагая, что:
Изгибающий момент Мх в рассматриваемом сечении балки численно равен сумме моментов всех сил и пар сил, расположенных по одну сторону от сечения и взятых с определенным знаком.
Поперечная сила Qy в рассматриваемом сечении балки численно равна сумме проекций всех сил на ось, перпендикулярную оси балки, расположенных по одну сторону от сечения и взятых с определенным знаком.
3.2.3.Изгибающий момент считается положительным, если он вызывает растяжение нижних волокон балки. +Мх откладывается вниз (эпюра Мх строится на растянутых волокнах балки).
m
|
+M |
m |
|
-Mx |
|
|
x |
|
n |
|
|
|
n |
|
|
|
Поперечная сила считается положительной, если она вращает выделенный элемент по часовой стрелке.

|
23 |
m |
m |
+Qy |
-Qy |
n |
n |
3.2.4. Рекомендуется выбирать скользящую систему координат, т.е. начало координат помещать на правую или левую границу участка балки.
0 Zi l i.
3.2.5. Дифференциальные зависимости при изгибе:
dM |
x |
Q |
|
d2M |
x |
|
dQy |
q |
|
|
y |
|
|
|
|||
dz |
|
|
dz2 |
|
|
dz |
(z) |
|
|
|
|
|
|
|
Знак в правой части зависит от направления осей координат. 3.2.6. Условие прочности при изгибе:
max |
|
Mmax |
R Wx |
|
Mmax |
|
|
|
|||||
Wx |
R |
|||||
|
|
|
|
3.3.Порядок построения и проверка эпюр Мх и Qy в балках и рамах.
3.3.1.Проверить статическую определимость балки (рамы).
3.3.2.Определить опорные реакции и сделать проверку правильности вычислений.
3.3.3.Определить количество участков на балке (раме).
3.3.4.Записать для каждого участка аналитическое выражение Мх и Qy и найти значения в граничных точках. При необходимости сделать исследование функций Мх и Qy в пределах участка.
3.3.5.Построить с учетом размерности и знаков значений эпюры Мх и Qy.
3.3.6.Проверить соответствие эпюр Мх и Qy с учетом дифференциальных зависимостей.
3.3.7.Рамами называются системы, состоящие из прямолинейных стержней, соединенных узлами. Каждый прямолинейный участок рамы можно рассматривать как балку. Чтобы построить эпюру для рамы, нужно построить ее для каждой отдельной балки, входящей в состав рамы. В сечениях стержней рамы, кроме изгибающих моментов Мх и поперечных сил Qy, обычно действуют еще и продольные силы Nz.
Правила знаков для Мх, Qy, Nz остаются прежние. Эпюры строим на растянутых волокнах.
3.4. Содержание расчетной работы.
Для заданных балок, закрепленных и нагруженных как показано на рисунке, требуется:
1)определить опорные реакции;
2)построить эпюры поперечных сил и изгибающих моментов, определив их значения во всех характерных точках, При этом для каждого участка должны быть записаны аналитические выражения Мх и Qy с полным их исследованием. Варианты заданий
приведены в табл.3.1 3.6.
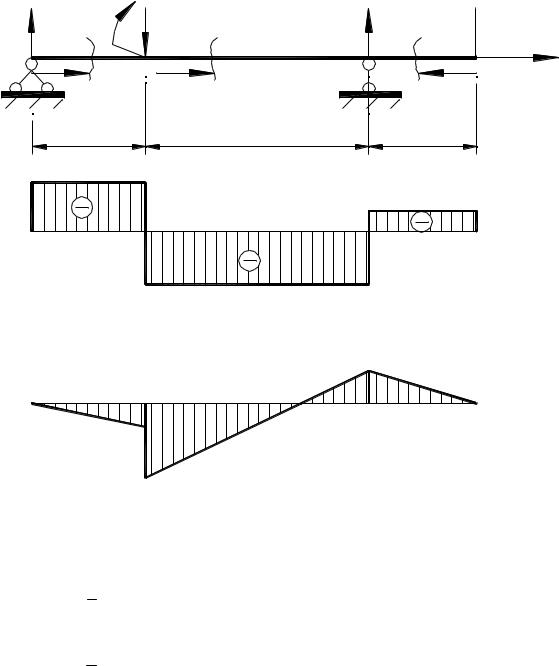
24
Пример выполнения расчетной работы.
Пример 3.4.1.
Построить эпюры Мх и Qy. Данные взять из Табл.3.1.
1. Проверяем статическую определимость балки. Для нахождения трех неизвестных реакций RA, Rc и Н имеем три уравнения статики 3 3=0.
Задача статически определима. 2. Определяем опорные реакции
RA |
M=6кНм |
RB |
P2 |
P1=18кН |
|||
A |
B |
C |
D |
z1 |
z2 |
|
z |
|
z3 |
||
1 |
2 |
|
1 |
9 |
9 |
3 |
3 |
|
|
||
|
|
|
Qy |
|
9 |
9 |
|
|
|
3 |
|
|
|
|
Mx |
9
15
Рис.3.1
Z=0, H=0,
MA =0; P1·1 Rc·3+P2·4+M=0
1
Rc 3 18 1 3 4 612kH
Mc=0; RA·3+M P1·2+P2·1=0
1
RA 3 6 18 2 31, 9kH
4. Проверяем найденные значения реакций:
Y=RA P1+Rc P2=9 18+12 3 = 0 .
Реакции найдены верно.
3. Балка имеет 3 участка: АИ, ВС, СD.
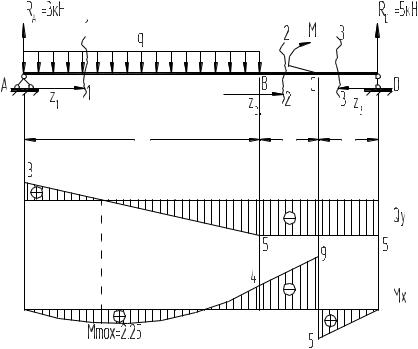
25
4. Записываем для каждого участка аналитические выражения для Мх и Qy. 1 участок 0 Z1 1
Qy =RA= 9 кН
MIx RA Z1; Mz=0 =0; Mz=1= 9·1 = 9кНм. II участок 0 Z2 2
Qy =RA P2= 9 18 = 9 кН
Mx= RA (1+Z2) P1Z2 +m; Mz=0 =15 кНм; Mz=2=3кНм. III участок
Qy = P2=3 кН
Mx = P2Z3; Mz=0 =0; Mz=1 = 3 кНм.
5.По найденным значениям Мх и Qy строим эпюры (см.рис.3.1).
6.Используем зависимость dМх / dz= Qy для анализа эпюр Мх и Qy:
эпюра Мх график функции;
эпюра Qy график первой производной функции.
На I и III участках производная Qy положительная функция возрастает, на II участке Qy = 9 кН, момент убывает от 15 кН до 3 кН.
На эпюре Мх скачек в сечении, где приложен сосредоточенный момент. На эпюре Qх скачки в сечениях, где действуют сосредоточенные нагрузки P1, RA, P2, Rс.
Пример 3.2.
4 |
1 |
1 |
|
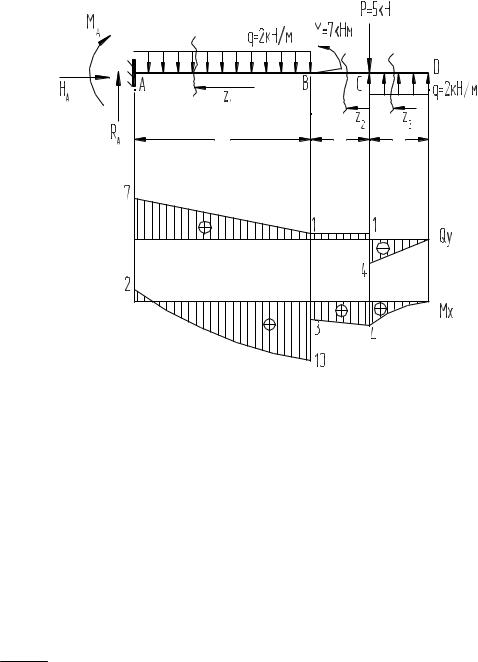
Рис.3.2 |
|
Построить эпюры Мх и Qy. Данные взять из рис.3.3. |
|
|
26
1. Проверяем статическую определимость балки. Для нахождения трех неизвестных RA, RD и Н имеем три уравнения статики: 3 3=0. Задача статически определима.
2. Находим величины опорных реакций;
МА=0; q·4·2+M RD·6=0; |
RD |
1 |
(2 4 2) 14 5кН. |
||
|
|
||||
|
6 |
|
|
||
MD=0; q·4·4 M RA·6=0; |
RA |
1 |
(2 4 4) 14 3кН. |
||
|
|||||
|
6 |
|
|||
Проверяем найденные значения опорных реакций:
Fy= RA q·4+ RD =5 8+3=0.
3.Балка имеет три участка.
4.Записываем аналитические выражения Мх и Qy для всех участков.
I участок 0 Z1 4
Qy =RA qZ1;
Qz1=0 =3 кН; Qz=4=3 8 = 5кН;
|
|
|
|
qZ2 |
|
|
|
|
|
|
|
2 42 |
|
|
Mx RAZ1 |
|
|
1 |
|
; Mz1=0=0; Mz 4 3 4 |
|
4кНм, |
|||||||
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|||
|
dMx |
RA qZ1 |
|
0 Z1 |
RA |
|
3 |
1,5м. |
|
|||||
|
|
|
q |
|
|
|||||||||
|
dZ1 |
|
|
|
2 1,52 |
|
2 |
|
|
|
||||
|
Mmax 3 1,5 |
2,25кНм. |
|
|
|
|||||||||
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
II участок 0 Z2 1 Qy = RD= 5 кН;
Mx= RA (4+Z2) q·4(2 +Z2); Mz=0 =3·4 2·4·2= 4 кНм; Mz=1=3·5 2·4·3= 9кНм.
III участок 0 Z3 1
Qy = RD= 5 кН;
Mx= RD Z3; Mz3=0 =0; Mz=1 = 5·1=5 кНм.
5.Строим эпюры Mx и Qy (рис.3.2).
6.На эпюре Qy скачки в точках А и D на величину реакций RA и RD. На эпюре Mx скачек в точке С на величину М = 14 кНм.
На первом участке при 0 Z 1,5, где Qy > 0 момент возрастает от 0 до 2,25 кНм. На всех остальных участках, где Qy < 0, функция момента убывающая.
Эти выводы справедливы для правосторонней системы координат.
27
Пример 3.3.
Для заданной консольной балки построить эпюры Mx и Qy и подобрать поперечное сечение в виде двутавра, двух швеллеров, прямоугольника (h=2b) и круга.
1. Проверяем статическую определимость заданной балки. Консольная балка статически определимая система, так как в защемлении возникают три неизвестных RA, H, MA, для нахождения которых имеются три уравнения статики: 3 3=0. Задача статически определима.
3 |
1 |
1 |
Рис.3.3. |
|
|
2.Реакции для консольной балки можно не определять и записывать выражения для Mx и Qy, рассматривая в равновесии правую отсеченную часть.
3.Балка имеет три участка.
4.Записываем аналитические выражения Mx и Qy для трех участков.
I участок 0 Z1 3
Qy = qZ1 +P q·2;
Qz1=0 =5 4=1кН; Qz=3=6+4 4 = 6кН;
Mz=0=7 5+8=10кНм; Mz=3= 9+7 20+20= 2кНм;
dMx |
qZ P q 2 0; |
Z1 |
|
P 2q |
|
5 2 2 |
0,5м. |
|
q |
|
|||||
dZ |
|
|
2 |
|
|||
Функция Мх не имеет экстремума на участке Z1= 0,5м < 0
d2Mx q (выпуклая)
dZ2
MZ1=1,5= 2,25+7 12,5+14=6,25кНм.

28
II участок 0 Z2 1 Qy=P q·2=5 4=1 кН; Mx= PZ2+q·2(1+Z2); Mz=0=4кНм; Mz=1= 5+8=3кНм. III участок 0 Z3 2
Qy = qZ3; Qz=0 =0; Qz=2= 4 кН;
Mx qZ32 ; Mz=0=0; Mz=2=4кН;
2
Mx |
qZ=0 q 0; |
d2Mx |
q. |
|
|
||
Z |
dZ2 |
||
5.По найденным значениям строим эпюры (рис.3.3).
6.На эпюре Мх скачек в точке В на величину сосредоточенного момента М=7 кНм. На эпюре Qу скачек в точке С на величину силы Р=5кН. На первом и втором участках эпюра Qy
>0, функция момента возрастает. На третьем участке Qy< 0, функция момента убывает от 4 кН до 0.
7.Подбираем поперечные сечения балок, исходя из условия прочности по нормальным напряжениям при изгибе.
W |
|
|
|
Mmax |
|
|
. Для балки Mmax= 10 кНм. |
||
|
|
||||||||
|
|
|
|
|
|||||
xтp |
|
|
|
|
R |
|
|||
|
|
|
|
|
|
||||
Wxтp |
103 |
|
|
|
476, 10 5 м3=47,6см3. |
||||
210 106 |
|||||||||
а) принимаем сечение двутавра № 12с Wx=58,4 см3, F=14,7см2
W |
][ |
|
Wxтp |
|
47,6 |
23,8 |
|
|
|
|
|||||
xтp |
2 |
2 |
|
см3 |
|||
в) сечение из двух швеллеров |
|
|
|||||
Принимаем 2 [ № 8 Wx=22,4·2=44,8см3 F = 2·8,98 = 17,96 см2;
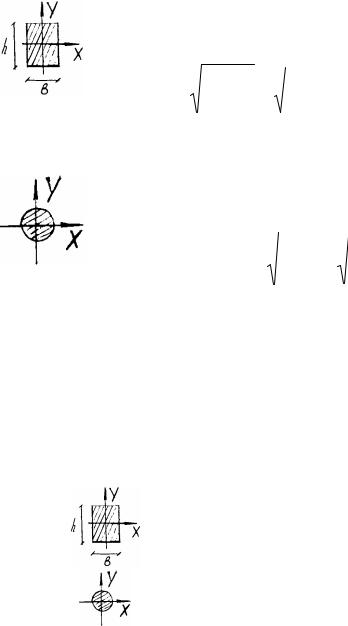
|
|
|
|
|
29 |
|
|
|
с) прямоугольное сечение (h=2b) |
|
|
|
|
||||
Wx |
|
bh2 |
|
b(2b)2 |
|
2b |
3 |
; |
|
|
|
|
|||||
|
6 |
6 |
3 |
|
|
|||
Wx=Wхтр; |
b 3 |
3Wxтр |
3 |
|
|
3 476, |
|
415,см; |
||||||||||||||
|
2 |
|
2 |
|
|
|
||||||||||||||||
h=2b 2·4,15=8,3см; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F=8,3·4,15=34,4см2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
d) круглое сечение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
r |
|
|
|
|
|
|
4W |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4 475, |
|||||||||||
W |
|
|
|
|
W |
|
; r = 3 |
|
|
x |
3 |
|
|
|
|
393,см; |
||||||
|
|
|
|
|
|
|
314, |
|||||||||||||||
|
x |
4 |
|
|
xтр |
|
|
|
|
|
|
|
|
|
||||||||
F = r2 = 3,14·3,932 = 49,2 см2
f) сравниваем балки с различными поперечными сечениями по массе длинной l = 1м и плотностью .
G1пм=V· = F l , l · const
Следовательно, достаточно сравнить балки по площади поперечного сечения. Результаты расчета сводим в табл.3.7
Таблица 3.7
№ п\п. |
Тип сечения |
Размер |
F, см2 |
% |
1 |
|
N № 12 |
14,7 |
100 |
2 |
] [ |
[ N № 8 |
18 |
122 |
3 |
|
h=8,3см |
34,4 |
234 |
|
b=4,15 см |
|||
|
|
|
|
|
|
|
|
|
|
4 |
|
r = 4см |
49,2 |
334 |
|
|
|
|
|
Наиболее рациональной является двутавровая балка.

30
Пример 3.4
Для рамы, изображенной на рис.3.5, построить эпюры Мх, Qy, Nz. 1. Проверяем статическую определимость рамы.
Данная рама является статически определимой, так как для нахождения трех опорных реакций RA, HA и RE имеем три уравнения статики: 3 3 = 0.
2. Определяем опорные реакции рамы:
Z = 0; HA+ P1 = 0; HA = P1 = 3 кН;МА = 0; P2· 2 + M P1 ·4 q·2·1+RE·2=0;
1
RE 2 3 4 2 2 4 2 2 3кН;
МЕ = 0; НА·4 М Р2 ·4 q·2·1+RA·2 = 0;
1
RA 2 2 4 4 2 2 3 4 5кН.
Проверка;
FY = RA q·2 P2+RE = 5 4 4+3 = 0. 3. Определяем количество участков:
Границами участков в рамах, кроме перечисленных в балках, являются узлы рамы. Данная рама имеет 4 участка.
4. Записывая выражения Мх, Qy, Nz для вертикальных элементов рамы, нужно условно стать лицом к этому элементу с любой стороны и рассуждать как в случае с балкой. Учитывая, что момент Мх при подходе с разных сторон имеет противоположные знаки, последние на эпюре Мх не указываются. Ординаты эпюр откладываются перпендикулярно оси рамы.
I участок 0 Z1 2;
Q4I RE qZ1; Z1 = 0; Q4I RE = 3кН;
Z1=2; Q4II 3 2 2 1кН;
I |
|
|
|
qZ12 |
|
I |
|
|
|
I |
|
2 22 |
|
Mx |
REZ1 |
|
|
; |
Mz 0 0; |
Mz 2 3 2 |
|
6 4 2кНм; |
|||||
|
2 |
||||||||||||
dMx |
|
2 |
|
|
|
RE |
|
3 |
|
|
|||
RE |
qZ1 0; Z1 |
|
|
1,5м; |
|
|
|||||||
dZ |
|
q |
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||
MIx(max) 3 1,5 2 1,52 4,5 2,25 2,25кНм.
2
d2Ma q; ( ) выпуклая
dZ2
Z = 0; Nz1 =0
IIучасток 0 Z2 3;
QII |
P |
3kH ; MII PZ |
2 |
R |
E |
2 q 2 1; |
|
y |
1 |
x |
1 |
|
|
||
MIIz 0 3 2 2 2 2кНм; MIIz 3 3 3 3 2 2 2 7кНм
