
Сопромат 1_a_рус_2001
.pdf
|
11 |
|
|
||
Полученное соотношение площадей: |
F1 |
|
|||
F :F |
0,7 |
0,265 отличается от заданного |
0,25. |
||
2,64 |
F |
||||
1 2 |
|
|
|||
|
|
|
2 |
|
|
Следовательно, учитывая, что 4F1 = F2, получим:
F1* 0,7см2 F2* 2,8см2 : 1 решение
F1* 0,66м2 F2* 2,65м2 : 2 решение.
Условию задачи удовлетворяет 1 решение, так как
F* F, a |
F* F . |
||
1 |
1 |
2 |
2 |
Определяем фактические напряжения в стержнях 1 и 2 с учетом принятых значений площадей:
F* 0,7см2 |
, |
F* |
2,8см2 |
1 |
|
2 |
|
|
|
|
|
= p M |
N |
1 |
|
M |
11,4 103 |
47,45 106 |
|
|
||||||||
|
|
|
F |
|
|
|
0,7 104 |
|
||||||||||||
|
|
|
1факт. |
|
|
1 |
|
1 |
* |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
210 106 a= 210 a= Rp |
|
|
|||||||||
|
|
= p t |
|
|
N |
1 |
t |
|
29,7 10 |
3 |
7,4 106 |
113,5 106 |
a= |
|||||||
|
|
F |
|
02,8 10 4 |
||||||||||||||||
|
2факт. |
|
2 |
2 |
|
|
* |
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
=113,5 a Rcm
12
РАСЧЕТНО-ПРОЕКТИРОВОЧНАЯ РАБОТА 2 Геометрические характеристики плоских сечений
2.1.Вопросы для самостоятельной работы.
2.1.Назовите геометрические характеристики плоских сечений и их размерности.
2.1.2.Какие оси инерции сечения называются:
центральными?
главными?
главными центральными?
2.1.3.Какой из двух моментов инерции Ix и Ixy может быть отрицательной величиной?
2.1.4.Как определяются моменты инерции фигуры относительно осей, не проходящих через центр тяжести фигуры?
2.1.5.Каким образом находится знак Ixy сечения из уголкового профиля без проведения математических вычислений?
2.1.6.Как определяются Iy, Ix, Ixy для сложного сечения?
2.1.7.По какой формуле определяется положение главных осей инерции?
2.1.8.В чем заключается свойство экстремальности главных осей инерции?
2.2.Краткие теоретические сведения.
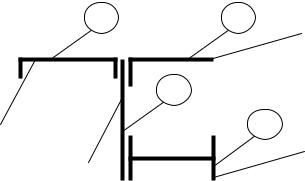
2.2.1. Оси проходящие через центр тяжести называются центральными.
Оси 1 и 2, относительно которых центробежный момент инерции I1,2=0, называются главными.
Главные оси, проходящие через центр тяжести сечения, называются главными центральными.
2.2.2.Моменты инерции относительно центральных осей инерции Ix0, Iy0 определяются по справочным данным, для прокатных профилей по таблицам сортамента.
2.2.3.Момент инерции сечения площадью F относительно произвольной оси, проходящей на расстоянии а от центральной оси Х0, определяется
Ix= Ixo + а2F.
2.2.4. Момент инерции сложной фигуры относительно оси равен сумме моментов инерции простых фигур, относительно этой оси:
Ix IxI IxII IxIII ...Ixn;
2.2.5. Положение главных осей инерции 1 и 2, проходящих через любую точку, определяется:
tg 1 |
|
Ixy |
|
, |
tg 2 |
|
Ixy |
|
; |
||
I |
y |
I |
1 |
I |
y |
I |
2 |
||||
|
|
|
|
|
|
|
|
||||
Ixу, Iу моменты инерции относительно осей Х и У, проходящие через эту точку; I1, I2 моменты инерции относительно главных осей 1 и 2.
13
2.3.Порядок выполнения работы.
2.3.1.Выписать из таблиц сортамента прокатной стали размеры и геометрические характеристики отдельных профилей. Для простых сечений аналитически определить
F1, Ix, Iy.
2.3.2.Вычертить на миллиметровой бумаге сечение в масштабе с указанием собственных центральных осей профилей, проходящих через центр тяжести и размеров, определяющих положение этих осей.
2.3.3.Выбрать вспомогательную систему координат и определить координаты центра тяжести всего сечения (Хс, Ус).
2.3.4.Вычислить осевые и центробежные моменты инерции всего сечения относительно
центральных осей, параллельных вспомогательным Ix, Iу, Ixу.
2.3.5.Определить величину главных центральных моментов инерции всего сечения I1 и I2.
2.3.6.Найти углы, определяющие положение главных центральных осей 1 и 2, которые показываются на чертеже.
2.3.7.Вычислите величину моментов сопротивления относительно главных центральных
осей W1 и W2.
2.3.8.Сделать необходимые проверки.
2.4.Содержание расчетной работы.
Для плоского сечения, составленного из прокатных профилей, требуется определить положение главных центральных осей и вычислить значения главных центральных моментов инерции сечения. Определить моменты сопротивления относительно главных осей.
Варианты заданий приведены в табл.2.1 и 2.3 (часть 1 б).
Пример выполнения расчетной работы.
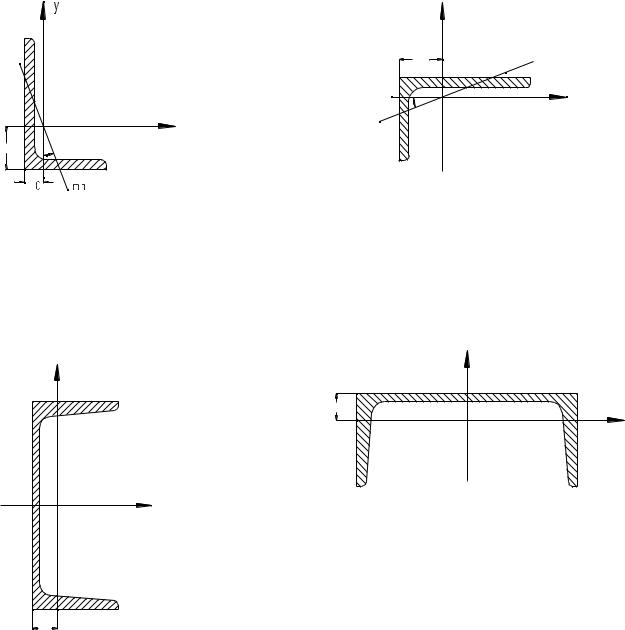
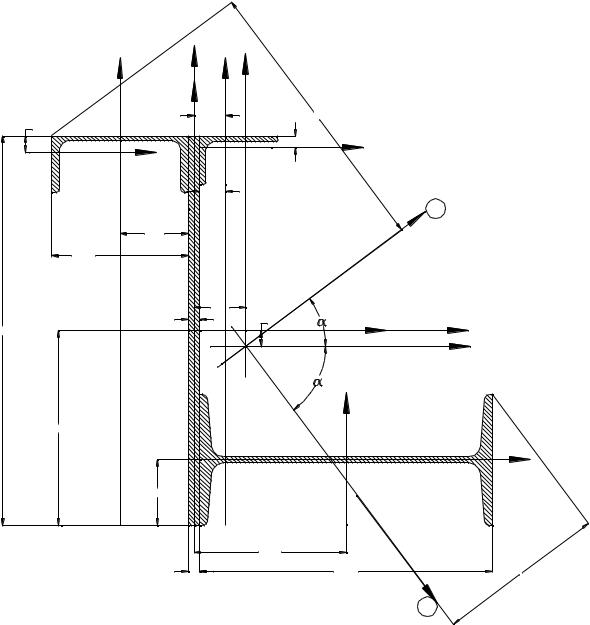
Дано сечение, состоящее из четырех профилей: листа 1, неравнобокого уголка 2, швеллера 3, двутавра 4. Схема сечения с номерами профилей приведена на рис.2.1 и 2.2.
3 2
L 80х50х6
1
4
№14
І №30
-- 400
Рис.2.1
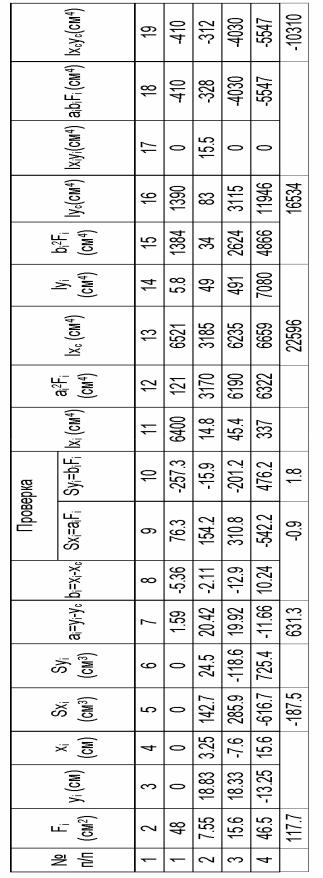
2.4.1 Выписываем из сортамента прокатных профилей необходимые размеры элементов (в сантиметрах) и величины геометрических характеристик сечения и заносим в таблицу исходных данных 2.4.
В случае, когда положение сечения в задании не соответствует расположению его в сортаменте, вносим изменения в величины геометрических характеристик.
14
Например:
а). Неравнобокий уголок: L 80х50х6
|
Сортамент |
|
0 |
|
C |
y0 |
x0 |
|
|
x |
U |
|
Рис.2.2а |
Ixo 49см4 Iуo = 14.8 см4
F = 7,55 см2 Х0 =2,65 см У0 = 1,17 см
Задание |
|
y0 |
|
x |
Umin |
0 |
|
y0 |
x0 |
C |
|
|
|
|
Рис.2.2.б |
|
|
Ix 14.8см4 |
F = 7,55 см2 |
||
o |
Х0 |
=2,65 см |
|
Iуo = 49 см4 |
|||
У0 |
= 1,17 см |
||
б). Швеллер: № 14 |
|
Сортамент |
Задание |
|
Ix |
491см4 |
|
|
y |
|
y0 |
o |
|
|
|
0 |
|
Iуo |
= 45.4 см4 |
|
|
|
|
|
|
x0 |
|
|
|
||
|
F = 15.6 см2 |
|
|
x0 |
||
|
Х0 =1.67 см |
|
|
C |
||
|
У0 = 0 см |
|
|
|
|
|
C |
x0 |
|
|
|
Рис.2.3.б |
|
|
|
|
Ix |
45.4 см4 |
F = 15.6 см2 |
|
|
|
|
o |
|
Х0 = 0 см |
|
|
|
|
Iуo = 491 см4 |
|
||
|
|
|
У0 = 1.67 см |
|
||
x0 |
|
|
|
|
|
|
Рис.2.3а |
|
|
|
|
|
|
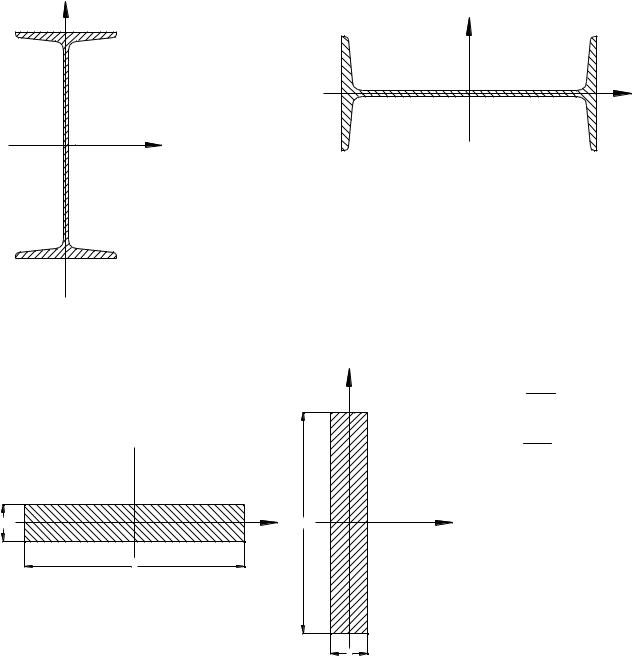
в). Двутавр: № 30 |
|
Сортамент |
|
y0 |
|
C |
x0 |
Рис.2.4а |
|
|
|
15 |
|
|
|
Ix |
|
7080см4 |
|
Задание |
|
|
|
|
|
||
o |
|
|
|
|
|
Iу |
o |
= 337 см4 |
|
y |
|
|
|
|
0 |
|
|
F = 46.5 см2 |
|
|
|
||
|
|
|
|
C |
x0 |
|
|
|
|
Рис.2.4.б |
|
|
|
Ix |
337 см4 |
F = 46.5 см2 |
|
|
|
o |
|
|
|
|
|
Iуo = 7080 см4 |
|
|
|
Моменты инерции полосы определяем как:
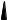 y0
y0
h |
x0 |
|
b |
|
y0 |
|
|
3 |
(2.1) |
|
Ix |
0 |
bh |
||
|
|
|
12 |
|
|
|
I |
y0 |
hb3 |
(2.2) |
|
|
|
12 |
|
||
h |
x0 |
|
|
|
|
|
b |
|
|
|
|
Рис.2.5 В таблице сортамента для неравнобокого уголка приведены значения минимального
момента инерции Imin и угла положения оси min, необходимые для определения центробежного момента инерции.
Величину Iy(max) для неравнобокого уголка находим из условия:
Ixo + Iуo = Iu + Iy = Imin+ Imax
Отсюда
Iy(max) = Ixo +Iуo Imin |
(2.3) |

16
2.3.2. Заданное поперечное сечение вычерчиваем в масштабе (рис.2.6).
Для каждого сечения показаны собственные центральные оси и размеры, определяющие положение центров тяжести отдельных профилей.
2.3.3. Определяем координаты центра тяжести всего сечения. В качестве вспомогательной системы координат Х1У1 примем оси, проходящие через центр тяжести листа Х0У0. При таком выборе вспомогательной системы вычисления несколько упрощаются.
Координаты центра тяжести сечения:
y |
|
|
Sxi |
|
|
F1Y1 |
F2Y2 F3Y3 F4Y4 |
, |
(2.4) |
|
c |
Fi |
|
|
F1 F2 F3 F4 |
||||||
|
|
|
|
|
|
|
|
|||
Xc |
Syi |
|
|
F1X1 F2 X2 F3X3 F4 X4 |
, |
|||||
Fi |
|
|
|
F1 F2 F3 F4 |
|
|||||
где Sxi, Syj статические моменты площади отдельных профилей; Xi, Yi координаты центров тяжести отдельных профилей во
вспомогательной системе координат. |
|
|
|
|||||
Из рис.2.6 найдем: |
|
|
|
|
||||
X1 = 0; |
|
|
X2 = 2,65 + 0,6 = 3,25 см, |
|||||
X3 = (7 + 0,6) = 7,6см; |
X4 = 15 + 0,6 = 15,6см; |
|||||||
Y 0; |
|
Y |
40 |
1,7 18,83см |
||||
|
|
|||||||
1 |
40 |
|
2 |
2 |
|
|||
Y |
|
18,33см. |
|
|
|
|||
|
|
|
1,67 |
|
|
|
||
|
|
|
|
|||||
3 |
2 |
|
|
|
|
|
||
Вычисления ведем в табличной форме (см. табл.2.5). Найденные значения координат заносим в столбцы 3,4 таблицы. В столбцах 5,6 вычисляются значения статических моментов отдельных профилей и всего сечения. По формулам (2.4) имеем:
Xc 631,3 5,37см 117,7
Yc 187,5 1,597 1,6см 117,7
|
|
17 |
|
|
|
y |
y0 |
y y |
|
|
|
3 |
y |
2 |
|
|
|
|
1 |
|
|
|
|
1.67 |
3.25 |
|
h1 |
|
|
|
1.17 |
|
|
|
|
|
x |
|
x0 |
|
|
C |
C |
|
|
||
3 |
2 |
|
|
|
|
3 |
|
|
|
|
|
|
2.65 |
|
|
|
1 |
|
|
|
|
|
|
|
7.00 |
|
|
|
|
14.00 |
|
|
|
|
|
|
5.37 |
|
x1 |
x0 |
|
40.00 |
1.20 |
1.6 |
1 |
||
C1 |
|
|
|
x |
|
|
C |
|
|
||
|
|
|
|
||
|
|
|
2 |
|
|
20.00 |
|
|
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
C |
x4 |
|
6.75 |
|
|
4 |
|
|
|
|
|
|
|
|
|
15.60 |
|
|
|
|
1.20 |
|
|
30.00 |
h2 |
|
|
|
|
|
2 |
|
Рис.2.6 (М 1:4) |
|
|
|
|
Таблица 2.4. |
|
|
|
|
|
Исходные данные задания. |
|
|
|
|
|
|
|
|
Центр тяжести |
|
|
|
|
|
|
|
№ |
Размеры |
F, |
собственных |
Ixo |
Iyo |
Imin |
Imax |
b |
tg |
|
п\п |
сечения |
см2 |
осей (см) |
см4 |
см4 |
см4 |
см4 |
см |
|
|
|
|
|
х0 |
у0 |
|
|
|
|
|
|
1 |
-40x1,2 |
48 |
|
|
6400 |
5,8 |
|
|
|
|
2 |
L8x5x0,6 |
7,55 |
2,55 |
1,17 |
14,8 |
49 |
54,92 |
54,92 |
|
0,386 |
3 |
[ № 14 |
15,6 |
|
1,67 |
45,4 |
49,1 |
|
|
5,8 |
|
4 |
] № 30 |
46,5 |
|
|
337 |
7080 |
|
|
13,5 |
|
18
Таблица 2.5
19
Наносим на рис.2.6 координаты центра тяжести С всего сечения и проводим через него центральные оси Х и У. Найдем координаты центра тяжести отдельных профилей в
новой системе координат: |
|
|
||||||||||||
|
|
|
|
|
|
|
ai |
= Yci Yc, bi |
= Xci Xc. |
(2.5) |
||||
Результаты этих вычислений заносим в столбцы 8,9 табл.2.5. |
|
|||||||||||||
Для проверки правильности вычислений координат центра тяжести необходимо |
||||||||||||||
вычислить статические моменты площади сечения относительно осей Х и У: |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
Sx aiFi , |
S4 bi Fi , |
(2.6) |
||
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
i 1 |
|
которые должны быть равны нулю. |
|
|
||||||||||||
Согласно столбцов 10, 11 табл.2.5 относительные погрешности равны: |
|
|||||||||||||
Sx |
|
|
|
|
|
0,9 |
|
|
|
100% 0,16% |
|
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
542,2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
S |
y |
|
|
|
1,8 |
|
100% 0,38% |
|
||||||
|
|
|
||||||||||||
|
|
|
|
476,2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
2.3.4. Вычислим осевые и центробежные моменты инерции всего сечения |
||||||||||||||
относительно центральных осей ХУ: |
|
|||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
||||
Ix Ixi0 ai2Fi , |
|
|
||||||||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
||||
|
|
|
4 |
|
bi2Fi , |
|
|
|||||||
Iy Iyi |
0 |
(2.7) |
|
|||||||||||
i 1
4
Ixy Iix0y0 a2i biFi , i 1
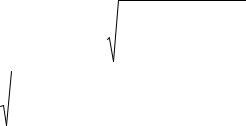
Вычисления по формулам (2.7) выполняются в столбцах 11 19 табл.2.5. Центробежный момент инерции уголка Ix2y2 вычисляется следующим образом. На
рис.2.7. показан уголок и его главные центральные оси U,V (2,1)
y2 |
|
|
|
|
Umin(1) |
C2 |
min |
x2 |
|
max |
|
|
Umax(2) |
|
Рис.2.7 |
|
|
20
Для неравнобокого и равнобокого уголков оси Х и У не являются главными, поэтому центробежный момент инерции для этих фигур определяем по формуле:
tg |
12, |
|
|
|
Ix |
o |
y |
o |
|
. |
(2.8) |
|||||||
I |
yo |
|
|
I |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
12, |
|
|
|
|
|||
|
|
|
|
|
|
I |
|
|
|
I , |
|
|
||||||
IL |
|
tg |
y |
(2.9) |
||||||||||||||
x y |
|
|
|
1 |
|
|
|
|
1 |
|
|
|||||||
|
o o |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
. |
|||
|
IL |
tg |
|
y |
I |
|||||||||||||
|
|
x y |
|
|
|
2 |
|
|
|
2 |
|
|||||||
|
|
|
o o |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Согласно рисунку 2.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 2 = tg = 0,386 |
|
|
||||||||||||||||
tg 1 tg(90o ) ctg |
|
|
|
1 |
|
|
1 |
2,59 |
||||||||||
|
|
tg |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
0,386 |
|
|||||||
IxL y |
o |
2,59(49 54,9) 15,3см4 |
||||||||||||||||
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IxLoyo = 0,386(49-8,9)=15,4см4
Для равнобокого уголка 1 = 2 = 45о, tg i = 1. Таким образом для всего сечения имеем (см.табл.2.4):
Ix = 22596 см4, Iy = 16534 см4, Ixy = 10310см4.
2.3.5. Вычислим главные центральные моменты инерции всего сечения:
|
I |
|
|
I |
x |
I |
y |
|
I |
x |
I |
y |
2 |
I |
2 |
|
22596 16534 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
12, |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
xy |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
22596 16534 2 |
10310 |
2 |
19565 10746, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
I1 = 30311см4, |
I2 = 8819см4 |
|||||||||||
Положение главных осей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
tg2 0 |
|
2Ixy |
|
|
2 ( 10310) |
|
34,, |
|
|
|
|
|
|||||||||||
Iy Ix |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
16500 22630 |
|
|
|
|
|
|
|
|||||||||||||
2 o=73,61o, o = 36,8o.
2.3.6. Определяем положение главных осей 1 и 2 относительно центральной оси Х:
tg 1 |
|
|
Ixy |
|
|
|
10310 |
3679,o |
||
Iy |
I1 |
|
|
|
||||||
|
|
16534 30311 |
|
|||||||
tg 2 |
|
Ixy |
|
10310 |
5321,o |
|||||
Iy |
I2 |
|
|
|||||||
|
|
|
|
16534 8819 |
|
|||||
o совпадает с углом 1.
Наносим с помощью транспортира главные оси 1 ( 1) и 2 ( 2) на рис.2.6.
