
- •Оглавление
- •2.Уравнения прямых и кривых на плоскости
- •3. Плоскость в пространстве
- •4.1.Матрицы. Операции над матрицами
- •4.2. Определители
- •4.3. Ранг матрицы
- •4.4. Обратная матрица
- •5.1. Критерий совместности Кронекера-Капелли
- •5.2. Метод Гаусса
- •5.3. Формулы Крамера
- •5.4. Матричный метод
- •5.5. Системы линейных уравнений общего вида
- •6.1. Предел последовательности и функции. Теоремы о пределах
- •7.1. Производная, правила и формулы дифференцирования
- •7.3. Экстремум функции
- •7.4. Раскрытие неопределенностей. Правило Лопиталя
- •7.5 Частные производные. Метод наименьших квадратов.
- •8.1. Основные методы интегрирования
- •Несобственные интегралы
- •9.1. Вероятность и риск, пространство элементарных событий
- •9.2. Независимость событий. Последовательные события и слепой случай. Теорема умножения вероятностей. "Дерево вероятностей"
- •9.3. Статистическое (частотное) определение вероятности. Теорема сложения вероятностей
- •9.4. Формула полной вероятности
- •9.5. Последовательтность испытаний (схема Бернулли)
- •10.1. Среднее арифметическое, мода и медиана. Среднее квадратическое отклонение
- •10.2. Нормальное распределение и его свойства
- •10.3. Выборки и доверительные интервалы
- •10.4. Центральная предельная теорема. Систематические изменения или случайность
- •10.5. Введение в корреляционный анализ. Основы регрессионного анализа
Несобственные интегралы
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:
![]() .
(8.7)
.
(8.7)
Если
этот предел существует и конечен, то
![]() называется
сходящимся
несобственным интегралом от
f(x)
на интервале [а,+),
а функцию f(x)
называют интегрируемой
на бесконечном промежутке [а,+).
В противном случае про интеграл
называется
сходящимся
несобственным интегралом от
f(x)
на интервале [а,+),
а функцию f(x)
называют интегрируемой
на бесконечном промежутке [а,+).
В противном случае про интеграл
![]() говорят,
что он не
существует, или расходится.
говорят,
что он не
существует, или расходится.
Аналогично определяются несобственные интегралы на интервалах (-, b] и (-, +):
![]() .
.
Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка [a,b], кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:
![]() ,
,
если эти пределы существуют и конечны. Обозначение:
![]() =
=
![]() .
(8.8)
.
(8.8)
Пример 3.29. Вычислить dx/(x+2).
Решение. Обозначим t=x+2, тогда dx=dt, dx/(x+2) = dt/t = lnt+C = = lnx+2+C.
Пример 3.30. Найти tg x dx.
Решение. tg x dx = sin x/cos x dx = - d(cos x)/ cos x. Пусть t=cos x, тогда tg x dx = - dt/t = - lnt+C = - lncos x+C.
Пример 3.31. Найти dx/sin x.
Решение.
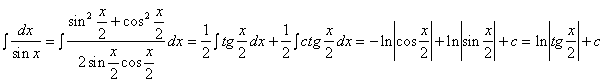
Пример
3.32.
Найти
![]() .
.
Решение.
![]() =
=
![]()
![]()
Пример 3.33. Найти arctg x dx.
Решение. Обозначим u=arctg x, dv=dx. Тогда du = dx/(x2+1), v=x, откуда arctg x dx = x arctg x - x dx/(x2+1) = x arctg x + 1/2 ln(x2+1) +C; так как x dx/(x2+1) = 1/2 d(x2+1)/(x2+1) = 1/2 ln(x2+1) +C.
Пример 3.34. Вычислить ln x dx.
Решение. Применяя формулу интегрирования по частям, получим: u=ln x, dv=dx, du= 1/x dx, v=x. Тогда ln x dx = x lnx - x 1/x dx = = x lnx - dx = x lnx - x + C.
Пример 3.35. Вычислить ex sin x dx.
Решение. Обозначим u = ex, dv = sin x dx, тогда du = ex dx, v= sin x dx= - cos x ex sin x dx = - ex cos x + ex cos x dx. Интеграл ex cos x dx также интегрируем по частям: u = ex, dv = cos x dx du=exdx, v=sin x. Имеем: ex cos x dx = ex sin x - ex sin x dx. Получили соотношение ex sin x dx = - ex cos x + ex sin x - ex sin x dx, откуда 2 ex sin x dx = - ex cos x + ex sin x + С.
Пример 3.36. Вычислить J = cos(ln x)dx/x.
Решение. Так как dx/x = d(ln x), то J= cos(ln x)d(ln x). Заменяя ln x через t, приходим к табличному интегралу J = cos t dt = sin t + C = sin(ln x) + C.
Пример
3.37.
Вычислить J =
![]() .
.
Решение.
Учитывая,
что
![]() =
d(ln
x),
производим подстановку ln
x
= t.
Тогда J =
=
d(ln
x),
производим подстановку ln
x
= t.
Тогда J =
![]() .
.
Пример
3.38.
Вычислить интеграл J =
![]() .
.
Решение.
Имеем:
![]() .
Поэтому
.
Поэтому
![]() =
=
=
=![]() =
=![]() .
.
Пример
3.39. Можно
ли применить формулу Ньютона-Лейбница
к интегралу
![]() ?
?
Решение.
Нет, нельзя.
Если формально вычислять этот интеграл
по формуле Ньютона-Лейбница, то получим
неверный результат. Действительно,
![]() =
=
![]() .
.
Но
подынтегральная функция f(x)
=
![]() >
0 и, следовательно, интеграл не может
равняться отрицательному числу. Суть
дела заключается в том, что подынтегральная
функция f(x)
=
>
0 и, следовательно, интеграл не может
равняться отрицательному числу. Суть
дела заключается в том, что подынтегральная
функция f(x)
=
![]() имеет
бесконечный разрыв в точке x
= 4, принадлежащей промежутку интегрирования.
Следовательно, здесь формула
Ньютона-Лейбница неприменима.
имеет
бесконечный разрыв в точке x
= 4, принадлежащей промежутку интегрирования.
Следовательно, здесь формула
Ньютона-Лейбница неприменима.
Пример
3.40.
Вычислить интеграл
![]() .
.
Решение.
Подынтегральная
функция определена и непрерывна при
всех значениях х
и, следовательно, имеет первообразную
F(x)=
![]() .
.
По
определению имеем:
![]() =
=
![]() .
.
По формуле Ньютона-Лейбница,
![]() =
F(b)
- F(0)
=
=
F(b)
- F(0)
=
![]() +
+![]() =
=
![]() ;
;
![]() =
=
![]() =
=
![]() .
.
Пример
3.44. (Из
экономики).
При анализе
непрерывных потоков платежей
предполагалось, что годовая сумма ренты
R равномерно распределяется на протяжении
года. На практике, особенно в инвестиционных
процессах, этот поток может существенно
изменяться во времени, следуя какому-либо
закону. Если этот поток непрерывен и
описывается некоторой функцией
R t
= f (t), то общая сумма поступлений за
время n
равна
![]() .
.
В этом случае наращенная по непрерывной ставке за период от 0 до n сумма составит:
S
=
![]() .
.
Современная величина такого потока равна
A
=
![]() .
.
Пусть функция потока платежей является линейной: Rt = Ro + at, где Ro - начальная величина платежа, выплачиваемого за единицу времени, в которой измеряется срок ренты. Вычислим современную величину A, пользуясь правилами интегрирования определенного интеграла:
A
=
![]() =
=
![]() +
+
![]() .
.
Обозначим
A1
=
![]() ,
A2
=
,
A2
=
![]() .
.
Имеем:
A1
=
![]() =
- Ro/
=
- Ro/![]()
![]() =
- Ro/(
=
- Ro/(![]() -eo)
= - Ro/(
-eo)
= - Ro/(![]() -1)
=
= Ro(
-1)
=
= Ro(![]() -1)/.
A2
=
-1)/.
A2
=
![]() .
Вычислим
неопределенный
интеграл
.
Вычислим
неопределенный
интеграл
![]() по
частям:
u = t, dv =
по
частям:
u = t, dv =
![]() dt
du = dt, v =
dt
du = dt, v =
![]() =
-
=
-
![]() /,
тогда
/,
тогда
![]() =
- t
=
- t![]() /
+ 1/
/
+ 1/
![]() =
- t
=
- t![]() /
(t+1/)
+C. Следовательно,
A2
= -a t
/
(t+1/)
+C. Следовательно,
A2
= -a t![]() /
(t+1/)
/
(t+1/)![]() =
((1-
=
((1-
![]() )/
- n
)/
- n![]() )a/.
)a/.
Итак, исходный интеграл
A=A1 +
A2=Ro(![]() -1)/+ ((1-
-1)/+ ((1-
![]() )/-n
)/-n![]() )a/.
)a/.
