Лекция 6
Тема: Моделирование подземных вод. Типы моделей подземных вод. Основные расчетные уравнения
Курс «Моделирование гидрологических процессов»
Некоторые определения
•Установившийся режим движения подземных вод – характеристики потока не изменяются по времени
•Неустановившийся режим движения подземных вод – характеристики потока изменяются по времени
•Закрытый водоносный горизонт – границы подземных вод неизменны по времени и пространству
•Открытый водоносный горизонт - границы подземных вод неизменны по времени и пространству, но поток имеет свободную поверхность
•Изотропная среда - характеристики среды в любой точке неизменны
•Анизотропной среда - характеристики среды изменяются в каждой точке
•Гетерогенная среда - условия изотропии или анизотропии меняются от точки к точке
•Гомогенная среда - условия изотропии или анизотропии неизменны
•Напорный поток - если все пустоты среды полностью заполнены жидкостью в направлении главного течения
•Безнапорный поток - если все пустоты среды неполностью заполнены жидкостью в направлении главного течения
Основные характеристики водоносного горизонта
Удельная водоотдача, которая определяет объем воды, отдаваемый в форме естественного стока или посредством откачки
Проницаемость, которая определяет скорость движения воды в водоносном горизонте
Пористость (a), которая определяет объем аккумулируемой влаги
a = 100w/V
w - объем воды, необходимый для заполнения или насыщения всего пористого пространства
V - общий объем почвы
Типы моделей подземных вод
Физические модели –представление процессов с помощью модели, включающей среду, через которую входит жидкость, контролируемая приборами для измерения давления и напора
Электрические модели - представление, в котором напор, поток и проводимость представлены напряжением, током и сопротивлением
Математические модели - представление, использующее набор алгоритмов для представления главных процессов
Стохастический анализ для характеристики моделирования подповерхностного стока и переноса
На практике чаще всего используется математическое и стохастическое моделирование
Главные составляющие математической модели подземных вод
Геометрия поверхностей, ограничивающих область расчета
Уравнения, которые описывают балансы компонентов, например массы жидкости, массы химических соединений и энергии
Уравнения потоков, которые связывают потоки компонентов c соответствующими переменными задачи
Уравнения состояния, которые определяют поведение конкретных фаз и соответствующих химических соединений, например, зависимость плотности и вязкости от давления, температуры и концентрации раствора
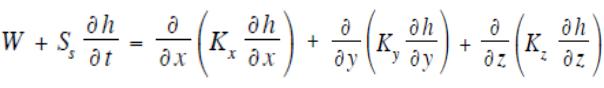
Уравнения, описывающие движение подземных вод
Движение подземных вод описывается системой из трех нелинейных дифференциальных уравнений в частных производных, выражающих:
- сохранение массы - уравнение неразрывности - уравнение сохранения количества движения
- уравнение состояния, связывающее между собой температуру, давление, объем и т.д.
Уравнение движения можно записать в виде
W - общая характеристика для источников и воронок Ss - удельное содержание влаги
h - пьезометрический напор
Kх, Ky и Kz - коэффициенты водопроводимости Kx = Ky = Kz = K - для изотропных сред
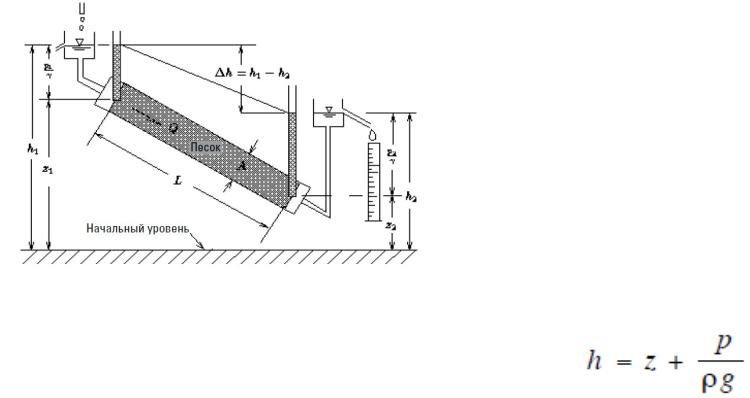
Закон Дарси
Рис. Эксперимент Дарси
V = K•A•dh/dL V - скорость потока
K - коэффициент проницаемости (иногда называемый гидравлической проводимостью)
dh/dL - гидравлический градиент или можно записать
V = K•A•(h1 – h2)/L
h - пьезометрический напор
z - высота точки, в которой рассматривается пьезометрический напор над некоторым исходным уровнем
p - давление жидкости ρ - плотность массы
g - ускорение свободного падения
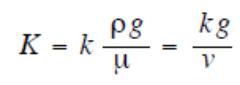
Расчет гидравлической проводимости
k - проницаемость или истинная водопроницаемость пористой среды
μ – динамический коэффициент вязкости
ν – кинематический коэффициент вязкости, определяемы по выражению ν = μ/ρ
Опции модели
Размерность модели (одно-, двух- или трехмерность)
Стационарный или нестационарный режим
Число и виды жидкостных фаз и соответствующий химический состав
Возможность фазовых переходов и химический обмен между смежными фазами
Режимы движения жидкости, например ламинарный или неламинарный
Соответствующие переменные состояния и площади или объемы, по которым следует проводить осреднение этих переменных
Модель - MODFLOW
MODFLOW - универсальный пакет программного обеспечения, разработанный Cлужбой геологии, геодезии и картографии США, который широко используется во всем мире в различных применениях
Модель MODFLOW имитирует движение подземных вод в пористой среде в трех измерениях, а также способна моделировать поток в двух измерениях
Область применения MODFLOW включает:
-стационарные и переходные потоки грунтовых вод
-движение подземных вод в ограниченных, в имеющих выход и неограниченных водоносных слоях
-некоторые особые проблемы потока, такие как родник и разгрузка в колодец
MODFLOW может быть использована при изучении взаимодействий между подземными и поверхностными водами, таких как частичная разгрузка подземных вод в реки и озера