
Лекция № 18
7.11. Определение потерь удельного импульса тяги в сопле
7.11.1. Потери из-за рассеяния
Формулу для расчета потерь удельного импульса тяги из-за рассеяния выводят с помощью теоремы импульсов для случая, когда поверхность перехода от дозвуковой к сверхзвуковой скорости течения плоская, а минимальное и критическое сечения сопла совпадают. Теорему записывают для объема РТ, ограниченного площадью минимального сечения сопла, боковой поверхностью расширяющейся части и площадью выходного сечения сопла.
В окончательном виде формула записывается
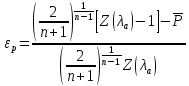 ,
(217)
,
(217)
где
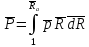 -
безразмерный интеграл сил давления,
-
безразмерный интеграл сил давления,
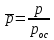 ,
,
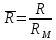 - относительный радиус сопла в сечении
х,
а
- относительный радиус сопла в сечении
х,
а
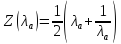 – газодинамическая функция потока.
– газодинамическая функция потока.
Зависимость
от
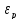
п,
характеризующего состав рабочего тела,
не сильная . даже при увеличении п
от 1.14 до 1.40
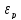 возрастает всего на 0.005...0.010.
возрастает всего на 0.005...0.010.
Для конических сопел при условии радиального течения в них РТ получена следующая формула для расчета потерь удельного импульса из-за рассеяния
 ,
(218)
,
(218)
где
 — полуугол расширяющейся части
конического сопла.
— полуугол расширяющейся части
конического сопла.
Потери,
вычисленные по выражению (218), согласуются
с расчетами осесимметричных течений
с точностью 10…20% при
 < 3 %.
< 3 %.
В первом приближении оценку потерь удельного импульса из-за рассеяния в профилированных соплах Лаваля можно проводить по формуле
 ,
(219)
,
(219)
где
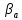 - угол касательной к контуру сопла в
выходном сечении (на срезе) с осью.
- угол касательной к контуру сопла в
выходном сечении (на срезе) с осью.
Возникают
дополнительные потери из-за рассеяния,
вызванные неравномерным распределением
параметров РТ в минимальном сечении
сопла. Если скругление угловой точки А
производится радиусом
 ,
то при
,
то при
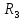 <
<
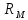 дополнительные потери удельного
импульса может приближенно определить
по эмпирической зависимости
дополнительные потери удельного
импульса может приближенно определить
по эмпирической зависимости
 .
(203)
.
(203)
Тогда
 .
.
Потери
удельного импульса из-за рассеяния в
соплах современных РД составляют
0.010...0.015 (1,0...1,5 %), а дополнительные потери
 при 0,5 <
при 0,5 <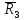
<
1,0 не превышают 0,002 (0.2 %).
7.11.2 Потери из-за трения
При течении вязких продуктов сгорания по соплу возникают силы трения, стремящиеся увлечь стенку в направлении потока, т.е. направленные в противоположную тяге сторону и снижающие ее.
Величина потерь удельного импульса из-за трения может быть определена по формуле, вывод которой приводится в учебнике В.Е. Алемасова «Теория ракетных двигателей»,
 (221)
(221)
где

=
- относительная толщина потери импульса,
а

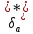
—
толщина потери импульса, Ма
- число Маха на выходе из сопла,
определяемое по результатам расчета
одномерного течения.
В пограничном слое сопел возможны ламинарный, турбулентный или переходный режимы течения. Режим течения определяется характерным числом Рейнольдса
 ,
(222)
,
(222)
где
 - максимальная скорость истечения РТ,
- максимальная скорость истечения РТ,
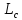 — полная длинна сопла,
— полная длинна сопла,
 — динамическая вязкость.
— динамическая вязкость.
Максимальная скорость истечения рабочего тела

Значение критического числа Рейнольдса, при котором происходит перестройка режима течения, зависит в основном от следующих факторов:
^
числа Маха М
потока;

4 6 8 10 12 14 16

Рис.
32. Зависимость потерь из-за трения в
расширяющейся части сопла от

^
фактора теплообмена
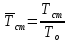 ;
;
^
степени шероховатости сопла;
^
градиента давления.
Экспериментально
установлено, что при числах Рейнольдса
 < 107
пограничный слой является ламинарным,
при
< 107
пограничный слой является ламинарным,
при
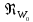 > 3 107
турбулентным, а в интервале
> 3 107
турбулентным, а в интервале
 = 107...3
107
переходным.
= 107...3
107
переходным.
В соплах РД возможны все режимы течения в пограничном слое. В соплах РДМТ обычно имеет место ламинарный режим течения, а в соплах двигателей больших тяг - турбулентный.
Изобразим
на рис. 32 зависимость потерь удельного
импульса тяги из-за трения в расширяющейся
части сопла
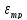 от относи-
от относи-
тельной
длины сверхзвуковой части сопла
 при турбулентном режиме течения в
пограничном слое (
при турбулентном режиме течения в
пограничном слое (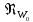 = 108).
= 108).
Потери
удельного импульса тяги из-за трения
 увеличиваются с ростом длины сопла.
увеличиваются с ростом длины сопла.
Для
фиксированного сопла потери из-за трения
увеличиваются с уменьшением фактора
теплообмена Тст
и среднего показателя изоэнтропы п.
Это связано с увеличением плотности РТ
вблизи стенок сопла и влиянием отвода
тепла на

.
Потери
из-за трения в соплах современных РД
составляют
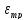 = 0,01...0,03.
= 0,01...0,03.
В
некоторых случаях внутреннюю поверхность
сопла полируют, чтобы снизить шероховатость.
Это позволяет уменьшить потери из- за
трения
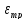 до 0,0075.0,0150.
до 0,0075.0,0150.
