Жазық-параллель қозғалыстағы дене нүктелерінің жылдамдығы

Жылдамдығы белгілі А нүктені полюс етіп алып, жазық қиманың өз жазықтығындағы қозғалысын қарастырайық (3-сурет).

А мен В нүктелерінің және радиус-векторларын жүргізіп, А-дан В-ға жүргізілген векторды арқылы белгілейік. Сонда суреттен:

. (2)

Енді (2) теңдеуінен уақыт бойынша бірінші туынды аламыз:

. (3)

Жазық қима қозғалған кезде векторының модулі тұрақты, ал бағыты өзгеретін болғандықтан осы вектордан уақыт бойынша алынған туынды В нүктесінің А полюсін айналғандағы жылдамдығының векторы болады. Бұл жылдамдықты деп белгілеп, оны анықтайтын өрнек аламыз:

. (4)

Бұл вектор АВ-ға перпендикуляр w-ның бағытымен бағытталған, ал оның сан шамасының өрнегі:

. (5)

А мен В нүктелерінің радиус-векторларының туындылары осы нүкте жылдамдықтарының векторлары екенін ескерсек:

,

онда жазық қозғалыстағы дене нүктелерінің жылдамдықтарын қосу туралы теореманы аламыз: жазық қиманың кез келген В нүктесінің жылдамдығы А полюстің жылдамдығы мен осы нүктенің полюсті айналғандағы жылдамдығының геометриялық қосындысына тең:

. (6)

векторының сан шамасы мен бағытын параллелограмм тұрғызу арқылы анықтауға болады (4 сурет).

Жазық қиманың екі нүктесі жылдамдықтарының проекциялары туралы теорема

Жазық қима нүктелерінің жылдамдығын (6) өрнегінің көмегімен тікелей анықтау әдетте күрделі есептеулерді немесе күрделі тұрғызуларды талап етеді. Алайда қима нүктелерінің жылдамдығын осы өрнектің көмегімен қарапайым әдіспен анықтауға болады. Осындай әдістің біріне келесі теорема жатады.

Теорема. Жазық қиманың екі нүктесінің жылдамдықтарының осы нүктелер арқылы өтетін түзуге проекциялары өзара тең.

Д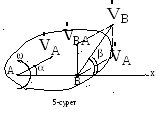әлелдеу. Берілген уақытта жазық қиманың А нүктесінің жылдамдығы , бұрыштық жылдамдығының айналу бағыты мен  модулі белгілі болсын (5-сурет). В нүктенің жылдамдығы (6) өрнегімен анықталады. Енді А және В нүктелері арқылы х өсін жүргізіп, (6) өрнегін осы өске проекциялаймыз:

, (7)

векторы х өсіне перпендикуляр болғандықтан , болады.

Сонымен (7) өрнегінен мынаны аламыз:

немесе . (8)

Жылдамдықтардың лездік центрі (ЖЛЦ)

Жазық қима нүктелерінің жылдамдығын анықтаудың басқа көрнекті әдісі жылдамдықтардың лездік центрі ұғымына негізделген.

Жазық қиманың берілген уақытта жылдамдығы нөлге тең нүктесі жылдамдықтардың лездік центрі (ЖЛЦ) деп аталады.

Теорема. Егер жазық қиманың бұрыштық жылдамдығы нөлге тең болмаса , онда жылдамдықтардың лездік центрі бар.

Дәлелдеу. А нүктесінің жылдамдығы нөлге тең емес болсын . Нөлге тең болса бұл нүкте анықтама бойынша жылдамдықтардың лездік центрі болуы керек. А нүктесінен бұрыштық жылдамдықтың бағытына қарай оның жылдамдығына перпендикуляр етіп кесіндісін жүргіземіз (2.21 сурет). Дене нүктелерінің жылдамдықтарын қосу туралы (6) теоремаға сәйкес былай жазуға болады:

. (9)

жылдамдығы  -ның бағытымен АР-ға перпендикуляр бағытталған (2.21 сурет), оның сан шамасы .

екенін ескерсек:

. (10)

Сонымен, мен жылдамдықтарының сан шамалары тең, ал бағыттары қарсы болып шықты, яғни олардың геометриялық қосындысы:

.

Демек Р нүктесі жылдамдықтардың лездік центрі болады екен.

Жылдамдықтардың лездік центрінің көмегімен жазық қиманың кез келген нүктесінің жылдамдығы мен қиманың бұрыштық жылдамдығын анықтайтын өрнектер алуға болады. Ол үшін жылдамдықтардың лездік центрін полюс етіп алып, В нүктесі үшін (2.4.6) теореманы жазамыз (6-сурет):

,

бірақ , сондықтан

ал

Сонымен, В нүктісінің жылдамдығының модулі:

, (11)

ал жылдамдық векторы ВР-ға перпендикуляр w-ның бағытымен бағытталады (6-сурет).

Дәл осылай С нүктесі үшін де , яғни:

(12)

бұл жылдамдықтың векторы СР-ға перпендикуляр w-ның бағытымен бағытталады (6-сурет).

(10) – (12) өрнектерінен мынаны аламыз:

. (13)

Сонымен, жазық қиманың кез келген нүктесінің жылдамдығы нүктеден ЖЛЦ-іне дейінгі ара қашықтыққа пропорционал, ал нүкте жылдамдығының векторы осы нүктені ЖЛЦ-імен қосатын кесіндіге (лездік радиусқа) перпендикуляр бағытталады.