1.2.3 Үш күш туралы теорема

Теорема. Егер өзара параллель емес үш күш әсер ететін дене тепе-теңдікте болса, онда күштердің үшеуі де бір жазықтықта жатады және олардың әсер ету сызықтары бір нүктеде қиылысады.

Өзіндік бақылау сұрақтары:

1. Жинақталатын күштер жүйесінің анықтамасы.

2. Жинақталатын күштер жүйесінің тең әсерлі күшін анықтау.

3. Жинақталатын күштер жүйесінің тепе-теңдік шарттары.

4. Өзара параллель емес үш күш туралы теорема.

1.3 Моменттер теориясы

1.3.1 Күштің нүктеге (центрге) қатысты моментінің векторы

Күштің әсерінен қатты дене ілгерілемелі немесе айналмалы қозғалыс жасайды. Күштің айналдырушы әсері моментпен сипатталады.

күшінің О нүктесіне (центріне) қатысты моменті деп осы нүктеге түсірілген векторын айтады. Бұл вектордың модулі (шамасы) күш модулі мен күштің нүктеге қатысты иінінің көбейтіндісіне тең, ал бағыты күш пен нүкте арқылы өтетін күш жазықтығына перпендикуляр, оның ұшынан қарағанда күш денені сағат тіліне қарсы бағытта бұратындай болып көрінеді (1.13 сурет).

Күштің О нүктесіне қатысты моментінің шамасы (модулі):

. (1.3.1)

Күштің нүктеге қатысты иіні (h) деп нүктеден күштің әсер ету сызығына дейінгі ең жақын ара қашықтықты (перпендикулярды) айтады.

Күштің О нүктесіне қатысты моментінің векторын күштің түсу нүктесінің радиус-векторы мен күш векторының векторлық көбейтіндісі ретінде жазуға болады:

. (1.3.2)

Екі вектордың векторлық көбейтіндісін анықтауыш түрінде алып, векторының декарттық координата өстеріне проекцияларын анықтаймыз:

.

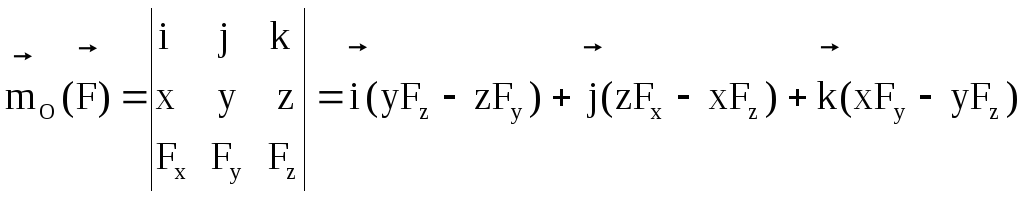күшінің О нүктесіне қатысты моменті векторының проекциялары мына түрде жазылады:

(1.3.3)

Халықаралық жүйеде күш моменті ньютон көбейтілген метрмен өлшенеді. 

1.3.2 Қос күш және оның моментінің векторы

Қос күш деп модульдері тең, бір біріне қарсы бағытталған екі параллель күштің жүйесін айтады. Қос күштің әсерінен дене айналмалы қозғалыс жасайды, демек, қос күштің моменті болады. Қос күш жатқан жазықтыққос күштің әсер ету жазықтығы деп аталады. Қос күшті құрайтын күштердің әсер ету сызықтарының арасындағы ең жақын ара қашықтық (перпендикуляр) қос күштің иіні (d) деп аталады (1.14 сурет).

Енді жазықтығында жатқанқос күшті қарастырайық. Осы екі күштің кез келген О нүктеге қатысты моменттерінің геометриялық қосындысын алайық:

Егер екенін ескерсек мынаны аламыз

.

Алынған өрнек қос күш моментінің векторы деп аталады, ол О нүктесіне тәуелсіз:

. (1.3.4)

Қос күш моментінің модулі оны құрайтын күштердің біреуінің модулі мен қос күш иінінің көбейтіндісіне тең:

.

Қос күш моменті векторының бағыты қос күштің әсер ету жазықтығына перпендикуляр, ұшынан қарағанда қос күш денені сағат тіліне қарсы бағытта бұратындай болып көрінеді. Оны кез келген нүктеге түсіруге болады, себебі ол О нүктесіне тәуелсіз, яғни қос күш моментінің векторы – жылжымалы вектор.