1.8 Ауырлық центрі

1.8.1 Параллель күштер центрі

() параллель күштер жүйесін қарастырайық (1.31 сурет). Олардың тең әсерлі күші:

. (1.8.1)

Енді осы күштерді олардың түсу нүктесі төңірегінде бір бағытта және бірдей бұрышқа бұрайық. Алынған күштер жүйесі модульдері мен түсу нүктелері өзгермеген параллель күштер жүйесі болады. Осындай күштер жүйесінің әрқайсысының тең әсерлі күшінің модулі бұрынғыдай, ал бағыты әртүрлі. Күштер жүйесін кез келген жаққа бұрғанда тең әсерлі күштің әсер ету сызығы бір С нүктесі арқылы өтетін болады. Осы нүктепараллель күштер центрі деп аталады.

Осы нүктенің радиус-векторын табайық. Ол үшін Вариньон теоремасын қолданамыз. күштер жүйесінің тең әсерлі күші болғандықтан,теорема бойынша оның кез келген нүктеге қатысты моменті барлық күштердің сол нүктеге қатысты моменттерінің қосындысына тең. Момент алынатын нүкте етіп С нүктесін алайық. Сонда

. (1.8.2)

күші С нүктесінен өтетін болғандықтан оның осы нүктеге қатысты моменті нөлге тең, ал (1.3.2) теңдеуін қолданып екенін аламыз, сонда (1.8.2) теңдеуі былай жазылады:

. (1.8.3)

1.31 суреттен екенін көреміз. Берілген күштерге параллель етіпбірлік векторын ендірейік. Сонда кез келген күш векторын былай жаза аламыз:

егер менвекторлары бағыттас болса, бұл жердегі, ал егермен

векторлары қарсы бағытта болса, онда . Осы айтылғанды ескеріп (1.8.3) теңдеуін былай жазамыз:

Осыдан параллель күштер центрінің радиус-векторы өрнегін аламыз:

(1.8.4)

мұндағы -күшінің түсу нүктесінің радиус-векторы, алкүші бағытына қарай не-ға, не ()-ға тең болады.

Сонда параллель күштер центрінің координаталары мынандай болады:

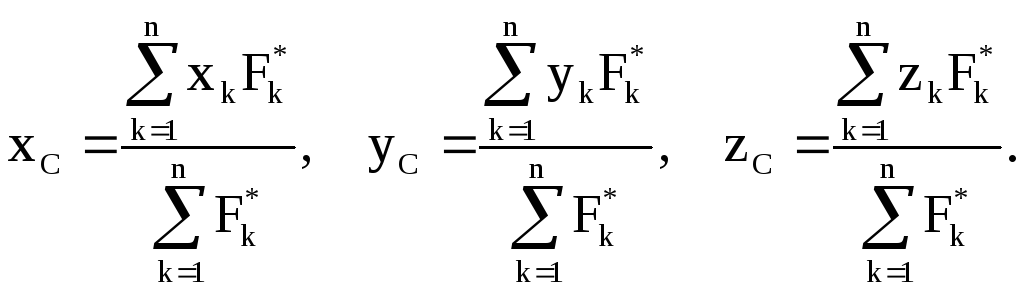(1.8.5)

1.8.2 Қатты дененің ауырлық центрі

Жер бетіне жақын орналасқан дененің әр нүктесіне жердің центріне қарай вертикаль төмен бағытталған ауырлық күші әсер етеді (1.32 сурет). Егер дене өлшемдері жер өлшемдерінен әлдеқайда кіші болса, онда бұл күштерді шамалары тұрақты және бір біріне параллель деп есептеуге болады.

Берілген дене нүктелеріне әсер ететін ауырлық күштердің тең әсерлісін деп белгілейік. Осы күштің модулі дененің салмағы болады. Денені қалай қарай бұрсақ та күштері бір біріне параллель және бір нүктеге түсірілген болып қала береді. Демек, осы күштердің тең әсерлі күші , параллель күштер жүйесінің тең әсерлісі ретінде әрқашан бір нүктеден ғана өтетін болады. Дененің ауырлық центрі деп оның барлық нүктелерінің ауырлық күштерін құратын параллель күштер жүйесінің центрін атайды. Дененің ауырлық центрінің радиус-векторын және координаталарын (1.8.4) пен (1.8.5) теңдеулеріне сәйкес мына өрнектермен анықтауға болады:

(1.8.6)

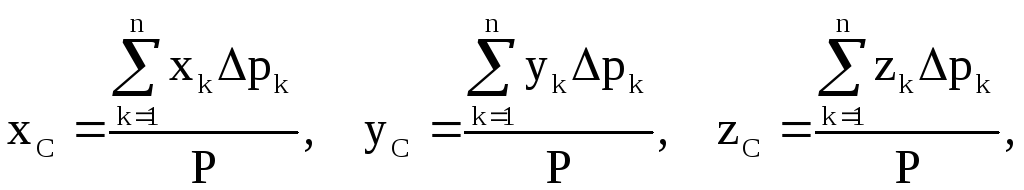(1.8.7)

мұндағы – нүктелердің радиус-векторлары мен координаталары, – нүктелердің салмақтары, ал Р – бүкіл дененің салмағы.

Егер денені жеке нүктелерге бөлуге болмаса (тұтас орта немесе континуум болса), онда денені элементар көлемдерге бөледі. Осындай көлемнің әрқайсысының салмағы көлемге пропорционал , ал дененің салмағы осы дененің көлеміне пропорционал, яғни ,мұндағы - элементар көлемнің меншікті салмағы. Біртекті дене үшін - тұрақты шама болғандықтан, мен -ның мәндерін (1.8.7) теңдігіне қойсақ, қосындылардағы ортақ көбейгіш ретінде жақшаның сыртына шығарылып, бөлімдегі -мен қысқарады. Нәтижесінде, біртекті көлемнің ауырлық центрінің координаталарын аламыз:

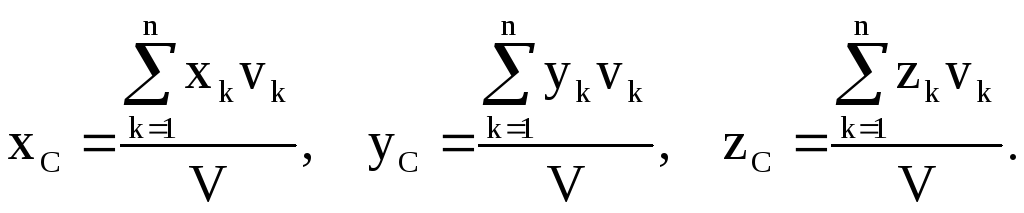(1.8.8)

Егер денені біртекті материалдық жазық дене деп алсақ, ауданның ауырлық центрінің координаталары мынандай болады:

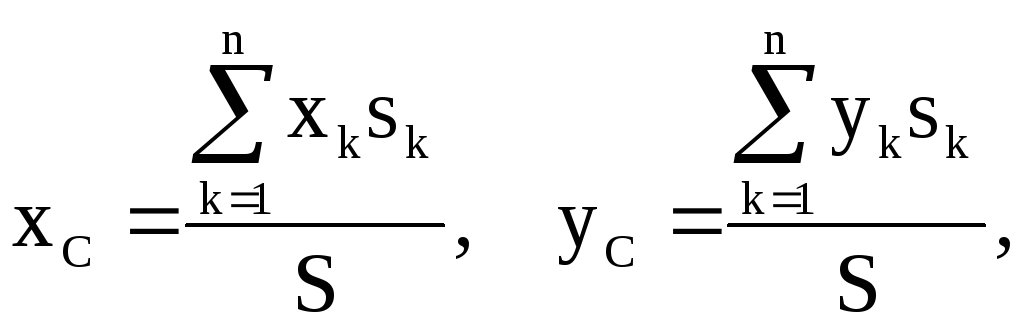(1.8.9)

мұндағы - жазық дене бөлшектерінің ауданы, - олардың ауырлық центрлерінің координаталары,- бүкіл жазық дененің ауданы.

Материялық сызықтың ауырлық центрінің координаталары мына өрнектермен анықталады:

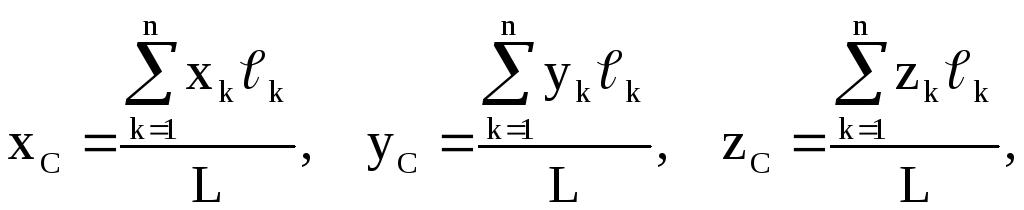(1.8.10)

мұндағы L - бүкіл сызықтың ұзындығы, - оның бөлшектерінің ұзындығы.

Сонымен, біртекті дененің ауырлық центрі сәйкес көлемнің, ауданның немесе сызықтың ауырлық центрі сияқты анықталады.