Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле

В данном разделе рассмотрим оценки определенных интегралов, а также формулу Ньютона-Лейбница позволяющую вычислять определенный интеграл.

Теорема 1 (об оценке определенного интеграла). Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т.е.

m(b-a)<<M(b-a), a<b,

где m и M- соответственно наименьшее и набольшее значения функции f(x) в интервале a;b.

Теорема 2. Если в каждой точке x интервала a;b

(x)f(x)(x),

то

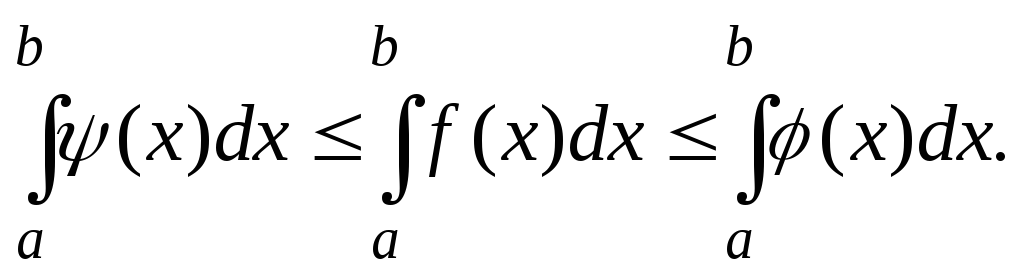
Теорема 3 (о среднем). Внутри интервала интегрирования a;b существует хотя бы одно значение x=,, для которого

.

Формула Ньютона – Лейбница.

Теорема 4. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла:

, где F(x)=f(x) (2)

Равенство (2) называется формулой Ньютона – Лейбница.

Пример. =.

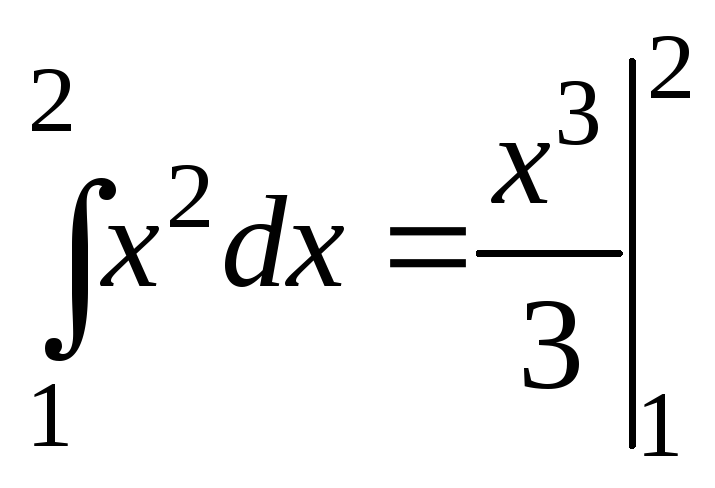Интегрирование по частям и замена переменной в определенном интеграле

1. Формула интегрирования по частям:

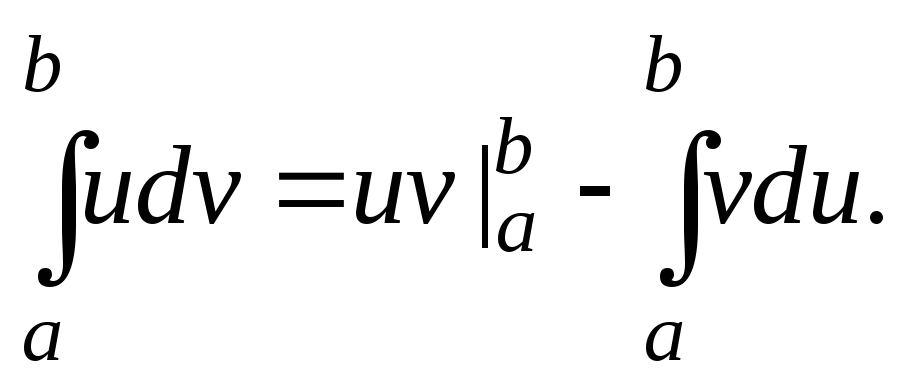
1. Формула замены переменной (подстановки):

Пусть x=(u), тогда справедлива формула

Если в интервале u₁, u₂ функции x=(u), (u) и (u) непрерывны и (u₁)=x₁, (u₂)=x₂, то

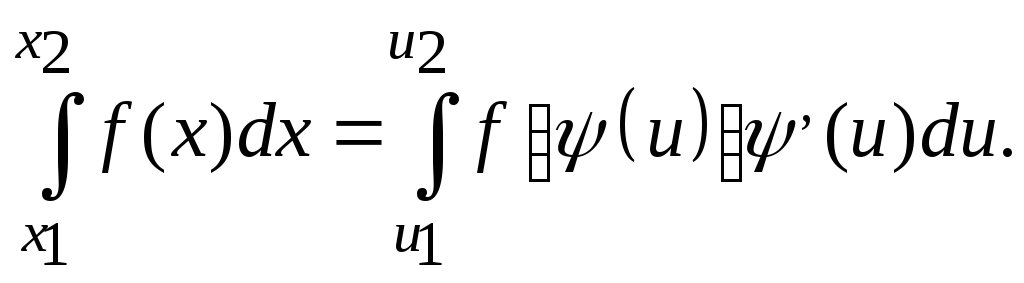
Определение. Если существует конечный предел интегральной суммы при, не зависящей от способа разбиенияотрезкана частичные отрезки и выбора промежуточных точек, то этот предел называют определённым интегралом (или интегралом Римана) от функцииf(x) на отрезке и обозначают

.

Если , то геометрически определённый интеграл выражает площадь фигуры, ограниченной графиком функцииосьюOx и двумя прямыми x=a, x=b. Эта фигура называется криволинейной трапецией.

Суммы Дарбу

Пусть на задана ограниченная функция и пусть- произвольное разбиение.,

По определению числа

,

называются соответственно нижней и верхней интегральными суммами Дарбу f, соответствующими разбиению R. Это вполне определенные числа, зависящие от f и R.

Очевидно, что

Число называетсяверхним интегралом функции на . тогда существует точная верхняя грань

называемая нижним интегралом функции на.

Теоремы о существовании интеграла от непрерывной и монотонной функции на

Т е о р е м а 1. Если функция непрерывна на, то она интегрируема на.

Т е о р е м а 2. Функция, определенная на отрезке и монотонная на нем, интегрируема на нем.

Неравенства и теорема о среднем

Т е о р е м а 1. Если f и φ интегрируемы и удовлетворяют неравенству f(x)≤ φ(x) на , то

Т е о р е м а 2. Если f интегрируема на , то

где

Т е о р е м а 3 (о с р е д н е м). Если f и φ интегрируемы на иφ(x)≥0, то

где

С л е д с т в и е. Если в этой теореме f непрерывна на , то найдутся точкитакие, чтоf(x₂)=М, f(x₁)=m и точка такая, чтопоэтому в случае непрерывной нафункцииf равенство (3) можно записать в виде

(a≤ ≤b).

Вторая теорема о среднем

Т е о р е м а. Если функция φ – неотрицательная неубывающая на отрезке , аf – интегрируемая на , то существует точкатакая, что

Основные свойства определённого интеграла:

1) ;

2) ;

3) ;

4) ;

5) Если .

6)Если .

7) Если - какая-либо первообразная функцииf(x), то справедливо равенство:

которое называется формулой Ньютона-Лейбница.