
- •Элементы логики. Функции. Действительные числа.
- •Числовые множества
- •Эквивалентные множества. Конечные и бесконечные множества
- •Бином Ньютона
- •Предел последовательности. Подпоследовательности и частичные пределы
- •Свойства последовательностей имеющих предел (сходящиеся последовательности)
- •Предел функции. Частичный предел функции
- •Непрерывные функции.
- •Производная. Основные теоремы дифференциального исчисления функций одной переменной. Формула Тейлора и её применения.
- •Исследование функций одной переменной с помощью аппарата дифференциального исчисления
- •Неопределённый интеграл
- •Интегрирование рациональных функций
- •Интегрирование иррациональных и трансцендентных функций
- •Интеграл Римана
- •Проведя в точках деления a,b прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки 1,2,…,т, так что
- •Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле
- •Приложения определенного интеграла
- •Метод прямоугольников. Пусть требуется вычислить интеграл
- •Несобственные интегралы
Интегрирование иррациональных и трансцендентных функций
Предварительно введем понятие рациональной функции от двух переменных u и v, то есть функции получающейся из этих переменных и некоторых постоянных, над которыми производятся только операции сложения, вычитания, умножения и деления R(u, v). Такова, например, функция
![]()
Если
переменные u
и v,
в свою очередь являются функциями
переменной x:
![]() то функция
то функция
![]() называется рациональной функцией от
называется рациональной функцией от
![]() и
и
![]()
Рассмотрим теперь интегралы от некоторых простейших иррациональных и трансцендентных функций сводящихся к интегралам от рациональных функций.
Интегралы вида
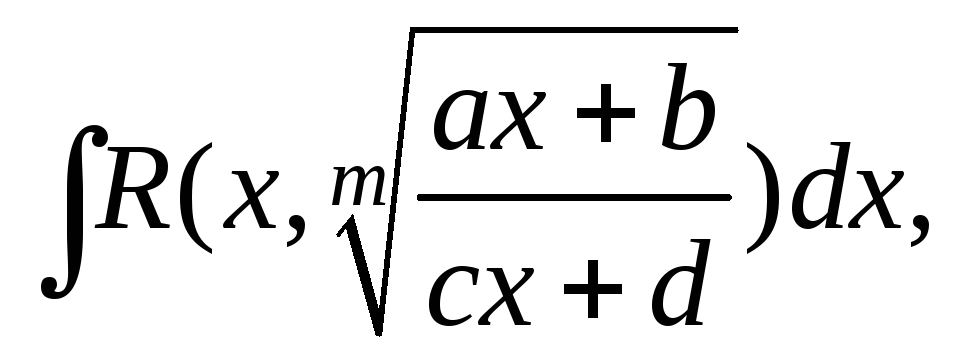 гдеa,
b,
c,
d
– некоторые
числа
гдеa,
b,
c,
d
– некоторые
числа
 m
– натуральное число. Интегралы данного
вида рационализируются подстановкой
m
– натуральное число. Интегралы данного
вида рационализируются подстановкой
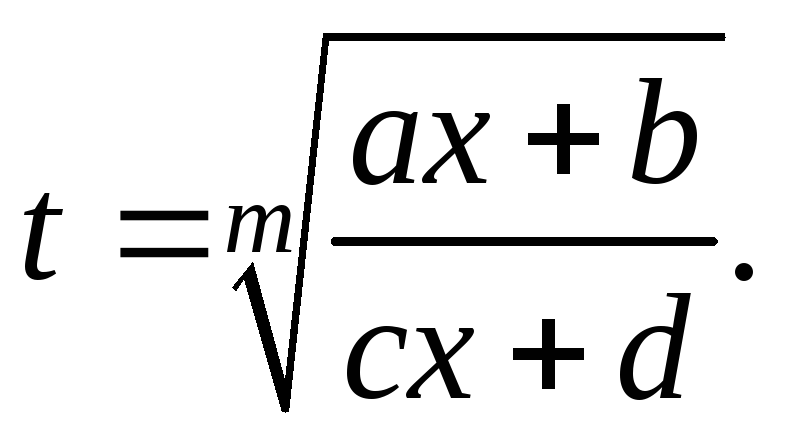
Интеграл вида
 гдеa,
b,
c
– некоторые
числа
гдеa,
b,
c
– некоторые
числа
 Данный интеграл зависит от корней
квадратного трехчлена
Данный интеграл зависит от корней
квадратного трехчлена Если этот трехчлен имеет два различных
действительных корняx1
и x2,
то он сводится к интегралу вида 1, а
именно к интегралу
Если этот трехчлен имеет два различных
действительных корняx1
и x2,
то он сводится к интегралу вида 1, а
именно к интегралу

Если x1=x2, то интеграл сводится к интегралу от рациональной функции, а именно к интегралу
![]()
Если же квадратный трехчлен не имеет вещественных корней, то с помощью подстановки Эйлера
![]()
данный интеграл приводится к интегралу от рациональной функции

Интеграл вида
 рационализируется
подстановкой
рационализируется
подстановкой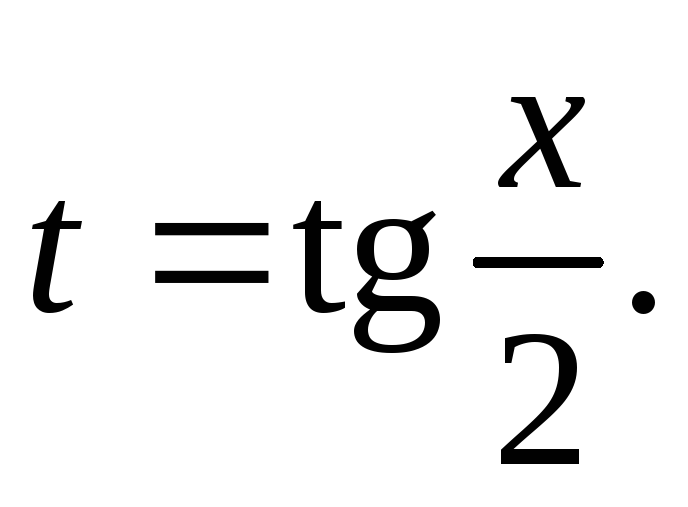 Действительно,
Действительно,
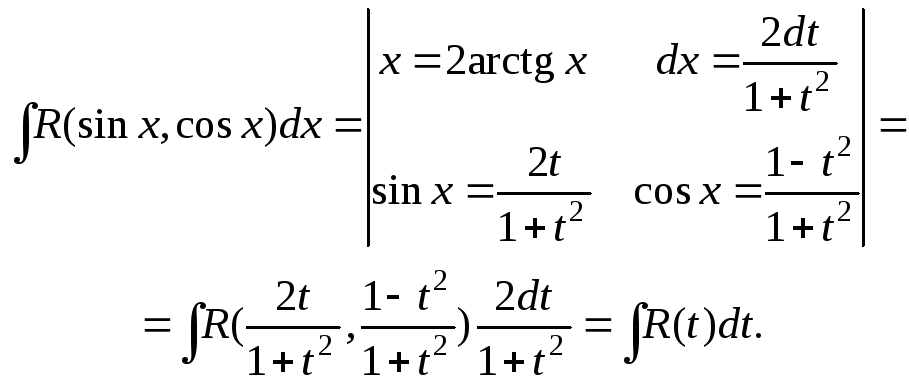
Интеграл вида
 рационализируется подстановкой
рационализируется подстановкой Действительно,
Действительно,
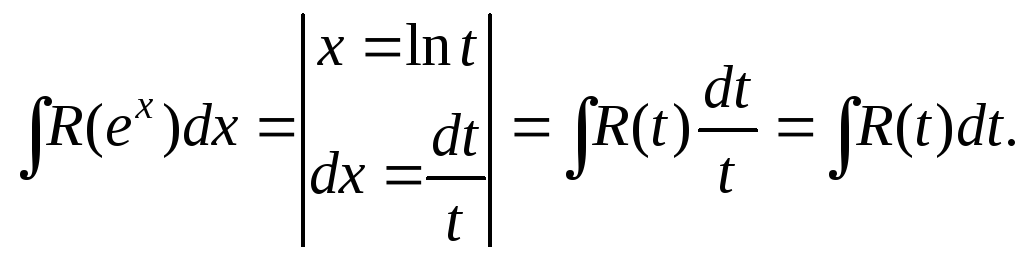
Интеграл Римана
Задача о поиске площади криволинейной трапеции приводит к понятию определенного интеграла. Криволинейная трапеция ограничена осью Ох, непрерывной функцией y=f(x), прямыми x=a и x=b, т.е. трапеция расположена над осью Ох. Разделим основание трапеции интервал a,b на n частичных интервалов x0,x1,x1,x2,…,xn-1,xn, где a=x0x1x2…xn-1xn=b.
Проведя в точках деления a,b прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки 1,2,…,т, так что
x01x1, x12x2, …, xn-1nxn.
Рассмотрим значения 1,2,…,n) и т.д.
В результате, сложив площади всех частичных трапеций, получим площадь криволинейной трапеции
S=![]() Sn=
Sn=![]()
![]() ixi,
где
xi=xi-xi-1.
ixi,
где
xi=xi-xi-1.
![]() ixi
называется n-й
интегральной суммой.
ixi
называется n-й
интегральной суммой.
![]()
![]() ixi=
ixi=![]() xdx
называется
определенным интегралом, a-нижний
предел интегрирования, b-
верхний предел интегрирования.
xdx
называется
определенным интегралом, a-нижний
предел интегрирования, b-
верхний предел интегрирования.
Определенным интегралом называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала.
Теорема
существования
определенного интеграла.
Если функция
(x)
непрерывна в замкнутом интервале a,b,
то ее n-я
интегральная сумма стремится к пределу
при стремлении к нулю длины наибольшего
частичного интервала. Этот предел, т.е.
определенный интеграл
![]() xdx,
не зависит от способа разбиения интервала
интегрирования на частичные интервалы
и от выбора в них промежуточных точек.
xdx,
не зависит от способа разбиения интервала
интегрирования на частичные интервалы
и от выбора в них промежуточных точек.
Свойства определенного интеграла.
Теорема 1 (об интеграле суммы). Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций:
![]() ,
,
где u,v,…,w – функции независимой переменной x.
Теорема 2 (о вынесении постоянного множителя). Постоянный множитель подынтегральной функции можно вынести за символ интеграла:
![]() ,
,
где u – функция аргумента x, с – константа.
Теорема 3 (о перестановке пределов). Если верхний и нижний пределы интеграла поменять местами, то интеграл изменит только знак:
![]() .
.
Если
a=b,
то![]() ,
так как
,
так как![]() .
.
Теорема 4 (о разбиении интервала интегрирования). Если интервал интегрирования a,b разбит на две части a,c и c,b, то
![]() .
.
