
- •Элементы логики. Функции. Действительные числа.
- •Числовые множества
- •Эквивалентные множества. Конечные и бесконечные множества
- •Бином Ньютона
- •Предел последовательности. Подпоследовательности и частичные пределы
- •Свойства последовательностей имеющих предел (сходящиеся последовательности)
- •Предел функции. Частичный предел функции
- •Непрерывные функции.
- •Производная. Основные теоремы дифференциального исчисления функций одной переменной. Формула Тейлора и её применения.
- •Исследование функций одной переменной с помощью аппарата дифференциального исчисления
- •Неопределённый интеграл
- •Интегрирование рациональных функций
- •Интегрирование иррациональных и трансцендентных функций
- •Интеграл Римана
- •Проведя в точках деления a,b прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки 1,2,…,т, так что
- •Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле
- •Приложения определенного интеграла
- •Метод прямоугольников. Пусть требуется вычислить интеграл
- •Несобственные интегралы
Неопределённый интеграл
Пусть
на интервале
![]() задана функция
задана функция![]() .
Если
.
Если![]() ,
где
,
где![]() ,
то функция
,
то функция![]() называется первообразной функцией
функции
называется первообразной функцией
функции![]() на интервале
на интервале![]() .
Совокупность первообразных
.
Совокупность первообразных![]() ,
гдеC
– произвольная постоянная, функции
,
гдеC
– произвольная постоянная, функции
![]() ,
где
,
где![]() ,
называется неопределённым интегралом
функции
,
называется неопределённым интегралом
функции![]() :
:
![]() .
.
Основные правила интегрирования:
1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
4)
Если
![]() ,
то
,
то![]() при условии, чтоa,b
– постоянные числа,
при условии, чтоa,b
– постоянные числа,
![]() .
.
Основные методы интегрирования.
Непосредственное интегрирование. Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием.
Пример.
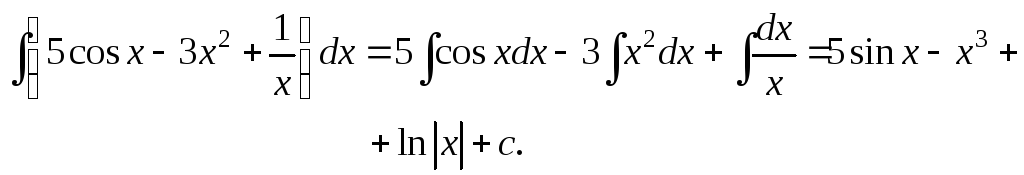
Метод подстановки. Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, то есть перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной. Он основан на следующей теореме.
Теорема 1. Пусть функция x=j(t) определена и дифференцируема на некотором промежутке Т и пусть Х µ множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
![]()
Эта формула называется формулой замены переменных в неопределенном интеграле.
Пример.
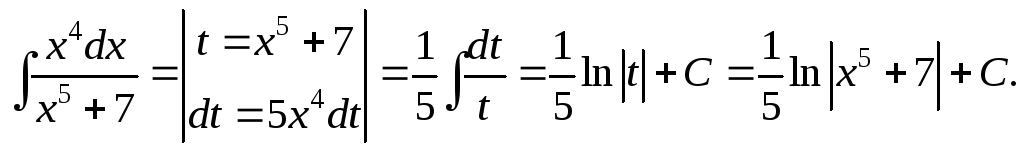
Интегрирование по частям. Метод интегрирования по частям основан на применении формулы дифференцирования произведения двух функций.
Теорема 2. Пусть функции u(x) и v(x) определены и дифференцируемы на некотором промежутке Х и пусть функция u’(x)v(x) имеет первообразную на этом промежутке. Тогда на промежутке Х функция u(x)v’(x) также имеет первообразную и справедлива формула
![]()
Эта формула называется формулой интегрирования по частям в неопределенном интеграле. В качестве функции u(x) принимается функция которая дифференцированием упрощается или трансцендентные функции ln x, arctg x, arcsin x.
Пример 1.

Пример 2.
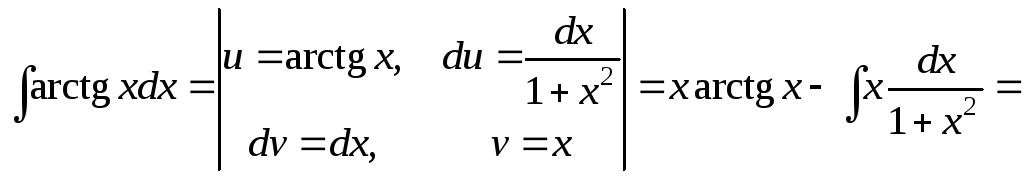
![]()
Таблица простейших интегралов
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() ,
,
![]() ,
,
![]() .
8.
.
8.
![]() .
.
9.
![]() 10.
10.
![]() .
.
11.
![]() 12.
12.
![]()
13.
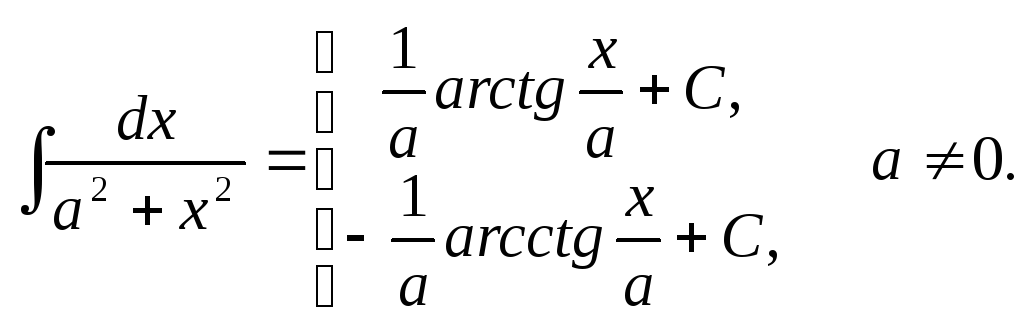
![]() .
.
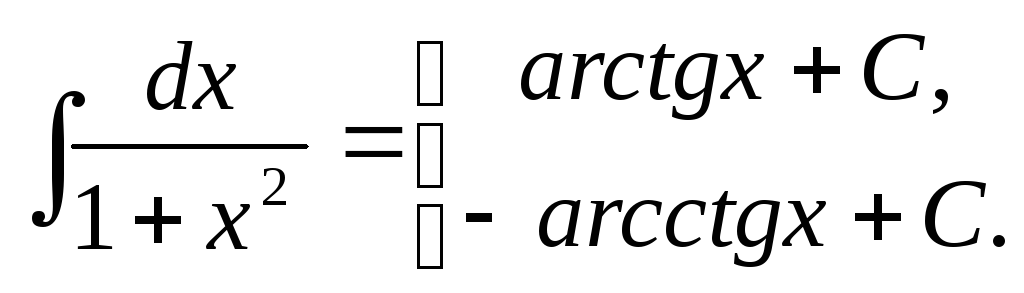
14.
![]() =
=![]() ,
,
![]() .
.
15.
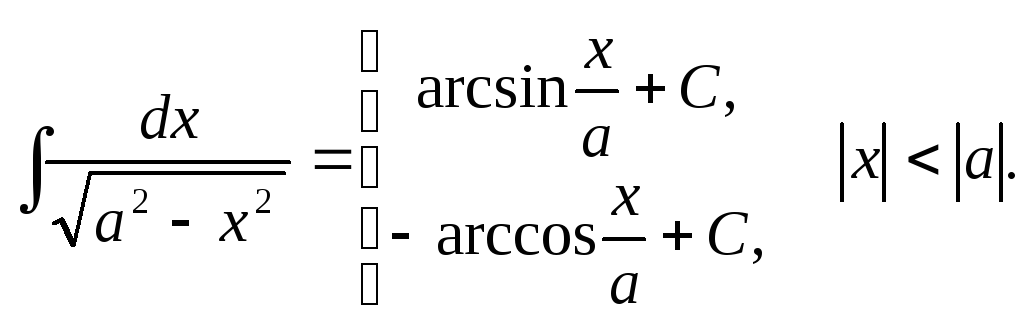
![]() .
.
![]()
![]() =
=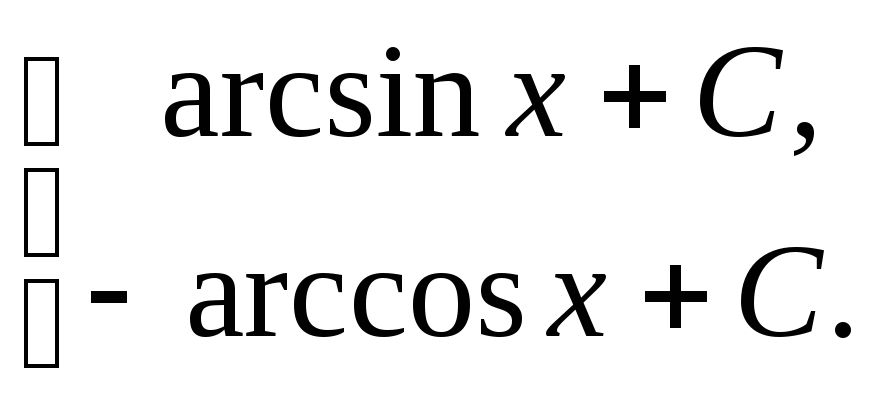
![]() .
.
16.
![]() =
=![]() .
.
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
Интегрирование рациональных функций
Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют рациональные функции, то есть функции, которые можно представить в виде дроби
![]()
где P(x), Q(x) – многочлены.
Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то, выполнив деление, получим
![]()
где W(x) – некоторый многочлен, а R(x) – многочлен степени ниже, чем Q(x).
Пример.
![]()
Многочлен W(x) представляет собой линейную комбинацию целых неотрицательных степеней x и поэтому может быть проинтегрирован. Теперь рассмотрим вопрос интегрирования правильной дроби из последнего соотношения.
Знаменатель
правильной дроби разлагается на множители
вида
![]() и
и![]() а дробь разлагается на сумму элементарных
дробей следующим образом
а дробь разлагается на сумму элементарных
дробей следующим образом
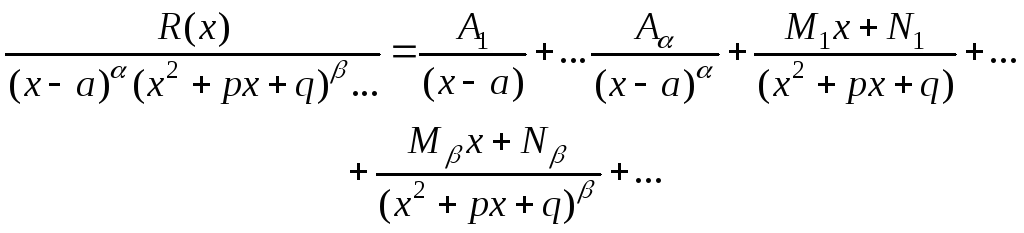
Интегралы данных дробей приводятся к интегралам следующего вида
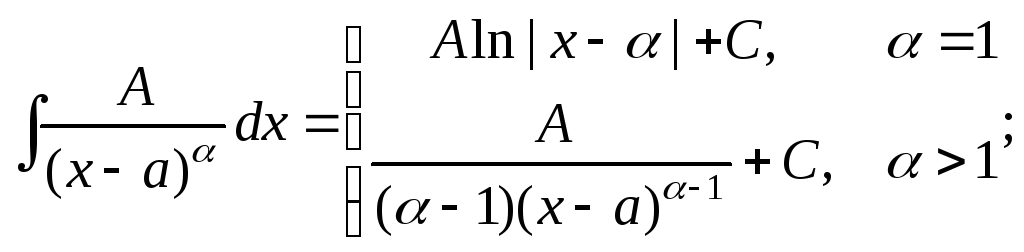
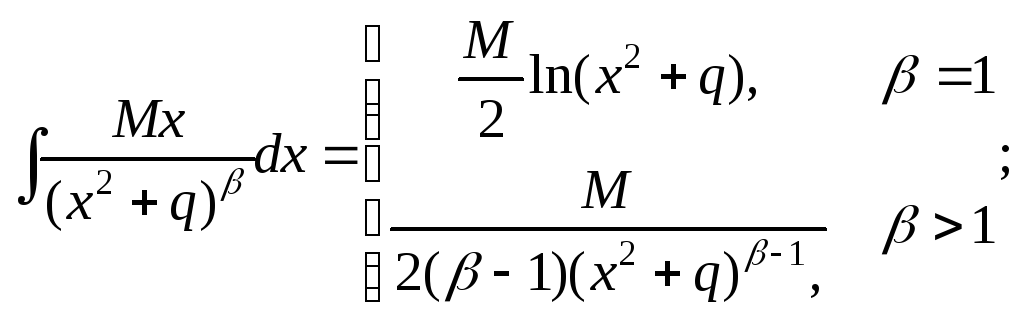
![]()
Интеграл
![]() вычисляется по рекуррентной формуле
вычисляется по рекуррентной формуле
![]()
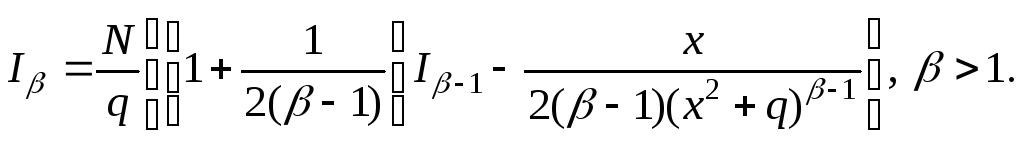
Таким образом, можно сделать вывод о том, что всякая рациональная функция может быть проинтегрирована в элементарных функциях.
