
- •Элементы логики. Функции. Действительные числа.
- •Числовые множества
- •Эквивалентные множества. Конечные и бесконечные множества
- •Бином Ньютона
- •Предел последовательности. Подпоследовательности и частичные пределы
- •Свойства последовательностей имеющих предел (сходящиеся последовательности)
- •Предел функции. Частичный предел функции
- •Непрерывные функции.
- •Производная. Основные теоремы дифференциального исчисления функций одной переменной. Формула Тейлора и её применения.
- •Исследование функций одной переменной с помощью аппарата дифференциального исчисления
- •Неопределённый интеграл
- •Интегрирование рациональных функций
- •Интегрирование иррациональных и трансцендентных функций
- •Интеграл Римана
- •Проведя в точках деления a,b прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки 1,2,…,т, так что
- •Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле
- •Приложения определенного интеграла
- •Метод прямоугольников. Пусть требуется вычислить интеграл
- •Несобственные интегралы
Предел функции. Частичный предел функции
Предельная точка множества. Предел функции в точке.
Определение
1.
Пусть
![]() .
Число
.
Число
![]() называется
предельной точкой множества
X,
если
называется
предельной точкой множества
X,
если
![]() .
.
Из
определения следует, что любая окрестность
точки
![]() содержит
точку из множества X,
отличную
от
содержит
точку из множества X,
отличную
от
![]() .
Сама
точка
.
Сама
точка
![]() может принадлежать, а может и не
принадлежать множеству
X.
может принадлежать, а может и не
принадлежать множеству
X.
Определение
2.
Значение
![]() есть
предельная точка множества X,
если
есть
предельная точка множества X,
если
![]() .
.
Значение
![]() есть
предельная точка множества X,
если
есть
предельная точка множества X,
если
![]() .
.
Определение
3.
Точка
![]() ,
не являющаяся предельной точкой множестваX,
называется
изолированной точкой множества X,
т. е.
,
не являющаяся предельной точкой множестваX,
называется
изолированной точкой множества X,
т. е.
![]() .
.
Определение
4.
Число
![]() называется
предельной точкой множества
называется
предельной точкой множества
![]() ,
если
из этого множества можно выделить
последовательность (xn)
различных точек, сходящуюся
к
,
если
из этого множества можно выделить
последовательность (xn)
различных точек, сходящуюся
к
![]() .
.
Определения 1 и 4 эквивалентны.
Пусть
![]() и
и
![]() -
предельная
точка множества X.
-
предельная
точка множества X.
Определение
5
(Гейне).
Функция
f
имеет предельное значение при
![]() (или
в точке
(или
в точке
![]() ),
если существует такое число
),
если существует такое число
![]() ,
что для произвольной последовательности
(хn)
значений
,
что для произвольной последовательности
(хn)
значений
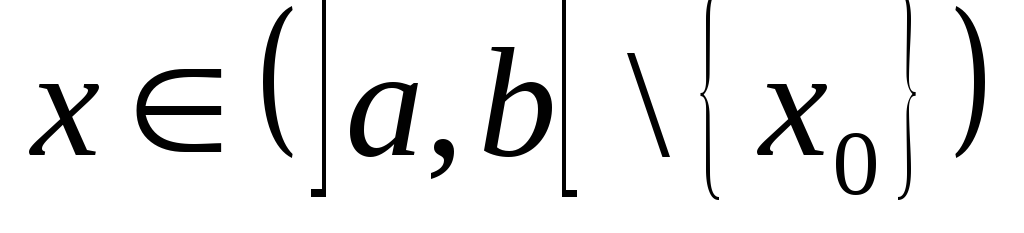 ,сходящейся
к точке
,сходящейся
к точке
![]() ,
соответствующая последовательность
значений функции (f(xn))
сходится к точке А.
,
соответствующая последовательность
значений функции (f(xn))
сходится к точке А.
Определение
6
(Коши).
Функция
f
имеет
предел при
![]() ,
если
,
если
![]() .
.
При этом число А называем пределом (или предельным значением) функции f в точке х0 и записываем
![]() или
или
![]() .
.
Определения Гейне и Коши эквивалентны.
Введем понятие одностороннего предела.
Определение
7
(Гейне). Функция
f
имеет в точке,
![]() предел слева (справа), если существует
такое число
предел слева (справа), если существует
такое число
![]() ,
что для
произвольной последовательности (хn)
значений
х,
,
что для
произвольной последовательности (хn)
значений
х,
![]()
![]() ,
сходящейся к точке
,
сходящейся к точке
![]() при
при
![]() ,
соответствующая
последовательность
(f(xn))
значений функции f
сходится к точке А.
,
соответствующая
последовательность
(f(xn))
значений функции f
сходится к точке А.
Определение 8 (Коши). Функция f имеет в точке х0 предел слева (справа), если
![]() .
.
Число
А
называем
пределом
слева (справа) функции
f
в точке
![]() и
обозначаем
и
обозначаем
![]() или
или
![]()
Функция f имеет предел в точке х0 тогда и только тогда, когда в этой точке существуют и равны между собой пределы слева и справа.
Теорема
(критерий
Коши). Функция
f
имеет конечный предел
в точке
![]() тогда
и только
тогда, когда
тогда
и только
тогда, когда
![]() .
.
Особую роль играют два замечательных предела:
![]()
Если
![]() ,
то
,
то
![]() .
.
![]()
Ограниченность функции.
Функция
![]() ,
,
![]() называется ограниченной намножестве
X,
если
существуют числа
m
и M
такие,
что
называется ограниченной намножестве
X,
если
существуют числа
m
и M
такие,
что
![]() .
.
Непрерывные функции.
Определение
1. Функция
![]() ,
,![]() ,
называется непрерывной вточке
,
называется непрерывной вточке
![]() ,
если выполняется
одно из эквивалентных условий:
,
если выполняется
одно из эквивалентных условий:
1)
![]() (1)
(1)
2)
для произвольной последовательности
(хn)
значений
![]() ,
сходящейсяпри
,
сходящейсяпри
![]() к точке
к точке![]() ,
соответствующая последовательность
,
соответствующая последовательность![]() значений функции сходится при
значений функции сходится при![]() к
к![]() ;
;
3)
![]() или
или![]() при
при![]() ;
;
Из
определения непрерывности функции f
в точке
![]() следует,
что
следует,
что
![]() .
.
Определение
2. Если
функция f
непрерывна
в каждой точке
интервала
![]() ,
то
функция
,
то
функция
![]() называется
непрерывной на этом интервале.
называется
непрерывной на этом интервале.
Определение
3. Функция
![]() называется
непрерывной в
точке
называется
непрерывной в
точке
![]() слева (справа), если выполняется одно
из эквивалентных условий:
слева (справа), если выполняется одно
из эквивалентных условий:
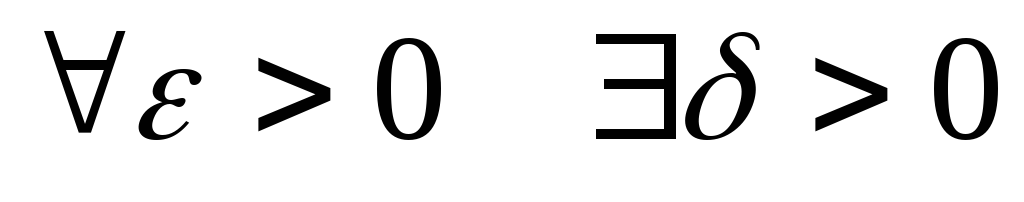 такое,
что неравенство (1)
выполняется,
как только
такое,
что неравенство (1)
выполняется,
как только
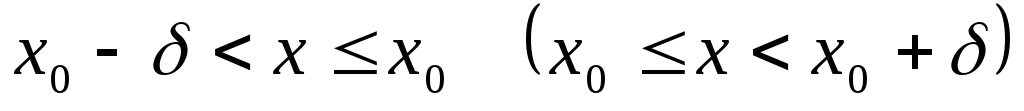 ;
;для произвольной последовательности (хn) значений
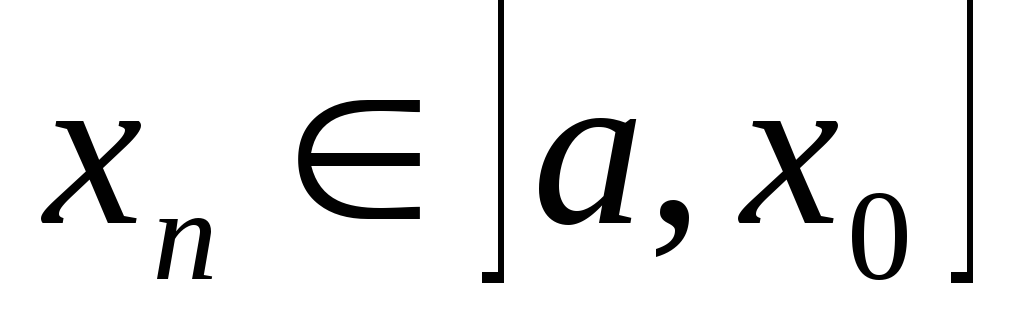 ,
, сходящейсяпри
сходящейсяпри
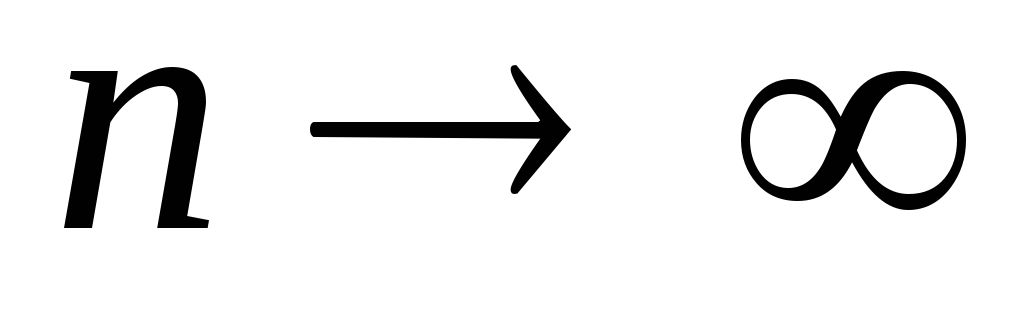 к точке
к точке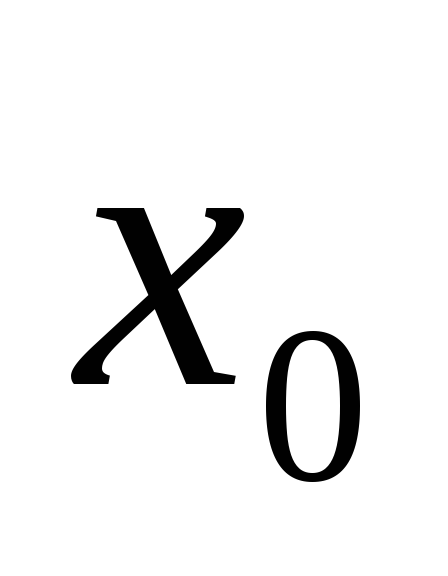 ,
соответствующая последовательность
,
соответствующая последовательность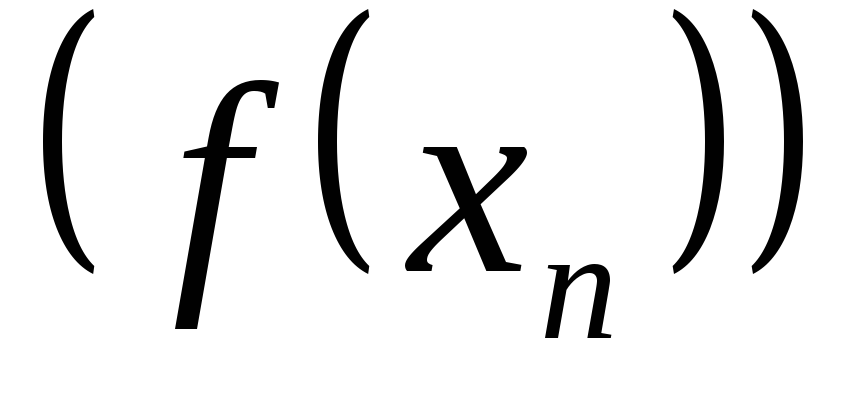 значений функцииf
сходится к
значений функцииf
сходится к
 .
.
Функция
![]() непрерывна во внутренней точке
непрерывна во внутренней точке![]() тогдаи
только тогда,
когда
она в этой точке непрерывна слева и
справа.
тогдаи
только тогда,
когда
она в этой точке непрерывна слева и
справа.
Теорема
1.
Если функция
![]() ,
непрерывна
в
точке
,
непрерывна
в
точке
![]() ,
афункция
,
афункция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
где
,
где![]() ,
токомпозиция
,
токомпозиция
![]() непрерывна
в точке t0.
непрерывна
в точке t0.
Теорема
2.
Пусть функции
![]() и
и![]() ,
,![]() ,
непрерывны
в точке
,
непрерывны
в точке
![]() .
Тогда функции
.
Тогда функции
![]()
непрерывны
в точке
![]() .
.
Все элементарные функции непрерывны в области существования.
Точки разрыва функции и их классификация. Особые точки функции.
Определение.
Если функция
![]() не является непрерывной в точке
не является непрерывной в точке![]() ,
то говорят, что она терпит разрыв в этой
точке. При этом точка
,
то говорят, что она терпит разрыв в этой
точке. При этом точка![]() называется точкой разрыва функции
называется точкой разрыва функции![]() .
.
Точки
разрыва функции
![]() классифицируем следующим образом:
классифицируем следующим образом:
1.
Пусть
![]() - точка разрыва функции
- точка разрыва функции![]() и существует
и существует![]() ,
конечный или бесконечный. При этом:
,
конечный или бесконечный. При этом:
а)
если
![]() конечный, то
конечный, то![]() называем точкой устранимого разрыва
функции
называем точкой устранимого разрыва
функции![]() ;
;
б)
если
![]() ,
то
,
то![]() называем точкой разрыва типа полюса.
называем точкой разрыва типа полюса.
2.
Если
![]() не существует, то точку
не существует, то точку![]() называем точкой существенного разрыва
функции
называем точкой существенного разрыва
функции![]() .
При этом:
.
При этом:
а)
если существуют конечные пределы
![]()
![]() ,
то точку
,
то точку![]() называем точкой разрыва первого рода
функции
называем точкой разрыва первого рода
функции![]() ;
;
б) все остальные точки существенного разрыва называем точками разрыва второго рода функции f.
Равномерная непрерывность.
Определение.
Функция
![]() называется равномерно-непрерывной на
множествеX,
если
называется равномерно-непрерывной на
множествеX,
если
![]() .
.
Если функция f не является равномерно-непрерывной, то это означает следующее:
![]() .
.
Теорема
Кантора.
Если функция
![]() непрерывна на сегменте
непрерывна на сегменте![]() ,
то она равномерно непрерывна на этом
сегменте.
,
то она равномерно непрерывна на этом
сегменте.
