Метод прямоугольников. Пусть требуется вычислить интеграл

I=

где f(x) –непрерывная функция. Для простаты рассуждений ограничимся случаем, когда f(x) . В основе приближенного вычисления определенного интеграла I лежит его геометрический смысл: выражает площадь криволинейной трапеции. Разобьем отрезок [a,b] на n равных частичных отрезков точками k= Длину каждого отрезка назовемшагом разбиения.

На каждом частичном отрезке [x_k: x_{k- 1}] выберем точку и вычислимf( Тогда по определению 9.1

Следовательно,

(9.15)

Формула (9.15) называется формулой прямоугольников.

Предположим, что существует непрерывная вторая производная (9.16)

где

Метод трапеций. Сумма площадей «прямолинейных» трапеций приближенно равна площади криволинейной трапеции aАВb, т.е.

где

- основания «прямолинейных» трапеций: -их высоты. Таким образом, получена приближенная формула

(9.17) которая называется формулой трапеций.

Метод параболических трапеций (метод Симпсона).

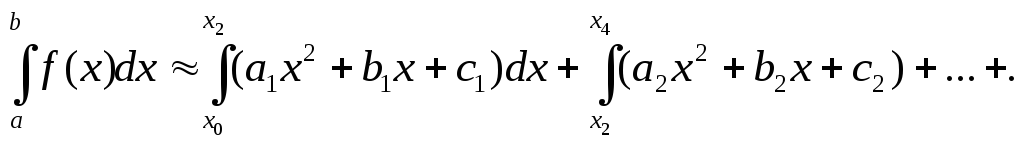
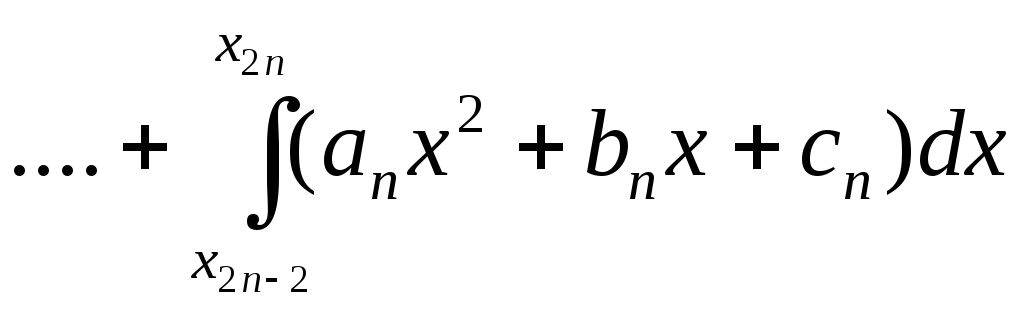
Просуммировав эти интегралы, получим:

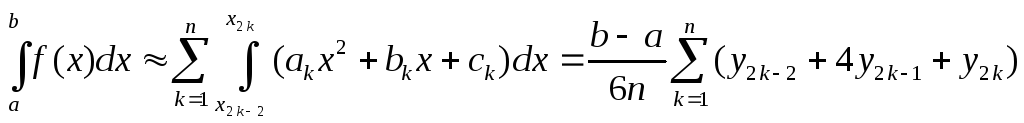или

Эта формула называется формулой парабол или формулой Симпсона.

Несобственные интегралы

Понятие несобственных интегралов.

При введении понятия определенного интеграла как предела интегральной суммы предполагалось, что выполняются следующие условия: 1) пределы интегрирования a и b являются конечными; 2) подынтегральная функция f(x) на отрезке непрерывна или имеет конечное число точек разрыва первого рода. В этом случае определенные интегралы называютсясобственными. Если хотя бы одно из указанных условий не выполняются, то интегралы называются несобственными

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f(x) на промежутке называется предел I(b) при b

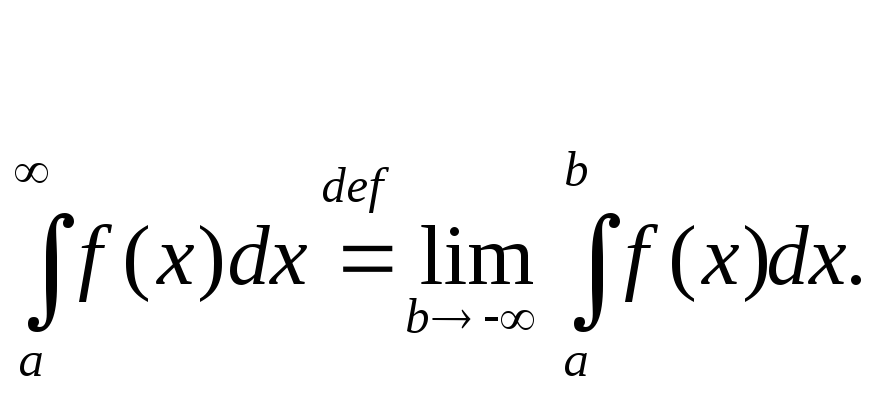
Аналогично определяется несобственный интеграл с бесконечным верхним пределом интегрирования от непрерывной функции f(x) на промежутке

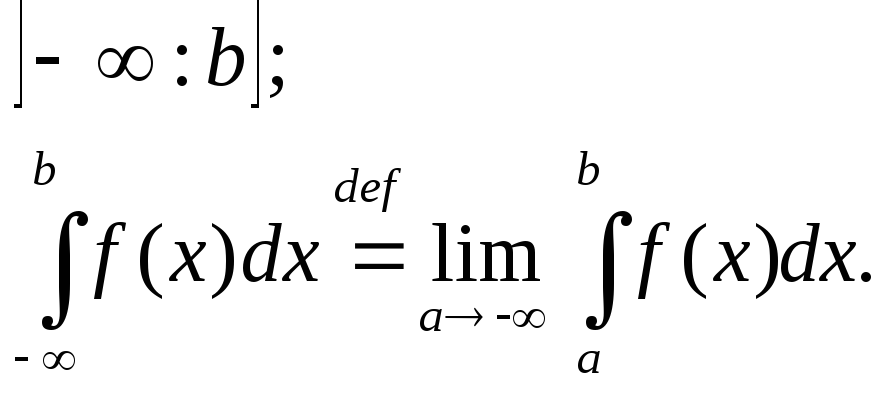
Если пределы в правых частях этих формул (существуют и конечны, то соответствующие несобственные интегралы называются сходящимися, если пределы не существуют или бесконечны, -то расходящимся.

Несобственный интеграл с двумя бесконечными пределами интегрирования от непрерывной функции f(x) на промежутке обозначаемый

, предварительно представляют в виде

Тогда по определению

причём этот несобственный интеграл называется сходящимся, если оба предела существуют. Если хотя бы один из пределов не существует или бесконечен, то несобственный интеграл называется расходящимся.

Теорема 1. (признак сравнения).

Если на промежуткеопределены две неотрицательные функцииf(x) и интегрируемые на каждом конечном отрезкепричем,то из сходимости интеграласледует сходимость интеграла, а из расходимости интеграласледует расходимость интеграла

.

Теорема 2. (предельный признак сравнения).

Если на промежутке определены две положительные функцииf(x) и интегрируемые на любом конечном отрезкеи существует конечный предел

то несобственные интегралы исходятся или расходятся одновременно.

Теорема 3.Если на промежутке функцияy=f(x) меняет знак несобственный интеграл сходится, то сходится также и.Отметим, что несобственный интегралназывают абсолютно сходящимся, если сходится интеграл

Определение. Несобственным интегралом от функции f(x) , непрерывной на промежутке [a;b] и имеющей бесконечный разрыв в точке x=b, или несобственным интегралом второго рода называется предел интеграла при:

.

Аналогично если функция f(x) имеет бесконечный разрыв в точке х=а, то полагают

Если же функция f(x) имеет разрыв второго рода в некоторой внутренней точке с отрезка [a;b], то пользуясь свойством аддитивности определенного интеграла , данный интеграл представляют в виде суммы двух интегралов:

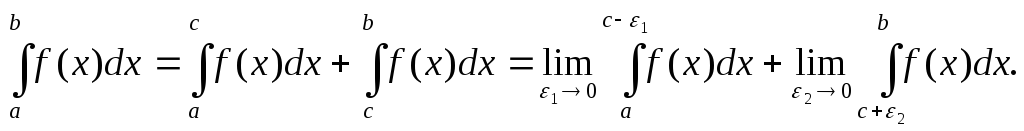
Теорема 4. (признак сравнения)

Пусть в левой окрестности точки b (точки a) определены две неотрицательные функции f(x) и , причем . Тогда из сходимости несобственного интеграла следует сходимость интеграла , а из расходимости несобственного интеграла следует расходимость интеграла .

Теорема 5.(предельный признак сравнения).

Пусть функции f(x) и φ(x) положительны на промежутке [a; b], b- точка бесконечного разрыва функций f(x) и φ(x) . Тогда если существует конечный предел , то несобственные интегралыисходятся или расходятся одновременно.

Несобственные интегралы с особенностями в нескольких точках

Пусть (a, b) есть интервал, конечный или бесконечный, и на нем задана функция f такая, что интервал

(1)

имеет особенности только в точках a, b. Это значит, что a = - ∞ или, если a – конечная точка, то в ее окрестности функция f неограниченна; также b =+∞ или, если b – конечная точка, то в окрестности ее f неограниченна. Кроме того, функция f интегрируема на любом отрезке [a’, b’], где a<a’<b’<b.

Произвольная точка с интервала (a, b) делит его на два частичных интервала (a, с) (с, b).

Интеграл

(2)

имеет единственную особенность (в точке а); интеграл

(3)

также имеет единственную особенность (в точке b). Для интервалов (2) и (3) мы уже знаем, в каком случае они существуют (сходятся) как несобственные интегралы.

По определению, несобственный интеграл (1) существует (сходится) в том и только в том случае, если каждый из интегралов (2) и (3) существует. При этом полагают

Это определение не зависит от с. В самом деле, если a< с< с’<b, то

(4)

где интеграл - собственный, и, аналогично,

(5)

Сложив (4) и (5) и сократив на получим

29