Об’ємна густина енергії магнітного поля

(6.27)

де V = SL - об’єм соленоїда.

Речовина є магнетиком, тобто вона під дією магнітного поля здатна придбати магнітний момент (намагнічуватися). Речовина, що намагнічується у зовнішньому магнітному полі проти напрямку цього поля, є діамагнетиком. Однак разом з діамагнетиками існують парамагнетики - речовини, що нама­гнічуються у зовнішньому магнітному полі за напрямком поля.

Намагніченість магнетиків

, (6. 28)

де  - магнітна сприйнятливість речовини.

Кількісною мірою магнітної дії змінного електричного поля служить струм зміщення. Густиною струму зміщення називають вектор

, (6. 29)

де - вектор електричного зміщення.

Струмом зміщення крізь довільню поверхню S називається фізична величина, що дорівнює потоку вектора густини струму зміщення крізь цю поверхню:

, (6. 30)

де -потік вектора електричного зміщення крізь поверхню S.

Теорія Максвела грунтується на чотирьох рівняннях (у інтегральній формі):

1. (6. 31)

Це рівняння визначає, що джерелами електричного поля можуть бути не тільки електричні заряди, але і змінні у часі магнітні поля.

2. Узагальнена теорема про циркуляцію вектора :

(6. 32)

Це рівняння показує, що магнітні поля можуть збуджуватися або рухомими зарядами (електричними струмами), або електричними полями.

3. Теорема Гауса для поля :

. (6. 33)

4. Теорема Гауса для поля :

. (6. 34)

7. Коливання та хвилі

Коливаннями називаються рухи чи процеси, які характеризуються визначеною повторністю у часі. Фізична природа коливань може бути різною, тому розрізняють коливання механічні, електромагнітні та ін. Однак різні коливальні процеси описуються однаковими характеристиками и однаковими рівняннями.

Гармонійні коливання - коливання, при яких значення коливної величини змінюється з часом за законом синуса (косинуса). Гармонійні коливан­ня величини s описуються рівнянням типу

s = Acos(₀t + ), (7.1)

де А - максимальне значення коливної величини, що називається амплітудою коливань, ₀ - кругова (циклічна) частота,  - початкова фаза коливань у мо­мент часу t = 0, (₀t + ) - фаза коливання у момент часу t. Оскільки косинус змінюється у межах від +1 до -1, то s може приймати значення від +А до –A.

Певні стани системи, що здійснює гармонійні коливання, повторюються через проміжок часу Т - період коливання, за який фaзa кoливaння отримає пpиpіст 2.

(7. 2)

Beличинa, oбеpнена до пepіoдy кoливaнь,

 = , (7. 3)

тобто чиcлo пoвниx кoливaнь, що здійснюються у одиницю часу, нaзивaєтьcя чacтoтoю коливань. Із (7. 2) та (7. 3)

₀ = 2. (7. 4)

Одиниця частоти - герц (Гц): 1 Гц - чacтoтa періодичного пpoцecу, при якому зa 1 c здійснюється oдин цикл пpoцecу.

Математичний маятник - це ідеалізована cиcтeмa, яка cкладається з мaтeріальноі точки масою т, підвішеної на невагомій нерозтягнутій нитці. Точка коливається під дією сили тяжіння.

Період малих коливань математичного маятника

, (7. 5)

де l – довжина маятника, g – прискорення вільного падіння.

Пружинний маятник - це вантаж масою т, подвішений на абсолютно пружній пружині, який здійснює гармонійні коливання під дією рпужної сили F = - kx, де k - жорсткість пружини. Рівняння руху маятника

или

Пружинний маятник здійснює гармонійні коливанняя згідно з законом х = А cos (₀t +  ) з циклічною частотою

(7. 6)

і періодом

(7. 7)

Потенціальна енергія пружинного маятника дорівнює

(7. 8)

Затухаючі коливання - коливання, амплітуда яких через втрати енергії реальною коливальною системою з часом зменьшується.

Диференційне рівняння вільних затухаючих коливань лінійної системи задається в вигляді

(7. 9)

де s - коливальна величина,  = const - коефіціент загасання, ₀ - циклічна частота вільних незатухаючих коливань тієї ж коливальної системи, тобто при  = 0 (при відсутності втрат енергії) називається власною частотою коливальної системи.

Рис. 7.1

Розв’язання рівняння (7. 9) у разі малих затухань (²  ₀²)

s = A_oe^-tcos(t+), (7.10)

де

А = А_ое^-t (7.11)

- амплітуда затухаючих коливань, А₀ - початкова амплітуда. Залежність (7.11) показана на рис. 7.1.

Проміжок часу  = 1/, за який амплітуда затухючих коливань зменшується у е раз, називається часом релаксації.

Якщо затухання є малим, тоді період затухаючих коливань дорівнює

(7.12)

Якщо A(t) и А(t+Т) - амплітуди двох послідовних коливань, які відповідають моментам часу, що відрізняється на період, тоді відношення

(7.13)

називається декрементом затухання, а його логарифм

(7.14)

- логарифмічним декрементом затухання; N_e - число коливань, що здійснюються за час зменьшення амплітуди у е раз.

Добротність Q при малих значеннях логарифмічного декремента дорівнює

(7.15)

(якщо загасання є малим ( ² << ), тоді T прийнято рівним Т₀).

Линійне неоднорідне диференційне рівняння вимушених коливань

, (7.16)

де х_о у випадку механічних коливань дорівнює F_o/m, а у випадку електромагніт­них - U_m/L.

Розв’язання цього неоднорідного рівняння має вигляд

(7.17)

Для електромагнітних коливань, враховуючи, що та, маємо

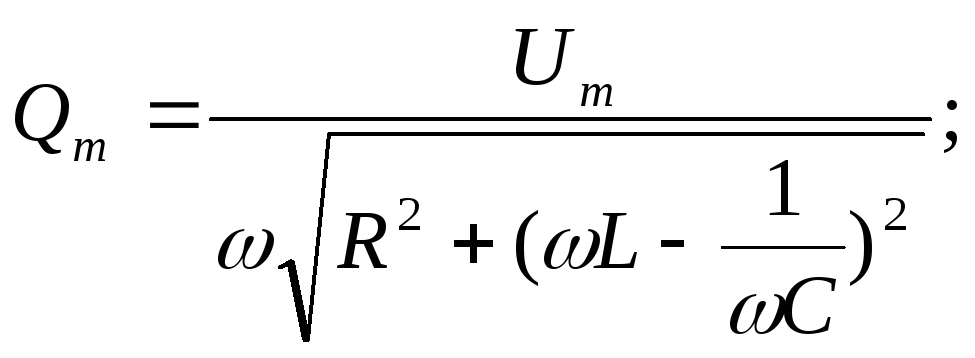
, (7.18)

звідкіля

. (7.19)

Зсув фаз між струмом та прикладеною напругою

. (7. 20)

Явище різкого зростання амплітуди вимушених коливань при наближенні частоти вимушеної сили (частоти вимушеної змінної напруги) до ча­стоти, рівної чи близької власній частоті коливальної системи, називається резонансом (відповідно механічним чи електричним).

Резонансна частота

. (7. 21)

При ²<< значення _рез практично збігається з власною частотою ₀ коливальної системи. Резонансна амплітуда

. (7. 22)

Процес поширення коливань у суцільному середовищі називається хвильовим про­цесом (або хвилею). Пружна хвиля називається гармонійною, якщо відповідні їй коливання частинок середовища є гармонійними.

Рис. 7. 2

Відстань між найближчими частинками, що коливаються у однаковій фазі, називаються довжиною хвилі l (рис. 7. 2). Довжина хвилі дорівнює відстані, на яку поширюється певна фаза коливання за період

 = vT,

або, враховуючи, що T = 1/, де  - частота коливань,

v = v.

Розглянемо додавання двох гармонійних коливань однако­вого напрямку та однакової частоти. Зміщення х коливального тіла буде сумою зміщень x₁ и х₂, які записуються таким чином:

x₁ = A₁ cos(₀t + ₁), х₂ = A₂ cos(₀t + ₂).

Репрезентуємо обидва коливання за допомогою векторів и (рис. 7. 3).

Проекція результуючого вектора на вісь х

х = х₂ + x₂.

Вектор представляє результуюче коливання. Цей вектор обертається з тією ж кутовою швидкістю ₀, як і вектори и , таким чином результуючий рух буде гармонійним коливанням з частотою ₀, амплітудою A та початковою фазою .

Рис. 7. 3

(7. 23)

(7. 24)

Нехай є два гармонійні коливання однакової час­тоти , що відбуваються у взаємно перпендикулярних напрямках вздовж осей х і у

(7. 25)

де  - різниця фаз обох коливань, А и В - амплітуди коливань, що додаються. Рівняння траєкторії результуючого коливання є рівнянням еліпса , осі якого орієнтовані відносно координат довільно:

(7. 26)

Об’ємна густина w енергії електромагнітної хвилі складається з об’ємних густин w_ел і w_м електричного та магнітного полів:

w = w_ел + w_м = ₀E²/2 + ₀ H² /2. (7. 27)

Враховуючи вираз

, (7. 28)

отримаємо, що густини енергії електричного та маг­нітного полів у кожний момент часу однакові, тобто w_ел= w_м . Тому

w = 2 w_ел = ₀E² = .(7. 29)

Помноживши густину енергії w на швидкість v розповсюдження хвилі у середовищі (), отримаємо модуль густини потоку енергії:

S = wv = EH (7. 30)

Вектор густини потоку електромагнітної енергії називається вектором Умова - Пойнтінга:

. (7. 31)

Вектор направлений у бік поширення електромагнітної хвилі.

Найпростішим випромінювачем електромагнітних хвиль є електричний диполь, електричний момент якого змінюється у часі за гармонійним законом

, (7. 32)

де - амплітуда вектора.

Інтенсивність випромінювання диполя у хвильовій зоні

, (7. 33)

де r - відстань від точки до спостерігача,  - кут між напрямком радіус - вектора та віссю диполя.