6. Електромагнетизм

Подібно до того, як у просторі, який оточує електричні заряди, виникають електростатичні заряди, так і у просторі, що оточує струм та постійні магніти, виникає силове магнітне поле. Наявність магнітного поля виявляється за силовою дією на внесені в нього провід­ники зі струмом чи постійні магніти.

Електричне поле діє як на нерухомі, так і на рухомі у ньому електричні заряди. Важлива особливість магнітного поля полягає у тому, що воно діє тільки на рухомі у цьому полі електричні заряди. Отже, щоб характеризувати магнітне поле, потрібно розглянути його дію на певний струм.

При дослідженні магнітного поля використовується замкнений плоский контур з током (рамка зі струмом). Орієнтація контура у просторі визначається напрямком нормалі до контура. Напрямок нормалі визначається правилом правого гвинта: за позитивний напрямок нормалі приймається напрямок поступального руху гвинта, головка якого обертається у напрямку струму, що тече в рамці (рис. 6.1).

Рис. 6.1

Досліди показують, що магнітне поле спричинє на рамку зі струмом орієнтовну дію, повертаючи її певним чином. За напрямок магнітного поля у даній точці приймається напрямок, уздовж якого розташована позитивна нормаль до рамки (рис. 6. 2).

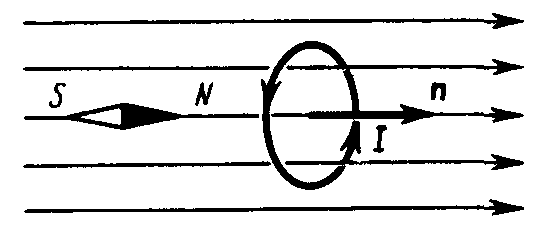
Рис. 6. 2

Рамкою зі струмом можна скористатися також і для кількісного опису магнітного поля. Якщо у дану точку магнітного поля помістити рамки з різними магнітними моментами, то на них діють різні обертаючі моменти, однак відношення (M_max - максимальний обертаючий момент) для всіх контурів одне і те ж, тому може служити характеристикою магнітного поля, що називається магнітною індукцією:

, (6.1)

- вектор магнітного моменту рамки зі струмом. Для плоского контура зі струмом I:

, (6. 2)

де S - площа поверхні контура (рамки), - одиничний вектор нормалі до по­верхні рамки.

Магнітна індукція в даній точці однорідного магнітного поля визначається максимальним обертаючим моментом, діючим на рамку з магнітним момен­том, що дорівнює одиниці, коли нормаль до рамки перпендикулярна напрямку поля.

Магнітне поле макрострумів описується вектором напруженості . Для однорід­ного ізотропного середовища вектор магнітної індукції пов’язаний з вектором напруженості таким співвідношенням:

(6. 3)

де ₀ - магнітна стала,  — безрозмірна величина — магнітна проникність середовищща, що показує, у скільки разів магнітне поле макрострумів H посилюється за рахунок поля мікрострумів середдовища.

Закон Біо - Савара - Лапласа для провідника зі струмом I, елемент dl якого створює у якійсь точці А (рис. 6. 3) індукцію поля , записується у вигляді:

(6. 4)

де - вектор, що за модулем дорівнює довжині dl елемента провідника та збігається за напрямком зі струмом, - радіус-вектор, проведений з елемента dl провідника у точку А поля, r - модуль радіус-вектора . Напрямокперпендикулярний до та , тобто перпендикулярний до площини, у котрій вони лежать, і збігається з дотичною до лінії магнитної індукції. Цей напрямок може бути знайдений за правилом правого гвинта: напрямок обертання головки гвинта дає напрямок, якщо поступальний рух гвинта відповідає напрямку струму в елементі.

Рис. 6. 3

Модуль вектора визначається виразом:

(6. 5)

де  — кут між векторами і .

1. Магнітне поле прямого струму, що тече по тонкому прямому проводу нескінченної довжини. У будь-якій точці, віддаленій від осі провідника на відстань R:

(6. 6)

2. Магнітне поле у центрі кругового провідника зі струмом визначається формулою:

(6. 7)

Зaкoн пoвнoгo струму для мaгнітногo пoля у вaкyyмі (тeopeмa прo циpкyляцію вeктopa ): циpкyляція вeктopa у будь-якому зaмкненoмy кoнтypі доpівнює добутку мaгнітнoї сталої₀ нa aлгeбpaїчнy cyмy струмів, oxоплениx цим кoнтypoм:

(6. 8)

дe - вeктop елeмeнтapнoї довжини кoнтypa, спрямованoї уздoвж oбxoду кoнтypa, B_l = Bcosa - cкладова вeктopa у нaпpямку дотичної до кoнтypа (з yрахуванням вибpaнoгo нaпpямку oбxoду), - кут між вeктopaми і , n — чиcлo пpoвідників зі струмaми, oxоплених кoнтypoм L будь-якої фopми.

Розглянемо соленоїд довжиною l, що має N витків, по котрому тече струм I. Довжину соленоїда вважаємо у багато разів більшою, ніж діаметр його витків. Всередині соленоїда поле є однорідним, зовні соленоїда - неоднорідним та дуже слабким.

На рис. 6. 4 репрезентовані лінії магнітної індукції всередині та зовні соленоїда. Чим соленоїд довший, тим менша магнітна індукція зовні його.

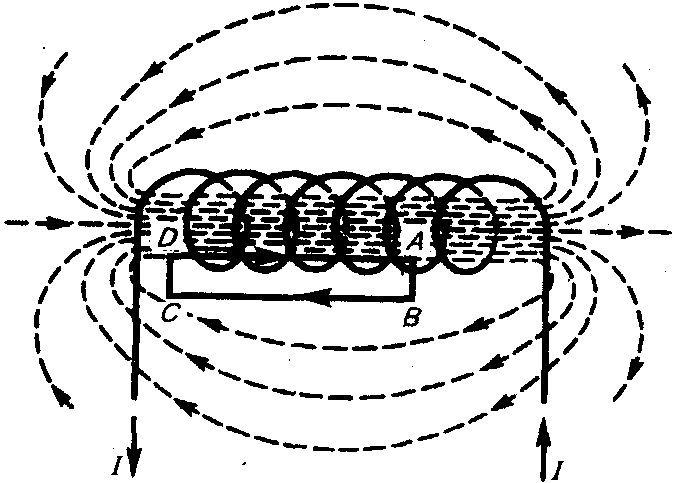
Рис. 6. 4. Магнітна індукція всередині соленоїда

Магнітна індукція всередині соленоїда має вигляд:

(6. 9)

де ₀ – магнітна стала.

Потік вектора магнітної індукції Ф_B через довільну поверхню S дорівнює:

(6. 10)

деB_n=Bcos- проекція вектора на напрямок нормалі до площі dS ( - кут між векторамита), - вектор, модуль якого дорівнює dS, а напрямок його збігається з напрямком нормалі до площі.

Для однорідного поля та плоскої поверхні, розташованої перпендикулярно вектору ,B_n = B = const і

_n = BS. (6. 11)

Одиницею магнітного потоку є вебер (Вб): 1 Вб - маг­нітний потік, що проходить крізь плоску поверхню площею 1 м², розташовану перпендикулярно однорідному магнітному полю, індукція якого дорівнює 1 Тл (1 Вб = 1 Тл  м²).

Магнітне поле чинить на рамку з током орієнтовну дію. Ампер встановив, що сила , з якою магнітне поле діє на елемент провідника dl зі струмом, що знаходиться у магніт­ному полі, дорівнює:

, (6.12)

де - вектор, що за модулем дорівнює dl та збігається за напрямком зї струмом, - вектор магнітної індукції.

Модуль сили Ампера обчислюється за формулою:

dF = IBdlsin , (6.13)

де  - кут між векторами і .

Рис. 6. 5

Якщо провідник не закріплений (наприклад , одна із сторін контура виготовлена у вигляді рухомої перемички, рис. 6. 5), тоді під дією сили Ампера провідник переміститься паралельно само собі на від­різок dx із стану 1 у стан 2. Робота, що здійснюється магнітним полем, дорівнює:

dА = Fdx = Ibldx = IbdS = IdФ. (6.14)

У останній формулі ldx = dS - площа, що перетинається провідником при його переміщенні у маг­нітному полі, ВdS = dФ - потік вектора магнітної індукції, що пронизує цю площу. Таким чином,

dA = IdФ. (6.15)

Проінтегруємо вираз (6.13) та визначимо роботу, що здійснюється силами Ампера:

А = IФ, (6.16)

тобто робота по переміщенню замкненого контура зі струмом у магнітному полі дорівнює добутку сили струму на зміну магнітного потоку, зчепленого з контуром.

Два паралельних струми однакового напрямку притягуються один до одного з силою:

(6.17)

Якщо струми мають протилежні напрями, тоді між ними діє сила відштовхування, що визначається формулою (6.17).

Сила , діюча на електричний заряд q, що рухається у магнітному полі зі швидкістю , називається силою Лоренца і виражається формулою:

F = qvBsin , (6.18)

де - індукція магнітного поля, у якому заряд рухається, - кут між та.

Рис. 6. 6

На рис. 6. 6 показана взаємна орієнтація векторів ,(поле спрямоване до нас, на рисунку показане крапками) і для позитивного заряду. На негативний заряд сила діє у протилежному напрямку.

Якщо заряджена частинка рухається у магнітному полі зі швидкістю , яка перпен­дикулярна вектору, тоді сила Лоренца постійна за модулем і нормальна до траєкторії частинки. Згідно з другим законом Ньютона, ця сила створює доцентро­ве прискорення. Звідси виходить, що частинка буде рухатися по колу, радіусr котрого визначається з умови qvB = mv²/r, звідки

(6.19)

Період обертання частинки, тобто час T, за який вона здійснює один повний оберт,

. (6. 20)

Підставивши сюди вираз (6.19), отримаємо

(6. 21)

тобто період обертання частинки в однорідному магнітному полі визначається тільки величиною, оборотною до питомого заряду (q/m) частинки, і магнітною індукцією поля, але не залежить від її швидкості (при v << c). На цьому грунтується дія циклічних прискорювачів заряджених частинок.

Прискорювачами заряджених частинок (циклотронами, фазотронами та ін.) називають пристрої, у яких під дією електричних та магнітних полів створюються і управляються жмутки високоенергетичних заряджених частинок (електронів, протонів, мезонів та ін.).

Ефект Хола (1879) - це виникнення у металі (чи напівпровіднику) зі струмом густиною , розташованому у магнітному полі , електричного поля у напрямку, перпендикулярному и . Електрони випробовують дію сили Лоренца (рис. 6. 7). У результаті між краями пластинки виникне поперечне електричне поле, направлене знизу угору. Коли напруженість Е_B цього попереч­ного поля досягне такої величини, що його дія на заряди буде врівноважувати силу Лоренца, тоді встановиться стаціонарний розподіл зарядів у поперечному напрямку. Тоді

eE_B = e /a = evB, или  = vBa,

де а - ширина пластинки,  - поперечна (холівська) різниця потенціалів.

Враховуючи, що сила струму I = jS = nevS (S - площа поперечного перерізу пластинкитовщиною d, п - концентрація електронів, v – середня швидкість упорядкованого руху електронів), отримаємо

Рис. 6. 7

У формулі R = 1/(en) - постійна Холла, що залежить від речовини.

Явище електромаг­нітної індукції виводиться з того, що у замкненому контурі при зміні потоку магнітної індукції, що охоплюється цим контуром, виникає електричний струм, який називається індукційним.

Значення індукційного струму і, відповідно, електрорушійної сили (е.р.с.) електро­магнітної індукції E_i визначається тільки швидкістю зміни магнітного потоку

(6. 22)

Знак мінус у формулі (6. 22) визначається правилом Ленца - загальним правилом для знаходження напрямку індукційного струму.

Правило Ленца: індукційний струм у контурі має завжди такий напрямок, що створене ним магнітне поле перешкоджає зміні магнітного потоку, який викликає цей індукційний струм.

Індукційний струм виникає не тільки у лінійних провідниках , але й у масивних суцільних провідниках, розташованих у змінному магнітному полі. Ці струми мають назву вихрових (інакше – струми Фуко). Вони викликають нагрівання провідників.

Електричний струм, що тече у замкненому контурі, створює навкруг себе магнітне поле, індукція якого, за законом Біо - Савара – Лапласа , пропорційна струму. Тому зчеплений з контуром магнітний потік Ф є пропорційним струму I у контурі:

Ф = LI, (6.23)

де коефіцієнт пропорційності L називається індуктивністю контура.

При зміні сили струму у контурі буде змінюватися також і зчеплений з ним магнітний потік; внаслідок чого у контурі буде виникати е.р.с. самоіндукції.

Із виразу (6. 23) визначається одиниця індуктивності генрі (Гн): 1 Гн - ин­дуктивність такого контура , магнітний потік самоіндукції якого при струмі у 1 А дорівює 1 Вб: 1 Гн = 1 Вб/А = 1 Вс/А.

Індуктивність нескінченно довгого соленоїда:

, (6. 24)

тобто індуктивність соленоїда залежить від числа витків соленоїда N, його довжини l, площі S та магнітної проникності  речовини, з якого виготовлене осердя соленоїда.

Е. р. с. самоіндукції

(6. 25)

де знак мінус, обумовлений правилом Ленца, показує, що наявність індуктив­ності у контурі приводить до уповільнення зміни струму у ньому.

Енергія магнітного поля, зв’язаного з контуром,

(6. 26)