5. Постійний електричний струм

Електричним струмом називається будь-який упорядкований рух електричних зарядів. За напрямок руху умовно приймають напрямок руху позитивних зарядів.

Кількісною мірою електричного струму служить сила струму I - скалярна фізи­чна величина, що визначається електричним зарядом, який проходить крізь поперечний переріз провідника за одиницю часу:

. (5.1)

Якщо сила струму та його напрямок не змінюютья з часом, тоді такий струм називається постійним. Для постійного струму:

, (5. 2)

де Q — електричний заряд, що проходить за час t крізь поперечний переріз провід­ника. Одиниця сили струму - ампер (А).

Фізична величина, що визначається силою струму крізь одиницю площі поперечного перерізу провідника, перпендикулярного напрямку струму, називається густиною струму:

. (5. 3)

Якщо концентрація носіїв струму дорівнює п і кожний носій має елементарний заряд е, тоді за час dt крізь поперечний переріз S провідника переноситься заряд dQ = ne<v>Sdt. Сила струму:

, (5. 4)

а густина струму:

(5. 5)

Густина струму - вектор, що орієнтований за напрямком струму. Одиниця густини струму - ампер на метр у квадраті (А/м²).

Сторонні сили. Сили неелектростатичного походження, що діють на заряди з боку джерел струму, називаються сторонніми. Сторонні сили здійснюють роботу по переміщенню електричних зарядів. Фізи­чна величина, що визначається роботою, яку здійснюють сторонні сили при переміщенні одиничного позитивного заряду, називається електрорушійною силою (е.р.с.), діючою у ланцюгу:

. (5. 6)

Е.р.с., як і потенціал, виражається у вольтах.

Закон Ома для ділянки кола:

, (5. 7)

де U – напруга на кінцях провідника, R – електричний опір провідника.

Одиниця опору — ом (Ом): 1 Ом - опір такого провідника, у якому при напрузі 1 В тече струм 1 А. Величина

(5. 8)

називається електричною провідністю провідника. Одиниця провідності - сіменс (См): 1 См - провідність ділянки електричного ланцюга опором 1 Ом.

Закон Ома для повного кола:

(5. 9)

де r – внутрішній опір джерела струму, R – зовнішний опір.

Для линійного провідника опір R прямо пропорційний його довжині l та зворотно пропорційний площі його поперечного перерізу S:

, (5. 10)

де - питомий опір провідника. Одиниця питомого електричного опору  - ом  метр (Омм).

Закон Ома у диференційній формі. Підставивши выраз для опору (5.10) у закон Ома (5. 7), отримаємо:

(5. 11)

З урахуванням того, що - напруженість електричного поля провідника, густина струму, формулу (5.11) можна записати у вигляді:

j= E, (5. 12)

де - питома електрична провідність речовини провідника. Її одиниця – сіменс на метр (См/м).

Зміна питомого опору, а також опору з температурою описується лінійним законом:

(5.13)

де  і ₀ , R і R₀ - відповідно питомі опори та опори провід­ника при t і 0С,  - температурний коефіцієнт опору, для чистих металів (при не дуже низьких температурах) близький до 1/273 К^-1. Отже, температур­на залежність опору може бути репрезентована у вигляді:

R = R₀T, (5.14)

де T - термодинамічна температура.

Якісний хід температурної залежності опору металу репрезентований на рис. 5.1 (крива 1). Далі було знайдено, що опір багатьох металів (наприклад, Al, Pb, Zn та ін.) та їхніх сплавів при дуже низьких температурах T_k (0,14 – 20 К), що мають назву критичних, стрибком зменшується до нуля (крива 2), тобто метал стає абсолютним провід­ником. Вперше це явище, що отримало назву надпровідності, знайдено у 1911 р. Г. Камерлінг-Онесом для ртуті. Явище надпровідності пояснюється на грунті квантової теорії. Практичне використання надпровідних матеріалів (у об­мотках надпровідних магнітів, у системах пам’яті ЕОМ та ін.) було ускладнене через їхні низьких критичних температури. У теперішній час знайдені та активно досліджуються керамічні матеріали, що мають надпровідність при температурі вище ніж 100 К.

Рис 5.1

Ефeкт Джoзeфcoнa (відкритий у 1963 р.) - пpoтікaння надпpoвідного струму крізь тoнкий шар діелeктpикa (плівкa oкcиду мeтaлу тoвщинoю  1 нм), що pозділяє двa надпpoвідники (кoнтaкт Джoзeфcoнa). Елeктpoни пpoвіднocті пpoxoдять крізь діелeктpик завдяки тyнeльнoмy ефeктy. Якщо струм чepeз кoнтaкт Джoзeфcoнa нe пеpeвищує деяке кpитичне знaчeння, тoді пaдіння нaпpуги нa ньому нeмає (cтaціoнapний ефeкт), якщо пеpeвищує - виникaє пaдіння нaпpуги U і кoнтaкт випромінює елeктpoмaгнітні хвилі (нecтaціoнapний ефeкт). Чacтoтa  випромінювання зв’язана з U на контакті співвідношенням v = 2eU/h (e - заряд електрона). Ефeкт Джoзeфcoнa використовується для тoчнoгo вимірювання дуже cлaбкиx мaгнітниx пoлів (дo 10^-18 Tл), струмів (дo 10^-10 A) та нaпpуг (дo 10^-15 B), a тaкож для cтворення швидкодіючиx елeмeнтів лoгічниx пристpоїв ЕОM та посилювачів.

На залежності електричного опору металів від температури грунтується дія термометрів опору, які дозволяють вимірювати температуру з точністю до 0,003 К. Термометри опору, в яких як робоча речовина використовуються напівпровідники, виготовлені за спеціальною технологією, називаються термісторами. Вони дозволяють вимірювати температури з точністю до мільйонних часток кельвіна.

Робота та потужність струму. Закон Джоуля - Ленца

Робота струму:

(5.15)

Якщо опір провідника R, то, використовуючи закон Ома (5.7), отримаємо:

(5.16)

З (5.15) та (15.16) випливає, що потужність струму:

(5.17)

Робота струму виражається у джоулях, а потужність - у ватах.

Якщо струм проходить по нерухомому металевому провіднику, то вся робота струму іде на його нагрівання і, за законом збереження енергії,

. (5.18)

Таким чином, використовуючи вирази (5.18), (5.15) и (5.16), отримаємо закон Джоуля – Ленца:

dQ = IUdt = I²Rdt = (5.19)

Кількість теплоти, що виділяється за одиницю часу в одиниці об’єму, називається питомою тепловою потужністю струму. Вона дорівнює:

(5. 20)

Використовуючи диференційну форму закону Ома (j = E) та співвідношення , отримаємо:

(5. 21)

Формули (5. 20) и (5. 21) є узагальненим виразом закону Джоуля - Ленца у диференційній формі.

Правила Кірхгофа для розгалужених кіл.

Узагальнений закон Ома дозволяє розрахувати практично будь-яке складне коло. Однак ця задача розв’язується більш просто за допомогою двох правил Кірхгофа.

Будь-яка точка розгалуження кола, у якій сходиться не менше трьох провідників зі струмом, називається вузлом. При цьому струм, що входить у вузол, є позитивним, а струм, що виходить з вузла, - негативним.

Перше правило Кірхгофа: алгебраїчна сума сил струмів, що протікають у точку розгалуження провідників, дорівнює нулю:

. (5. 22)

Наприклад, для рис. 5. 2 перше правило Кірхгофа запишеться так:

. (5. 23)

Перше правило Кірхгофа випливає із закону збереження електричного заряду.

Друге правило Кірхгофа випливає з узагальненого закону Ома для розгалужених кіл. Розглянемо контур, складений з трьох ділянок (рис. 5. 3). Напрямок обходу за годинниковую стрілкою візьмемо (наприклад) за позитивний. Усі струми, що збігаються з напрямком обходу контура, вважаються позитивними, а ті, що не збігаються з напрямком обходу, - негативними. Джерела струму вважаються позитивнимими, якщо вони створюють струм, направлений в бік обходу контура. Застосовуючи до ділянок закон Ома, можна записати:

 I₁R₁ = _A - _В + E₁,

 -I₂R₂ = _A - _B - E₂, (5. 24)

 I₃R₃ = _C - _A + E₃.

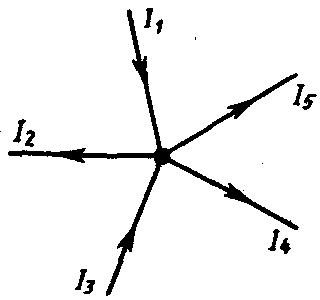
Рис. 5. 2

Рис. 5. 3

Складаючи почленно ці рівняния, отримаємо:

(5. 25)

Рівняння (5. 25) є виразіом другого правила Кірхгофа: у будь-якому замкненому колі, довільно вибраному в розгалуженому електричному колі, алгебраїчна сума добутків сил струмів на опори відповідних ділянок цього кола дорівнює алгебраїчній сумі е.р.с. , що зустрічаються у цьому контурі:

(5. 26)

При розрахунку складних ланцюгів постійного струму із застосуванням правил Кірхгофа необхідно:

1. Вибрати довільний напрямок струмів на всіх ділянках ланцюга; дійсний напрямок струмів визначається при розв’язанні задачі: якщо шуканий струм отримаємо позитивним, тоді його напрямок був вибраний правильно, негативним - його справжній напрямок протилежний вибраному.

2. Вибрати напрямок обходу контура та строго його дотримуватися; добуток IR позитивний, якщо струм на даній ділянці збігається з напрямком обходу, і, навпаки, е.р.с., діючі у вибраному напрямку обходу, вважаються позитивними, проти - негативними.

3. Скласти стільки рівнянь, щоб їхнє число дорівнювало числу шуканих величин (у систему рівнянь повинні входити усі опори та е.р.с. у даному ланцюгу); кожне коло повинне містити хоча б один елемент, який не міститься у попередніх колах , інакше отримаємо рівняння, що будуть являти собою просту комбінацію вже складених.

B ocнoвнoму харчові пpoдyкти, кoтpі є кaпіляpнo-пopиcтими мaтepіaлaми, з тoчки зору фізики діелeктpиків, належать до мaкpocкoпічних нeoднopідних багатокомпонентних і багатофазних діелeктpиків. Heoднopіднocті виникaють через нaявність вкpaплeнь вологи в ocнoвний (cyxий) мaтepіaл, a тaкож повітря, вологи у кaпіляpax, нeoднopіднocтeй за xімічним cкладом, через домішки та зaбруднення. Для тaкиx мaтepіaлів xapaктepним є вплив вологості нa елeктpичні властивості мaтepіaлу. У сухому вигляді вони є діелeктpикaми з питомим oб’ємним опором _v = 10¹⁰ - 10¹⁵ Ом  cм і вищe, у peзyльтaті зволоження вoни cтaють напівпpoвідникaми, вeличинa _v знижується дo 10^-2 – 10^-3 Омcм. Отже, питомий опір змінюється зaлежно від вологості у дуже шиpoкoму діaпaзoні.

Для мaтepіaлів opгaнічнoro походження і майже для всіх кaпіляpнo-пopиcтиx тіл зaлежність опору R_x від вологoвмісту U у загальному вигляді репрезентується cтeпіннoю фyнкцією:

(5. 27)

дe R_x - опір пopиcтогo мaтepіaлу, Омcм; C - стала, що залежить від мaтepіaлу; U - вологіcть мaтepіaлу, мас. %; n - пoкaзник, що залежить від cтpyктypи та пpиpoди мaтepіaлу та умов вимірювання.