Показники вирощування сільськогосподарських культур

Показник (із розрахунку на 1 га)	Озима пшениця	Цукрові буряки	Наявний ресурс
Затрати праці, людино-днів	5	25	270
Затрати праці механізаторів, людино-днів	2	8	80
Урожайність, тонн	3,5	40	—
Прибуток, тис. грн	0,7	1	—

Критерієм оптимальності є максимізація прибутку.

Запишемо економіко-математичну модель структури виробницт­ва озимої пшениці та цукрових буряків, ввівши такі позначення:

х₁ — шукана площа посіву озимої пшениці, га;

х₂ — шукана площа посіву цукрових буряків, га.

Задача лінійного програмування має такий вигляд:

max Z = 0,7x₁ + x₂(2.10)

за умов:

x₁ + x₂ ≤ 20;(2.11)

5x₁ + 25x₂ ≤ 270;(2.12)

2x₁ + 8x₂ ≤ 80;(2.13)

x₂ ≥ 5;(2.14)

x₁ ≥ 0, x₂ ≥ 0.(2.15)

Геометричну інтерпретацію задачі зображено на рис. 2.2.

Рис. 2.2. Область допустимих розв’язків задачі

Область допустимих розв’язків цієї задачі дістаємо так. Кожне обмеження, наприклад х₁ + х₂ 20, задає півплощину з граничною прямоюх₁ + х₂ = 20. Будуємо її і визначаємо півплощину, яка описується нерівністю х₁ + х₂ 20. З цією метою в нерівністьх₁ + х₂ 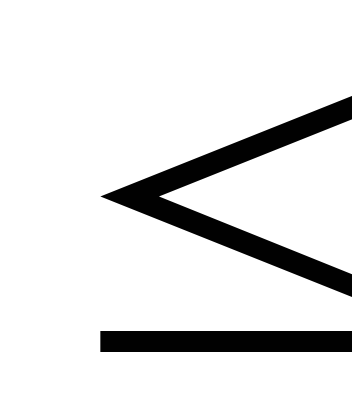20 підставляємо координати характерної точки, скажімо,х₁ = 0 і х₂ = 0. Переконуємося, що ця точка належить півплощині х₁ + х₂ 20. Цей факт на рис. 2.2 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (2.11)—(2.15). У результаті перетину цих півплощин утворюється область допустимих розв’язків задачі (на рис. 2.2 — чотирикутникABCD). Цільова функція Z = 0,7x₁ + x₂ являє собою сім’ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z = 0, то маємо 0,7х₁ + х₂ = 0. Ця пряма проходить через початок системи координат. Коли Z = 3,5, то маємо пряму 0,7х₁ + х₂ = 3,5.

2.5. Основні властивості розв’язків задачі лінійного програмування

Властивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем (доведення теорем та їх наслідки наведено нижче).

Властивість 1. (Теорема 2.2) Множина всіх планів задачі лінійного програмування опукла.

Властивість 2. (Теорема 2.3) Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’яз­ків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Властивість 3. (Теорема 2.4) Якщо відомо, що система векторівA₁, A₂, …, A_k(k ≤ n) у розкладі A₁x₁ +A₂x₂ + … + A_nx_n = A₀, X ≥ 0лінійно незалежна і така, що

A₁x₁ + A₂x₂ + … + A_kx_k = A₀,

де всі x_j ≥ 0,то точкаX = (x₁, x₂, …, x_k, 0, …, 0)є кутовою точкою багатогранника розв’язків.

Властивість 4. (Теорема 2.5) Якщо X = (x₁, x₂, …, x_n) — кутова точка багатогранника розв’язків, то вектори в розкладі A₁x₁ + + A₂x₂ + … + A_nx_n = A₀, X ≥ 0, що відповідають додатним x_j, є лінійно незалежними.

Доведемо сформульовані теореми.

Теорема 2.2. Множина всіх планів задачі лінійного програмування опукла.

Доведення. Необхідно довести, що коли X₁ та X₂ — плани задачі лінійного програмування (2.1)—(2.3), то їх опукла комбінація X = λ₁X₁ + λ₂X₂, λ₁ ≥ 0, λ₂ ≥ 0, λ₁ + λ₂ = 1 також є планом задачі.

Так як X₁ і X₂ — плани задачі, то виконуються такі співвідношення:

AX₁ = A₀, X₁ ≥ 0; AX₂ = A₀, X₂ ≥ 0.

Якщо підставити в систему обмежень значення X, то отримаємо:

AX = A(λ₁X₁ + λ₂X₂) = λ₁AX₁ + λ₂AX₂ = λ₁A₀ + λ₂A₀ = (λ₁ + λ₂)A₀ = A₀.

Отримали, що X задовольняє систему обмежень задачі лінійного програмування (2.2), і оскільки Х₁ ≥ 0, Х₂ ≥ 0, λ₁ ≥ 0, λ₂ ≥ 0, то й Х ≥ 0, тобто задовольняють і умову (2.3). У такий спосіб доведено, що Х — план задачі лінійного програмування.

Теорема 2.3. Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин багатогранника розв’язків. Якщо цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Д

Рис. 2.3. Багатокутник розв’язків задачі у двовимірному просторі

оведення. Припустимо, що багатогранник розв’язків задачі обмежений і має скінченну кількість кутових точок. Позначимо його через Q. У двовимірному просторі Q має вид багатокутника, що зображено на рис. 2.3. Позначимо кутові точки через Х₁, Х₂, ..., Х_р, а оптимальний план — Х₀.

Задача (2.1) — (2.3) розв’язується на максимум, отже, при будь-якому Х із Q для значення Х₀ виконується нерівність F(X₀) ≥ F(X). Якщо Х₀ — кутова точка, то перша частина теореми доведена. Припустимо, що Х₀ не є кутовою точкою, тоді Х₀ є точкою, яка належить опуклій множині (доведено в попередній теоремі). Отже, її можна подати як опуклу лінійну комбінацію кутових точок множини Q, тобто

X₀ = λ₁X₁ + λ₂X₂ + … + λ_pX_p,

.

У зв’язку з тим, що F(X) — лінійна функція, отримаємо:

(2.16)

У такому розкладі серед значень F(X_i) вибираємо найбільше (припустимо, що воно відповідає кутовій точці і позначимо його через m, тобто . Замінимо в (2.16) кожне значенняF(X_i) цим найбільшим значенням. Оскільки , то

.

За припущенням Х₀ — оптимальний план, отже, з одного боку, F(X₀) ≥ F(X_k) = m, а з другого, доведено, що F(X₀) ≤ m, значить, F(X₀) = m = F(X_k), де X_k — кутова точка. Отже, лінійна функція досягає максимального значення в кутовій точці (X_k).

Для доведення другої частини теореми припустимо, що F(X) набирає максимальних значень більше, ніж в одній кутовій точці, наприклад у точках Х₁, Х₂, ..., Х_q, (1 ≤ q ≤ p), тоді F(X₁) = F(X₂) = … = F(X_q) = m. Якщо Х опукла лінійна комбінація цих кутових точок, то:

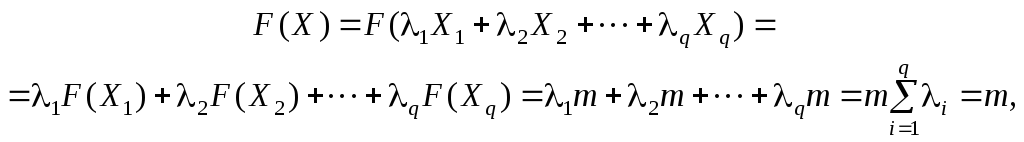
тобто лінійна функція F набирає максимальних значень у довільній точці Х, яка є опуклою лінійною комбінацією кутових точок Х₁, Х₂, ..., Х_q.

Зауваження. Якщо багатокутник розв’язків — необмежена область (рис. 2.4), то не кожну точку можна подати у вигляді опуклої лінійної комбінації її кутових точок. У такому разі задачу лінійного програмування з багатокутником розв’язків, що є необмеженою областю, можна звести до задачі з обмеженою областю, ввівши в систему додаткове обмеження х₁ + х₂ ≤ L, де L — достатньо велике число. Введення цього обмеження означає в

Рис. 2.4. Багатокутник розв’язку задачі у двовимірному просторі з необмеженою областю

ідтинання прямоюх₁ + х₂ = L від багатокутної необмеженої облас­ті обмеженого багатокутника, для якого виконується наведена теорема.

Очевидно, що координати кутових точок, які утворяться в результаті введення нового обмеження, залежать від L. Якщо в одній з них лінійна функція набирає максимального значення, то воно залежить від L. Змінюючи L, значення функціонала можна зробити як завгодно великим, а це означає, що лінійна функція необмежена на багатограннику розв’язків.

Теорема 2.4. Якщо відомо, що система векторів (k ≤ n) у розкладі ,лінійно незалежна і така, що

,

де всі x_j ≥ 0, то точка X = (x₁, x₂, …, x_k, 0, …, 0) є кутовою точкою багатогранника розв’язків.

Доведення. Припустимо, що точка Х не є кутовою. Тоді вона може бути виражена опуклою лінійною комбінацією двох інших точок Х₁ та Х₂ багатокутника розв’язків, тобто:

Компоненти векторів Х₁ та Х₂, значення λ₁ і λ₂ невід’ємні і останні n – k компонентів вектора Х дорівнюють нулю, тому відповідні n – k компонент векторів Х₁ та Х₂ також мають дорівнювати нулю, тобто

,

.

Оскільки Х₁ та Х₂ — плани, то

,

.

Віднімаючи від першого рівняння друге, отримаємо:

.

За припущенням вектори лінійно незалежні, тому останнє співвідношення виконується, якщо

.

Звідси:

Отже, Х неможливо подати як опуклу лінійну комбінацію двох інших точок багатокутника розв’язків. Значить, Х — кутова точка.

Теорема 2.5. Якщо — кутова точка багатогранника розв’язків, то вектори в розкладі,, що відповідають додатним, є лінійно незалежними.

Доведення. Не порушуючи загальності, можна вважати нерівними нулю перші k елементів вектора Х, отже,

.

Здійснимо доведення від супротивного. Припустимо, що система векторів лінійно залежна. Тоді існують такі числа, не всі рівні нулю, за яких виконується співвідношення:

.

За умовою

.

Задамо деяке число , помножимо на нього першу рівність, далі результат спочатку додамо до другого, а потім віднімемо від другого рівняння:

,

.

Отже, система рівнянь задачі лінійного програмування має два розв’язки, які можуть і не бути планами.

.

Всі х_і > 0, тому число можна вибрати настільки малим, що всі перші компонентитанабуватимуть додатних значень, тодіта— плани. При цьому, тобтоХ — опукла лінійна комбінація точок Х₁ та Х₂, що суперечить умові теореми, оскільки Х — кутова точка.

Припущення стосовно лінійної залежності векторів привело до суперечності. Отже, воно є неправильним, а система векторів — лінійно незалежна.

Наслідок 1. Оскільки вектори мають розмірністьm, то кутова точка багатокутника розв’язків має не більше, ніж m додатних компонентів .

Наслідок 2. Кожній кутовій точці багатокутника розв’язків відповідає лінійно незалежних векторів системи.

З наведених властивостей можна висновувати:

якщо функціонал задачі лінійного програмування обмежений на багатограннику розв’язків, то:

1. існує така кутова точка багатогранника розв’язків, в якій лінійний функціонал досягає свого оптимального значення;

2. кожний опорний план відповідає кутовій точці багатогранника розв’язків.

Тому для розв’язання задачі лінійного програмування необхідно досліджувати лише кутові точки багатогранника (опорні плани), не включаючи до розгляду внутрішні точки множини допустимих планів.

2.6. Графічний метод розв’язування задач лінійного програмування

Для розв’язування двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Обмежене використання графічного методу зумовлене складністю побудови багатогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе.

Розглянемо задачу.

Знайти

(2.17)

за умов:

(2.18)

. (2.19)

Припустимо, що система (2.18) за умов (2.19) сумісна і багатокутник її розв’язків обмежений.

Згідно з геометричною інтерпретацією задачі лінійного програмування (§ 2.4) кожне і-те обмеження-нерівність у (2.18) визначає півплощину з граничною прямою (і = 1, 2, …, т). Системою обмежень (2.18) графічно можна зобразити спільну частину, або переріз усіх зазначених півплощин, тобто множину точок, координати яких задовольняють всі обмеження задачі — багатокутник розв’язків.

Умова (2.19) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометрично інтерпретується як сім’я паралельних прямих с₁х₁ + с₂х₂ = const.

Скористаємося для графічного розв’язання задачі лінійного програмування властивостями, наведеними в § 2.5:

якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатокутника розв’язків. Якщо ж цільова функція досягає екстремального значення більш як в одній вершині багатокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.

Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (2.17) лінійна цільова функція набуває найбільшого (найменшого) значення.

Алгоритм графічного методу розв’язування задачі лінійного програмування складається з таких кроків:

1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі (2.18) знаків нерівностей на знаки рівностей.

2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.

3. Знаходимо багатокутник розв’язків задачі лінійного програмування.

4. Будуємо вектор , що задає напрям зростання значення цільової функції задачі.

5. Будуємо пряму с₁х₁ + с₂х₂ = const, перпендикулярну до вектора .

6. Рухаючи пряму с₁х₁ + с₂х₂ = const в напрямку вектора (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального зна- чення.

7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.

У разі застосування графічного методу для розв’язування задач лінійного програмування можливі такі випадки:

1. Цільова функція набирає максимального значення в єдиній вершині А багатокутника розв’язків (рис. 2.5).

2. Максимального значення цільова функція досягає в будь-якій точці відрізка АВ (рис. 2.6). Тоді задача лінійного програмування має альтернативні оптимальні плани.

3. Задача лінійного програмування не має оптимальних планів: якщо цільова функція необмежена згори (рис. 2.7) або система обмежень задачі несумісна (рис. 2.8).

Рис. 2.5 Рис. 2.6

Рис. 2.7 Рис. 2.8

4. Задача лінійного програмування має оптимальний план за необмеженої області допустимих розв’язків (рис. 2.9 і 2.10). На рис. 2.9 у точці В маємо максимум, на рис. 2.10 у точці А — мінімум, на рис. 2.11 зображено, як у разі необмеженої області допус­тимих планів цільова функція може набирати максимального чи мінімального значення у будь-якій точці променя.

Рис. 2.9 Рис. 2.10

Р

Рис. 2.11

озв’язувати графічним методом можна також задачі лінійного програмуванняn-вимірного простору, де , якщо при зведенні системи нерівностей задачі до системи рівнянь шляхом введення додаткових змінних кількість зміннихn на дві більша, ніж число обмежень m, тобто .

Тоді, як відомо з курсу вищої математики, можна дві з n змінних, наприклад х₁ та х₂, вибрати як вільні, а інші m зробити базис­ними і виразити через вільні. Припустимо, що це зроблено. Отримаємо рівнянь вигляду:

Оскільки всі значення , то мають виконуватись умови:

,

(2.19.1)

Розглянемо, як можна зобразити ці умови геометрично. Візьмемо, наприклад, першу з них:

Узявши величину х₃ рівною своєму крайньому значенню — нулю, отримаємо рівняння:

.

Це рівняння прямої. Для такої прямої , по одну сторону від неї, а по другу —. Відмітимо ту сторону прямої, де.

В аналогічний спосіб побудуємо і всі інші обмежуючі прямі: ;;...;і відмітимо для кожної з них півплощину, де відповідна змінна більше нуля.

У такий спосіб отримують n – 2 прямі та дві осі координат (,). Кожна з них визначає півплощину, де виконується умова . Частина площини вналежить водночас всім півплощинам, утворюючи багатокутник допустимих розв’язків.

Припустимо, що в задачі необхідно знайти максимальне значення функціонала:

.

Підставивши вирази для ,,, ...;з (2.19.1) у цей функціонал, зведемо подібні доданки і отримаємо вираз лінійної функ­ції F всіх n змінних лише через дві вільні змінні та:

,

де — вільний член, якого в початковому вигляді функціонала не було.

Очевидно, що лінійна функція досягає свого максимального значення за тих самих значеньта, що й. Отже, процедура відшукання оптимального плану з множини допустимих далі здійснюється за алгоритмом для випадку двох змінних.

Розв’язати графічним методом задачу лінійного програмування

.

Розв’язання. Маємо n = 7 — кількість змінних, m = 5 — кількість обмежень. Виберемо як вільні змінні х₁ та х₂ і виразимо через них всі інші базисні змінні. З першого рівняння маємо:

(2.19.2)

З третього рівняння:

, (2.19.3)

а з четвертого:

. (2.19.4)

Підставляючи (2.19.2) в друге рівняння системи і (2.19.4) в останнє, розв’язуємо їх відносно х₄ та х₇. Отримаємо:

;

.

Далі за алгоритмом беремо х₁ = 0 та х₂ = 0 — координатні осі; інші обмежуючі прямі знаходимо, узявши х₃ = 0, х₄ = 0, х₅ = 0, х₆ = 0, х₇ = 0. Багатокутник допустимих розв’язків зображено на рис. 2.12.

Рис. 2.12

Знайдемо вигляд функціонала, вираженого через х₁ та х₂. Для цього знайдені щойно вирази для х₃, х₄, х₅, х₆ та х₇ через вільні змінні х₁ і х₂ підставимо у функціонал і, звівши подібні члени, отримаємо: . Відкидаючи вільний член, маємо:. Будуємо вектор(–5, –2), перпендикулярно до нього — пряму F^'. Рухаючи пряму F^' в напрямку, протилежному (необхідно знайти мінімальне значення функціїF), отримаємо точку мінімуму — А (рис. 2.13).

Рис. 2.13

У точці А перетинаються дві обмежуючі прямі: х₆ = 0 та х₇ = 0. Отже, для відшукання її координат необхідно розв’язати систему рівнянь:

Розв’язком системи є = 8,5;= 5. Підставивши ці значення у відповідні вирази, знайдемо оптимальні значення базисних змінних:

= 0,5; = 16,5;= 17,5;= 0;= 0.

Підстановкою значень тав лінійну функціюF отримуємо значення цільової функції:

.

2.7. Приклади розв’язування задач графічним методом

Розглянемо застосування графічного методу для розв’язуван­ня деяких економічних задач.

Фірма спеціалізується на виробництві офісних меблів, зокрема вона випускає два види збірних книжкових полиць — А та В. Полиці обох видів виготовляють на верстатах 1 та 2. Тривалість обробки деталей однієї полиці кожної моделі подано в табл. (2.4).

Таблиця 2.4