метрология / пр / Метрология - Практика 7. Расчет делителей напряжения и тока

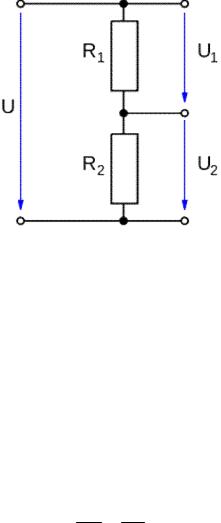
Практическая работа №7

Расчет делителей напряжения и тока.

Теоретические сведения

Делители напряжения. Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора R1 и R2,

подключённых к источнику напряжения U. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа.

Рис. 7.1. Схема резистивного делителя напряжения.

Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

U I R

Для каждого резистора имеем:

U1 I R1

U2 I R2

Разделив выражение для U1 на выражение для U2 в итоге получаем:

U1 R1

U2 R2

Таким образом, отношение напряжений U1 и U2 в точности равно отношению сопротивлений R1 и R2.

Далее

Откуда:

Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя,

так, чтобы в расчетах этим сопротивлением, включенным параллельно R2 можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 и больше раз по величине), потребляемого нагрузкой, но,

однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U. Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R=R1+R2. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, сумма величин близка расчетной.

При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений,

диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов – она должна превышать выделяемую на них мощность.

Стандартный ряд сопротивлений: 1,0; 1,1; 1,2; 1,3; 1,5; 1,6; 1,8; 2,0; 2,2; 2,4; 2,7; 3,0; 3,3; 3,6; 3,9; 4,3; 4,7; 5,1; 5,6; 6,2; 6,8; 7,5; 8,2; 9,1.

Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД)

режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. На практике это невозможно, поскольку, увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов:

электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.

Делители тока. Простейший резистивный делитель тока — это два параллельно включённых резистора R1 и R2, подключённых к источнику напряжения U. Поскольку резисторы соединены параллельно, то к ним приложено одинаковое напряжение.

Рис. 7.2. Схема резистивного делителя тока.

Ток через них можно определить согласно закону Ома:

I1 U

R1

I2 U

R2

Общий ток в цепи согласно первому закону Кирхгофа:

I I1 I2

Для поддержания приемлемой точности работы делителя, необходимо, чтобы величина тока, протекающего через сопротивления делителя, была не менее чем в

10 раз больше, чем ток, протекающий в нагрузке (см. аналогичное требование у делителя напряжения). Увеличение этого показателя (до ×100,×1000 или больше)

пропорционально увеличивает точность работы делителя, однако это также увеличивает поперечное сечение проводников, что увеличивает размеры,

стоимость и снижает КПД схемы. Это одна из причин, по которой делители тока малопригодны в качестве источников постоянного тока для питания нагрузок.

Для этой цели применяют иные схемотехнические решения, например стабилизаторы тока.

Примеры решения задач. Для делителя напряжения определить:

1. Выходное напряжение Uвых по известным значениям входного напряжения Uвх и сопротивлений резисторов R1, R2 :

Пример: Необходимо определить выходное напряжение Uвых делителя при известных напряжении источника тока Uвх = 50 В, и значениях R1 = 10 кОм и

R2 = 500 Ом.

Решение: По формуле вычисляем Uвых = 50 * 500 / (10000 + 500) = 2,38 В.

2. Входное напряжение делителя Uвх, по известным значениям выходного напряжения Uвых и сопротивлений резисторов R1, R2:

Пример: Необходимо определить входное напряжение Uвх делителя при необходимых выходном напряжении Uвых=4 В, и значениях R1=15 кОм и

R2=3 кОм.

Решение: По формуле вычисляем Uвх = 4 * (15000 + 3000) / 3000 = 24 В.

3. Значение R1 по известным значениям входного напряжения Uвх,

выходного напряжения Uвых и сопротивления резистора R2:

Пример: С помощью делителя напряжения необходимо получить на нагрузке сопротивлением 50 кОм напряжение Uвых = 10 В от источника напряжением

Uвх = 50 В.

Решение: Сопротивление резистора R2 должно быть в 100 раз меньше сопротивления нагрузки 50 кОм. Выполняем это условие: R2 = 500 Ом.

По формуле вычисляем R1 = 50 * 500 / 10 – 500 = 2000 Ом = 2 кОм.

Сам делитель потребляет ток от источника тока, в соответствии с законом Ома: Iдел = Uвх / (R1 + R2) = 50/(2000+500) = 0,02 А (20 мА).

Определим рассеиваемую мощность резисторов:

для резистора R1 : P = 0,02 * 0,02 * 2000 = 0,8 Вт;

для резистора R2 : P = 0,02 * 0,02 * 500 = 0,2 Вт.

4. Значение R1 и R2 по известным значениям входного напряжения Uвх,

выходного напряжения Uвых и входного (общего) сопротивления делителя Rобщ,

где Rобщ = R1 + R2:

Пример: Определить значения R1 и R2 делителя напряжения, если их сумма

R1+R2 = 1кОм, при входном напряжении источника Uвх = 50 В и напряжении на выходе Uвых = 20 В.

Решение: вычисляем R2 = 20 * 1000 / 50 = 400 Ом;

вычисляем R1 = 1000 - 400 = 600 Ом;

Сам делитель потребляет ток от источника тока, в соответствии с законом Ома: Iдел = Uвх / (R1 + R2) = 50/(600+400) = 0,05 А (50 мА).

Определим рассеиваемую мощность резисторов:

для резистора R1 : P = 0,05 * 0,05 * 600 = 1,5 Вт;

для резистора R2 : P = 0,05 * 0,05 * 400 = 1 Вт.

Для делителя тока определить:

1. Определить ток I1 и I2 в плечах резисторов R1, R2 по известным значениям общего тока Iобщ и сопротивлений резисторов R1, R2:

Пример: Определить значения I1 и I1 делителя тока, если значение общего тока Iобщ = 0,6А, сопротивление R1 =100 Ом, а R2 = 20 Ом.

Решение: вычисляем : I1 = 0,6 * 20 / (100 + 20) = 0,1 А;

вычисляем : I2 = 0,6 * 100 / (100 + 20) = 0,5 А;

резисторы поглощают мощность: P = I * I * R;

рассеиваемая мощность резисторов:

для резистора R1: P = 0,1 * 0,1 * 100 = 1 Вт;

для резистора R2: P = 0,5 * 0,5 * 20 = 5 Вт.

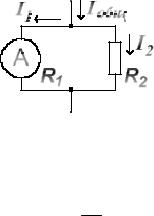
2. Рассчитать шунт R2 в цепи измерительного прибора, при известных:

внутреннем сопротивлении R1, максимальном токе обмотки катушки прибора I1 и

максимальном значении общего тока Iобщ цепи делителя тока, представленного на схеме:

Пример: Полное отклонение стрелки миллиамперметра при значении I1 = 1

мА, внутреннее сопротивление катушки прибора R1 = 200 Ом. Рассчитайте шунт

R2, чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.

Решение: вычисляем: R2 = 0,001 * 200 / (1 – 0,001) = 0,2 Ом;

поглощаемая (рассеиваемую) мощность R2: P = I2 * I2 * R2,

где I2 = Iобщ - I1 = 999 мА, P = 0,999 * 0,999 * 0,2 = 0,199 Вт.

Для достижения точности в измерительных цепях, выбирают высокоточные резисторы, кроме того, используют их последовательное и параллельное соединение.