метрология / пр / Метрология - Практика 5. Расчет мостов постоянного тока

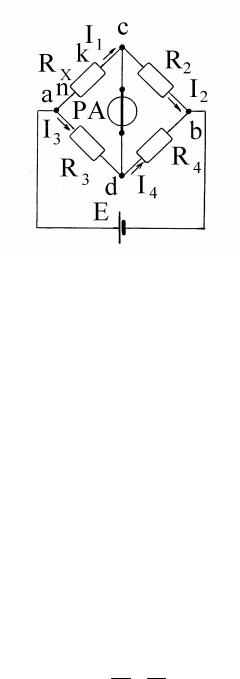
Практическая работа №5

Расчет одинарных и двойных мостовых схем измерений.

Цель работы: измерение величины активного сопротивления экспериментальным путем с помощью схемы одинарного моста.

Теоретические сведения

Для измерения средних сопротивлений используют одинарный мост постоянного тока (рис.5.1).

Рис. 5.1. Схема измерения средних сопротивлений одинарным мостом постоянного тока.

В одно плечо моста включают резистор с измеряемым сопротивлением Rx ,

а в три других плеча – резисторы c известными регулируемыми сопротивлениями

R2 , R3 , R4 . К диагонали ab моста подключен источник питания Е, а к диагонали cd – магнитоэлектрический гальванометр РА.

Д ля измерения величины Rx сопротивления R2 , R3 и R4 подбирают так,

чтобы ток через гальванометр был равен нулю. В этом случае потенциалы точек с и d одинаковы (φc = φd), то есть мост находится в равновесии. При этом I1 I2 ;

I3 I4 и Rx I1 R3 I3 ; R2 I2 R4 I4 .

Разделив последние два уравнения одно на другое, получим:

Rx R3

R2 R4

или

Rx R2 R3

R4

Полученное выражение называется уравнением равновесия моста.

Если измеряемое сопротивление Rx мало, то при включении его в схему моста на рис.5.1 возникает погрешность вследствие влияния сопротивлений соединительных проводов an и kc, а также переходных сопротивлений контактов

включением средних сопротивлений четырех зажимное включение резисторов с малым сопротивлением (рис.5.2).

Рис. 5.2. Схема измерения малых сопротивлений одинарным мостом постоянного тока.

Здесь цифрами 1 и 4 обозначены токовые зажимы, а цифрами 2 и 3 –

потенциальные зажимы резистора Rx. Сопротивления соединительных проводов

(an и kc на рис.5.1) не влияют на точность измерения, так как в схеме на рис.5.2

они включены в диагонали моста.

Более точные измерения малых сопротивлений в лабораторных условиях выполняют с помощью двойного моста.

Анализ работы схемы двойного моста (рис.5.3) удобнее выполнять,

предварительно заменив треугольник сопротивлений R3 , R4 , R5 на эквивалентную звезду (рис.5.4).

Рис. 5.3. Схема измерения средних сопротивлений двойным мостом.

Преобразованная схема (рис.5.4) представляет собой четырехплечий мост

(аналогичный одинарному мосту).

Рис. 5.4. Преобразованная схема двойного моста.

Мост уравновешен при условии:

R1 R0 Rb R2 RX Ra .

Здесь сопротивления Ra и Rb определяются выражениями:

Ra R3 R5 / R3 R4 R5 ;

Rb R4 R5 / R3 R4 R5 .

Подстановка этих выражений в уравнение равновесия моста дает:

R1 R0 R4 R5 / R3 R4 R5 R2 RX R3 R5 / R3 R4 R5 ;

следовательно

RX R2 R3 R4 R5 R1 R0 R3 R4 R5 R1 R4 R5 R2 R3 R5,

RX R1 R0 / R2 R4 R5 R1 / R2 R3 / R4 / R3 R4 R5 ,

окончательно:

RX R1 R0 / R2 R4 R5 R1 / R2 R3 / R4 / R3 R4 R5 .

При выполнении условия R1 / R2 R3 / R4 второе слагаемое последнего уравнения обращается в ноль и измеряемое сопротивление определяется по упрощенной формуле:

RX R1 R0 / R2.

Для того чтобы неточность выполнения равенства R1 / R2 R3 / R4 не давала заметной погрешности, сопротивление R5 соединительного провода должно быть достаточно малым, а сопротивления R1, R2, R3, R4, наоборот, должны быть большими (по крайней мере, не меньше 10 Ом), что позволяет исключить погрешности, обусловленные сопротивлениями соединительных проводов схемы.

При RX=10-5… 10-6 Ом погрешность при измерении с помощью двойного моста не превышает ± 1%, а при измерении сопротивлений RX>10-3 Ом погрешность не превышает ± 0,05%.

Примеры решения задач:

1. Определить неизвестное сопротивление Rx в схеме одинарного моста постоянного тока, если R2=10 Ом, R3=75 Ом, R4=50 Ом.

Решение: Rx R2 R3

R4

Rx 10 75 15

50

2. Определить значения регулируемого сопротивления R2, если измеряемое сопротивление может находиться в пределах (10-3000) Ом, R3=50 Ом, R4=1000 Ом.

Решение: R2MIN RxMIN R4 , R2MAX RxMAX R4

R3 R3

R2MIN 10 1000 200 Ом, 50

R2MAX 3000 1000 60 103 Ом 50

3. Определить значения регулируемого сопротивления R4, если измеряемое сопротивление может находиться в пределах (10-3000) Ом, R2=900 Ом, R3=1000 Ом.

R4MAX 900 1000 90 103 Ом. 10

4. Определить ток потребления одинарной мостовой измерительной схемы с гальванометрическим измерительным прибором, если R2=400 Ом, R3=600 Ом, R4=4800 Ом, E=5 В.

Rx 400 600 50 Ом, 4800

RX,3 Rx R3

Rx R3

50 600

RX ,3 50 600 46,15 Ом,

R2,4 R2 R4 ,

R2 R4

400 4800

R2,4 400 4800 369,23 Ом,

RСУМ RX ,3 R2,4 ,

RСУМ 46,15 369,23 415,38 Ом,

5. Определить ток потребления одинарной мостовой измерительной схемы с измерительным вольтметром, если R2=400 Ом, R3=600 Ом, R4=4800 Ом, E=5 В.

R3,4 600 4800 5400 Ом,

RСУМ RX,2 R3,4

RX,2 R3,4

450 5400

RСУМ 450 5400 415,38,