Газовые процессы в ts− диаграмме.

1. Изотермический процесс.

При изотермическом процессе T=const. Поэтому TS− диаграмме он изображается прямой линией, параллельной оси абсцисс.

С учетом того, что dT=0, зависимости изменения энтропии идеального газа в изотермическом процессе примут вид

(1)

(уходит слагаемое в правой части)

(2)

Выражение для энтропии идеального газа через T,V (1) Tp (2) pV (3)

Процесс 1-2 – это процесс, в котором энтропия увеличивается, а следовательно, к газу подводится теплота и газ совершает работу расширения, эквивалентную этой теплоте.

Процесс2-1− это процесс сжатия, в котором теплота, эквивалентная работе сжатия, отводится от газа и энтропия уменьшается

Площадь фигуры S₁12 S₂ соответствует количеству теплоты q, сообщаемому газу, и одновременно работе l (изотермический процесс)

2. Адиабатный процесс

В адиабатном процессе q=0 и dq=0, а следовательно dS=0.

Следовательно, в адиабатном процессе S=const и в TS − диаграмме адиабатный процесс изображается прямой линией, параллельной оси T.

Поскольку в адиабатном процессе S=const,то адиабатные обратимые процессы называют также изоэнтропными.

При адиабатном сжатии температура рабочего тела повышается, а при расширении понижается. Поэтому процесс1-2 – это процесс сжатия, а процесс 2-1 – это расширение.

Из уравнения

(3)

При k=const получим

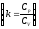
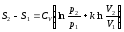
или

(*)

Для обратимого адиабатного процесса S₁=S₂=const, тогда из (*)

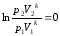
Откуда,

− уравнение адиабаты в координатах p и V.

3. Изохорный процесс

Для изохорного процесса V=const, dV=0.

При постоянной теплоемкости (из ур. (1))

− вид на TS – диаграмме

Подкасательная к кривой процесса в любой её точке определяет значение истинной теплоёмкости C_V.

Подкасательная будет положительной только в том случае, если кривая будет обращена выпуклостью вниз.

Площадь под кривой процесса 1-2 на TS – диаграмме дает в масштабе количество подведенной (или отведенной в процессе 2-1) теплоты q, равное изменению внутренней энергии U₂-U₁.

4. Изобарный процесс

В изобарном процессе давление постоянное p=const

В этом случае

из (2)

Следовательно, при p=const как и при V=const изобара является логарифмической кривой, поднимается следа направо и обращена выпуклостью вниз.

Подкасательная к кривой 1-2 в любой её точке дает значения истинной теплоёмкости C_p.

Площадь под кривой дает кол-во теплоты q, которая сообщается газу при p=const, равное изменению энтальпии i₂-i₁.

5. Политропный процесс

В политропном процессе.Теплоёмкость в этом процессе

Тогда,

Отсюда, для конечного изменения состояния газа

Политропный процесс на TS – диаграмме изображается кривой, расположение которой зависит от показателя n.

6. Круговой процесс. Цикл Карно.

Изобразим в TS – диаграмме произвольный обратимый цикл 1a2b1.

В процессе 1a2 рабочее тело получает кол-во теплоты q₁, численно равное площади под кривой 1a2, а в процессе 2-b-1 отдает кол-во теплоты q₂, численно равное площади под кривой 2-b-1.

Часть теплоты

переходит в работу цикла l (∆u=0 в цикле).

Работа цикла положительна, если цикл проходит по часовой стрелке и отрицательна, если против часовой стрелки (направление цикла в pV и TS − диаграммах одинакова).

Термический к.п.д. кругового процесса

Изменение энтропии в любом цикле равно нулю.

Цикл Карно состоит из двух изотерм и двух адиабат. В TS – диаграмме он будет изображаться в виде прямоугольника (горизонтальные линии – изотермы, вертикальные – адиабаты)

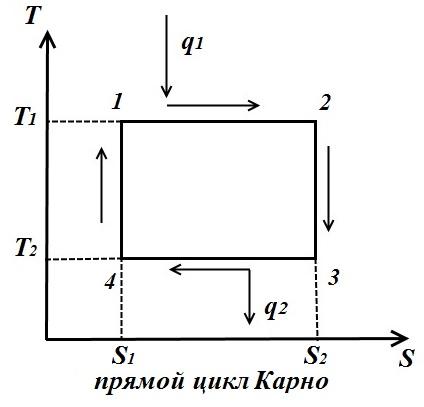
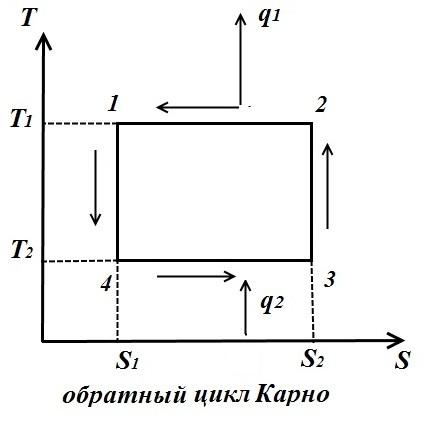
Количество теплоты, подведенное к рабочему телу, числено равно площади прямоугольника 12S₂S₁:

Количество теплоты, отведенное к холодильнику, соответствует площади прямоугольника 34S₁S₂:

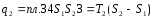
Теплота, эквивалентная работе цикла, равная площади цикла

Термический к.п.д. цикла

Для обратного цикла (рис. справа)

Холодильный коэффициент обратного цикла