2.3.2. Динаміка твердого тіла та системи тіл

Приклад 1. Вказати правильну відповідь.

Якщо на диск (рис.23) масоюm = 10 кг і радіусом R= 0,4 м діє момент сил опору М_оп = 2 Н·м, то обертальний рух диска відбувається з кутовим прискоренням, яке за абсолютним значенням становить:

1)| ε | = 1,8 рад/с²;

2)| ε | = 2,5 рад/с²;

3)| ε | = 1,5 рад/с²;

4)| ε | = 3,6 рад/с².

Розв’язання. Щоб відповісти на питання прикладу, треба скористуватися основним рівнянням динаміки обертального руху тіла навколо нерухомої осі: ТутI_Z– момент інерції тіла відносно осі обертанняz, що спрямована в даному випадку перпендикулярно до площини малюнка і проходе через центр мас диска – точкуС;ε– кутове прискорення тіла;

–сума моментів усіх сил, що діють на тіло, відносно осі обертання. Тоді кутове прискорення тіла визначається за формулою

.

До суми моментів усіх сил відносно осі обертання надходить лише момент сил опору, так як інші сили, що діють на тіло в процесі руху (сила ваги , сили , – складові реакції нерухомого шарніраC), моментів відносно осі обертання не створюють, так як перетинають цю вісь (проходять через ось):

Формула для обчислення I_z – моменту інерції суцільного однорідного диска відносно центральної осі, має вигляд:

,

де m– маса диска,R– його радіус.

Підставимо дані в наведені формули і получимо чисельний результат:

Н·м; кг·м²;

рад/с².

Отже, з наведених в прикладі відповідей правильною буде відповідь 2).

Приклад 2. Вказати правильну відповідь.

Якщо механічна система ( рис. 24 ) складається із вантажівА масою m_А = 10 кг та D масою m_D = 4 кг і ступінчастого диску В з радіусом інерції ρ_в = 0,4м ( R_В = 0,5м ; r_В = 0,2м ) і масою m_В = 5 кг , то при значенні швидкості тіла А V_A = 2м/c кінетична енергія системи дорівнює:

1) Т ^сист = 100 Dж;

2) Т ^сист = 110 Dж;

3) Т ^сист = 120 Dж;

4) Т ^сист = 130 Dж.

Розв’язання. В даному прикладі розглядається рух механічної системи, що складається із трьох тіл (тіла А, В і D), які зв’язані між собою тросами. В процесі переміщення системи ці троси не розтягуються. Треба визначити кінетичну енергію заданої системи в тому її положенні, коли швидкість тілаА приймає значення V_A = 2м/c.

Кінетична енергія системи дорівнює арифметичній сумі кінетичних енергій усіх тіл і точок системи і в даному випадку становить

,

де ,,− кінетичні енергії відповідно тілА,ВіD системи.

Кінетична енергія тіла залежить не тільки від його швидкості і маси, але ще й від виду руху. Тому при визначенні треба враховувати вид руху кожного тіла системи і, крім того, швидкості усіх тіл системи в даному прикладі слід виражати через задану швидкість V_A.

Тіло А рухаєтьсяпоступальнов процесі переміщення системи, тому його

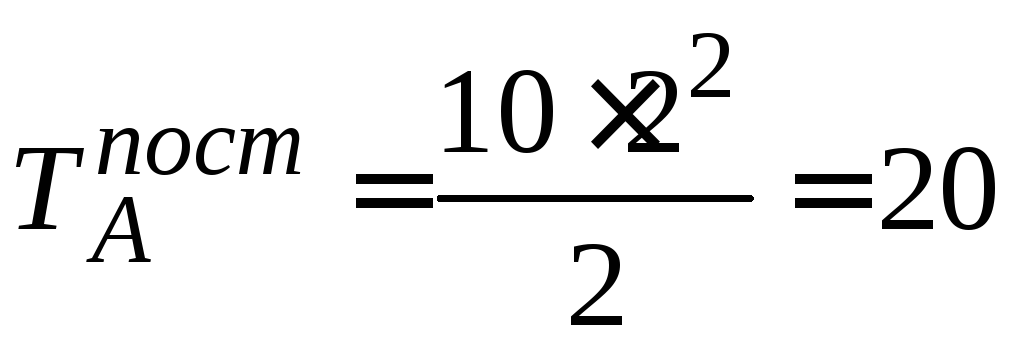кінетична енергія обчислюється за формулою і при підстановці чисельних даних приймає значенняDж.

Тіло (ступінчастий диск ) виконує обертальнийрух відносно центральної осіz_с, що проходе перпендикулярно до площини малюнка через центр мас диска (точку С); тому кінетична енергія диска обчислюється за формулою, де− момент інерції дискавідносно центральної осіz_с, а− його кутова швидкість.

Момент інерції ступінчастого диска відносно центральної осі обчислюється за формулою , де− маса диска, а− його радіус інерції відносно центральної осі. При підстановці чисельних даних момент інерції приймає значення.

Кутову швидкість треба виразити через задану швидкістьV_A:

рад/с.

Тоді кінетична енергія тіла приймає значення:

Dж.

Тіло D системи, як і тілоА, рухаєтьсяпоступально, тому його кінетична енергія обчислюється за аналогічною формулою.

Швидкість V_DтілаDтреба визначити через задану швидкістьV_Aіз співвідношення.

Тоді м/с і кінетична енергія тілаD приймає значення: Dж.

В результаті кінетична енергія системи буде наступна:

Dж.

Із 4-ох відповідей, наведених у прикладі, правильною буде відповідь2).

Приклад 3. Вказати правильну відповідь (прискорення вільного падіння g прийняти рівним 10 м/с²).

Якщо маси тіл системи (рис. 25) та радіуси диска В мають відповідно значення m_A = 15 кг, m_В = 6 кг, m_D = 4 кг ; R_B = 0,5м, r_B = 0,2м, а коефіцієнт тертя тіла А становить µ_А= 0,4, то сумарна робота зовнішніх сил, що діють на систему на переміщенні S_A = 2м, становить:

1) = + 72,4Н·м;

2) = − 33,6Н·м;

3) = + 48,8Н·м;

4) = − 20,3Н·м.

Розв’язання. В даному прикладі розглядається рух механічної системи, що складається із трьох тіл (тілаА,ВіD), які зв’язані між собою тросами; в процесі переміщення системи троси не розтягуються. Треба визначити сумарну роботу зовнішніх сил, що діють на систему на заданому переміщенніS_A =2м.

До зовнішніх сил, що діють на систему в процесі руху, відносяться усі сили, що зображені на рис. 25: активні сили− сили ваги тіл, ,;реакції зовнішніх в’язей − складові реакції площини,; складові реакції нерухомого шарніра , .

Однак треба зауважити, що не усі зовнішні сили виконують роботу. Так сили ,,прикладені до точкиС, яка не переміщується в процесі руху системи, тому їх робота дорівнює нулю:, так як. Сила спрямована перпендикулярно до напрямку переміщення тілаА , тому робота її теж дорівнює нулю:, так як.

Із наведених сил тільки три сили будуть виконувати роботу: сили ваги тіл ,і сила тертя, що прикладена до тілаА − . Ці сили сталі за величиною істалі занапрямком по відношенню до переміщень точок їх прикладення, а робота таких сил обчислюється за спрощеним правилом: робота сталої сили дорівнює добутку модуля сили на переміщення точки прикладення сили і на косинус кута між напрямком сили і напрямком переміщення.

Таким чином, в даному прикладі сума робіт зовнішніх сил буде складатися із трьох доданків: .

Сила прикладена до центра ваги тілаА і виконує роботу на заданому переміщенніS_A. Кутα між напрямком сили і напрямком переміщення становить 60⁰, так як сила ваги діє донизу по вертикалі, а переміщення точки прикладення сили відбувається униз по площині, про що свідчить напрямок вектора швидкості на рис.25. Тому робота сили обчислюється за формулою:.

Оскільки в умові прикладу задаються маси тіл системи, то величину сили ваги треба виразити через масу тілаA і прискорення вільного падінняg, яке по умові прикладу слід приймати рівним 10 м/с² (). Тоді робота сили приймає значення: Н·м.

Сила тертя теж прикладена до тілаА і виконує роботу на заданому переміщенніS_A. Ця сила завжди діє у бік, протилежний до переміщення, тобто створює з напрямком переміщення кут. Тому робота сили тертя обчислюється за формулою:

.

Значення сили тертя відповідає виразу , де величину нормальної складової реакції площини треба обчислити за формулою

H.

Тоді сила тертя буде дорівнювати H, а робота сили тертя приймає значенняН·м.

Сила прикладена до центра ваги тіла D і виконує роботу на переміще-нні центра ваги цього тіла S_D. Кутα між напрямком сили і напрямком переміщення становить 180⁰, так як сила ваги діє по вертикалі униз, а переміщення тілаDвідбувається по вертикалі уверх, про що свідчить напрямок вектора швидкості на рис.25. Тому робота сили обчислюється за формулою

.

Переміщення S_Dтреба виразити через переміщенняS_A, встановивши між ними кінематичний зв'язок, аналогічний зв’язку між швидкостями:

і .

Із останнього співвідношення випливає, що м і робота сили становить Н·м.

Тоді сума робіт зовнішніх сил приймає значення:

Н·м.

Із наведених в прикладі відповідей правильною буде відповідь 3).