Статично невизначувані задачі на розтягання (стискання)

1. Визначити напруження в стержні (рис. 51) при підвищенні його температури на Δt =50°, якщо a =0,4 м, b =0,8 м, Δ =0,5 мм, коефіцієнти лінійного розширення для сталі α_ст =1,25·10^-5, для міді α_м =1,65·10^-5; модуль пружності сталі Е_ст = 2·10⁵ МПа, міді Е_м = 10⁵ МПа.

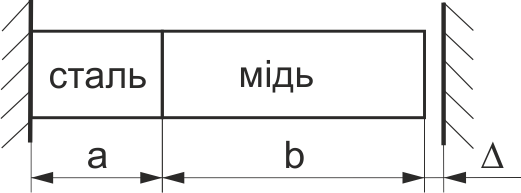
Рис. 51.

2. Визначити напруження в стержні (рис. 52) при його нагріванні на Δt =70°, якщо коефіцієнти лінійного розширення для сталі α_ст =1,25·10^-5, для міді α_м=1,65·10^-5; модуль пружності сталі Е_ст =2·10⁵ МПа, міді Е_м=10⁵ МПа.

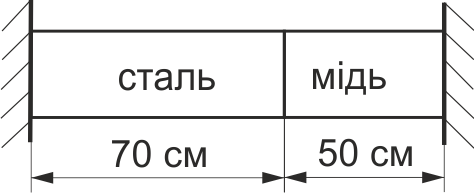
Рис. 52.

3. Визначити, з якою силою буде тиснути стержень (рис. 52) на нерухомі, абсолютно жорсткі стінки при нагріванні стержня на Δt =70°, якщо площа перерізу стержня А = 40см², коефіцієнти лінійного розширення для сталі α_ст =1,25·10^-5, для міді α_м =1,65·10^-5; модуль пружності сталі Е_ст=2·10⁵ МПа, міді Е_м =10⁵ МПа (рис. 52)

4. Визначити, з якою силою буде тиснути сталевий стержень (рис. 53)на нерухомі, абсолютно жорсткі стінки, якщо його нагріти на Δt =40°. Площа перерізу лівої частини стержня А₁ =10 см², площа перерізу правої частини А₂ =20 см², коефіцієнт лінійного розширення для сталі α_ст=1,25·10^-5, модуль пружності Е=2·10⁵ МПа.

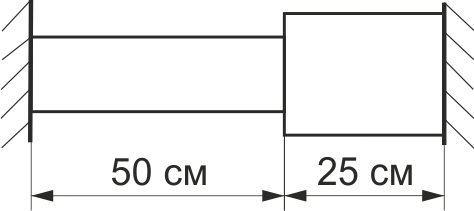
Рис. 53.

5. Визначити напруження в лівій частині стержня (рис. 53), якщо його нагріти на Δt =40°. Площа перерізу лівої частини стержня А₁ =10 см², площа перерізу правої частини А₂ = 20 см², коефіцієнт лінійного розширення сталі α_ст =1,25·10^-5, модуль пружності Е = 2·10⁵ МПа.

6. Визначити напруження в правій частині стержня (рис. 53), якщо його нагріти на Δt =40°. Площа перерізу лівої частини стержня А₁ =10 см², площа перерізу правої частини А₂ = 20 см², коефіцієнт лінійного розширення сталі α_ст =1,25·10^-5, модуль пружності Е =2·10⁵ МПа .

7. Сталевий стержень (рис. 54), затиснутий з двох боків, навантажено силою F. Визначити напружено-деформований стан в стержні ліворуч та праворуч від перерізу, де прикладена сила.

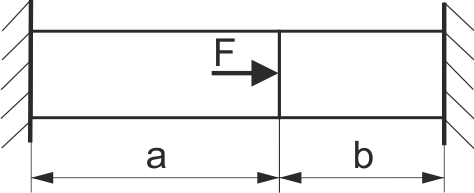
Рис. 54.

8. Визначити напруження в стержні (рис. 55) ліворуч від перерізу, в якому прикладена сила, якщо F = 200 кН, А = 20 см², модуль пружності сталі Е_ст =2·10⁵ МПа, міді Е_м =10⁵ МПа.

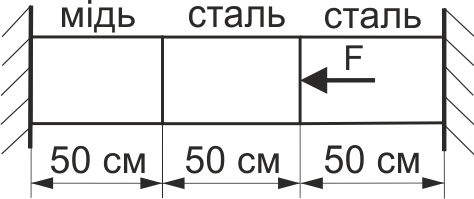
Рис. 55.

9. Визначити напруження в стержні (рис. 55) праворуч від перерізу, в якому прикладена сила, якщо F = 200 кН, А = 20 см², модуль пружності сталі Е_ст = 2·10⁵ МПа, міді Е_м = 10⁵ МПа.

10. Визначити реакцію R₁ в лівій стінці при дії на стержень (рис. 56) сили F=200 кН, якщо площа поперечного перерізу стержня А = 20 см², модуль пружності сталі Е_ст = 2·10⁵ МПа, міді Е_м =10⁵ МПа.

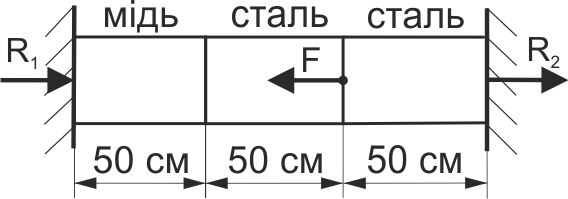
Рис. 56.

11. Визначити реакцію R₂ в правій стінці при дії на стержень (рис. 56) сили F=200 кН, якщо площа поперечного перерізу стержня А = 20 см², модуль пружності сталі Е_ст = 2·10⁵ МПа, для міді Е_м = 10⁵ МПа.

12. Визначити стискаюче напруження в лівій частині сталевого стержня (рис. 57), якщо F = 80 кН, площа перерізу лівої частини А₁ = 20 см², площа перерізу правої частини А₂ = 30 см².

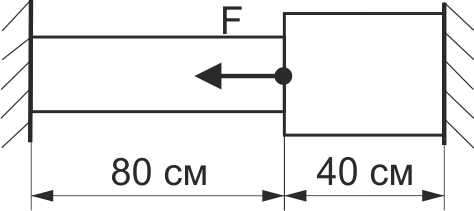
Рис. 57.

13. Визначити напруження в правій частині сталевого стержня (рис. 57), якщо F=80 кН, площа перерізу лівої частини А₁ = 20 см², площа перерізу правої частини А₂ = 30 см².

14. Визначити реакцію R₁ в лівій стінці при дії на стержень (рис. 58) сили F=80 кН, якщо площа перерізу лівої частини стержня А₁ = 20 см², площа перерізу правої частини А₂ = 30 см².

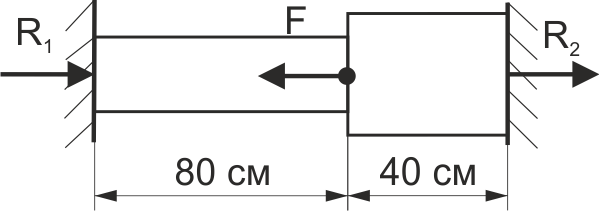
Рис. 58.

15. Визначити реакцію R₂ в правій стінці при дії на стержень (рис. 58) сили F=80 кН, якщо площа перерізу лівої частини стержня А₁ =20 см², площа перерізу правої частини А₂ = 30 см².

16. Визначити напруження в правій частині сталевого стержня (рис. 59), якщо F=90 кН, площа перерізу стержня А = 20 см².

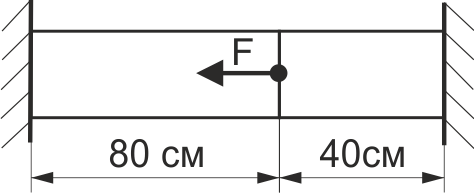
Рис. 59.

17. Визначити напруження в лівій частині сталевого стержня (рис. 59), якщо F=90 кН, площа перерізу стержня А = 20 см².

18. Визначити реакцію R₂ в правій стінці при дії на стержень (рис. 60) сили F=90 кН.

Рис. 60.

19. Визначити реакцію R₁ в лівій стінці при дії на стержень (рис. 60) сили F=90 кН.

20. Визначити напруження в правій частині сталевого стержня (рис. 61), якщо зазор між лівою стінкою та стержнем Δ = 0,1 мм, площа перерізу стержня А = 8 см².

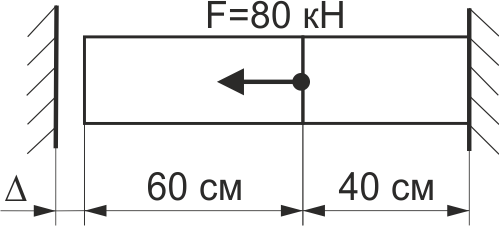
Рис. 61.

21. Визначити напруження в лівій частині сталевого стержня (рис. 61), якщо зазор між лівою стінкою та стержнем Δ = 0,1мм, площа перерізу стержня А = 8 см².

22. Визначити реакцію R₁ в лівій стінці при дії на сталевий стержень (рис. 62) сили F, якщо зазор між лівою стінкою та стержнем Δ = 0,1 мм, площа перерізу стержня А = 8 см².

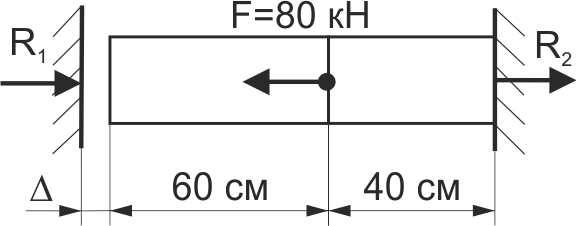
Рис. 62.

23. Визначити реакцію R₂ в правій стінці при дії на сталевий стержень (рис. 62) сили F, якщо зазор між лівою стінкою та стержнем Δ = 0,1 мм, площа перерізу стержня А = 8 см².

24. Абсолютно жорстка балка спирається на три бетонні колони (рис. 63) Е_б=1,5·10⁴ МПа однакового поперечного перерізу А = 600 см². Між балкою та середньою колоною до навантаження був зазор Δ = 0,6 мм. Знайти поздовжню силу в середній колоні.

Рис. 63.

25. Абсолютно жорстка балка спирається на три бетонні колони (рис. 63) Е_б=1,5·10⁴ МПа однакового поперечного перерізу А = 600 см². Між балкою та середньою колоною до навантаження був зазор Δ = 0,6 мм. Знайти напруження в середній колоні.

26. Абсолютно жорстка балка спирається на три бетонні колони (рис. 63) Е_б=1,5·10⁴ МПа однакового поперечного перерізу А = 600 см². Між балкою та середньою колоною до навантаження був зазор Δ = 0,6 мм. Знайти напруження в крайніх колонах.

27. Абсолютно жорстка балка спирається на три бетонні колони (рис. 63) Е_б=1,5·10⁴ МПа однакового поперечного перерізу А = 600 см². Між балкою та середньою колоною до навантаження був зазор Δ = 0,6 мм. Знайти величину стискання середньої колони.

28. Абсолютно жорстка балка спирається на три бетонні колони (рис. 64) Е_б=1,5·10⁴ МПа однакового поперечного перерізу А = 600 см². Між балкою та середньою колоною до навантаження був зазор Δ = 0,6 мм. Знайти величину опускання балки АВ.

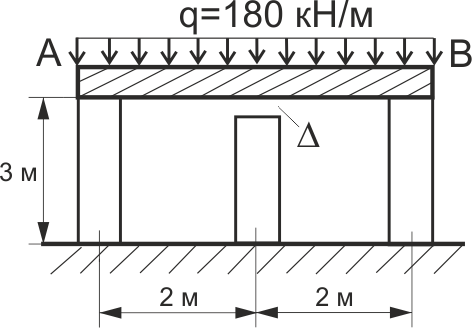
Рис. 64.