3. Геометрическая интерпретация двойного интеграла

Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью , снизу плоскостью и сбоку цилиндрической поверхностью, с образующей параллельной осиOz вырезающей на плоскости xOy область D, вычисляется по формуле:

Вчастности, если, объем цилиндрического тела численно равен площади областиD:

Пример 1. Вычислить гдеD –треугольник с вершинами O(0;0); A(1;1); B(2; 0).

Р

Рис.5

ешение. При выборе порядка интегрирования в этом примере, заметим, что подынтегральная функция легко интегрируется по любой переменной, но верхняя граница области (ломанная OAB) не описывается одной функцией, в то время как левая граница OA и правая AB описываются уравнениями прямых: Выбираем (2) способ:

Пример 2.

Вычислить область D – прямоугольник, ограниченный прямыми

Решение. Здесь порядок интегрирования диктует подынтегральная функция, которая легче интегрируется по x, значит, внутренний интеграл будет по x:

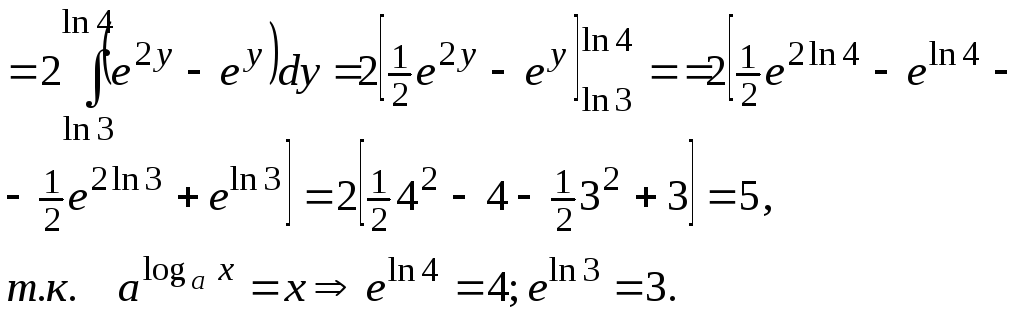
Пример 3. Нарисовать тело, объем которого описывается интегралом . Объем вычислить.

Решение. Основание тела, область D, описывается неравенствами , сверху тело ограничено поверхностью. Делаем чертежи. ОбластьD:и– половины парабол,– плоскость, параллельная осиOy, на плоскости хOy () оставляет след. Тело, объем которого V, изображен на рисунке:

2. Криволинейные интегралы

1. Криволинейный интеграл II рода по координате

Криволинейный интеграл II рода по координате записывается в виде

При условии, что непрерывны в точках дуги MN, а дуга – гладкая кривая , интеграл существует и вычисляется как определенный интеграл по формуле:

.

Кроме обычных свойств интеграла отметим, что

Если путь интегрирования простая замкнутая кривая L, то его обозначают , вычисляют в направлении против часовой стрелки и называютциркуляцией.

2.Физический смысл криволинейного интеграла II рода

Криволинейный интеграл II рода численно равен работе, которую совершает переменная сила на криволинейном путиMN.

Пример. Найти работу силы при перемещении по линии от точки к точке.

Решение.

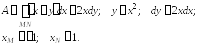
3. Связь между двойными и криволинейными интегралами.

Формула Грина

Пусть L граница односвязной области D. и их частные производные непрерывны в замкнутой областиD (включая ее границу L), то имеет место формула: .

Пример. Вычислить криволинейный интеграл двумя способами: непосредственно и по формуле Грина. L – контур треугольника ABCA .

Решение. 1. Вычислим непосредственно криволинейный интеграл:

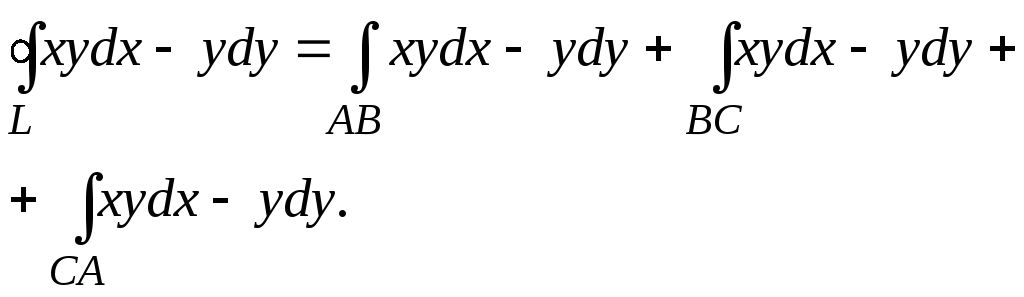
(BC) – прямая, проходящая через 2 точки, имеет уравнение:

.

.

2. Вычисление интеграла по формуле Грина:

Итак, мы получили тот же результат:

Индивидуальные задания

1 — 10. Найти неопределенные интегралы, в примерах а —­ б результаты интегрирования проверить дифференцированием.

1. а) , б), в),

г) , д), е).

2. а) , б), в),

г) , д), е).

3. а) , б), в),

г) , д), е).

4. а) , б), в),

г) , д), е).

5. а) , б), в),

г) , д), е).

6. а) , б), в),

г) , д), е).

7. а) , б), в),

г) , д), е).

8. а) , б), в),

г) , д), е).

9. а) , б), в),

г) , д), е).

10. а) , б), в),

г) , д), е).

11 — 20. Найти интегралы, используя метод интегрирования по частям.

11. a) , б) .

12. а) , б).

13. а) , б).

14. а) , б).

15. а) , б).

16. а) , б).

17. а) , б).

18. а) , б).

19. а) , б).

20. а) , б).

21 — 30. Проинтегрировать рациональные функции.

21. a) , б).

22. а) , б).

23. а) , б).

24. а) , б).

25. а) , б).

26. а) , б).

27. а) , б).

28. а) , б).

29. а) , б).

30. а) , б).

31 — 40. Найти интегралы от тригонометрических функций.

31. а) , б), в).

32. а) , б), в).

33. а) , б), в).

34. а) , б), в).

35. а) , б), в).

36. а) , б), в).

37. а) , б), в).

38. а) , б), в).

39. а) , б). в).

40. а) , б), в).

41 — 50. Найти интегралы с помощью подстановок.

41. а) , б), в).

42. а) , б), в).

43. а) , б), в).

44. а) , б), в).

45. а) , б), в).

46. а) , б), в).

47. а) , б), в).

48. а) , б), в).

49. а) , б), в).

50. а) , б), в).

51 — 60. Вычислить определенные интегралы:

51. а) , б), в) .

52. а) , б) , в) .

53. а) , б) , в) .

54. а) , б) , в) .

55. а) , б) , в) .

56. а) , б) , в) .

57. а) , б) , в) .

58. а) , б) , в) .

59. а) , б) , в) .

60. а) , б) , в) .

61 — 70. Найти общий интеграл дифференциального уравнения.

61. .	62. .
63. .	64. .
65. .	66. .
67. .	68. .
69. .	70. .

71 — 80. Проинтегрировать уравнение.

71. .	72. .
73. .	74. .
75. .	76. .
77. .	78. .
79. .	80. .

81 — 90. Найти частное решение дифференциального уравнения.

81.	,	,	.
82.	,	,	.
83.	,	,	.
84.	,	,	.
85	,	,	.
86.	,	,	.
87.	,	,	.
88.	,	,	.
89.	,	,	.
90.	,	,	.

91 — 100. Найти частное решение дифференциального уравнения.

91.	,	,	.
92.	,	,	.
93.	,	,	.
94.	,	,	.
95.	,	,	.
96.	,	,	.
97.	,	,	.
98.	,	,	.
99.	,	,	.
100.	,	,	.

101 — 110. Найти общее решение дифференциального уравнения.

101. . a),б).

102. . a),б).

103. . a),б).

104. . a),б).

105. . a),б).

106. . a),б).

107. . a),б).

108. . a),б)

109. . a),б).

110. . a),б).

111 — 120. Найти общее решение дифференциального уравнения.

111. .	112. .
113. .	114. .
115. .	116. .
117. .	118. .
119. .	120. .

121 — 130. Вычислить двойной интеграл.