
- •Математика
- •3 Семестр
- •3. Интегрирование методом подведения функции под знак дифференциала
- •4. Интегралы
- •5. Интегрирование рациональных дробей
- •6. Интегрирование тригонометрических функций
- •7. Метод интегрирования по частям
- •8. Метод подстановки
- •9. Определенный интеграл
- •§ 2. Дифференциальные уравнения
- •1. Уравнения первого порядка
- •1. Основные понятия
- •2. Уравнения с разделяющимися переменными
- •3. Линейные дифференциальные уравнения
- •2. Уравнения второго порядка
- •1. Основные определения
- •2. Уравнения вида
- •3. Уравнения второго порядка, не содержащие искомой функции
- •4. Уравнения второго порядка, не содержащие независимой переменной
- •5. Линейные уравнения второго порядка
- •2) Если то (II.V)
- •§ 3. Кратные и криволинейные интегралы
- •1. Двойные интегралы
- •1. Общие понятия
- •Геометрическая интерпретация двойного интеграла
- •Пример 2.
- •2. Криволинейные интегралы
- •121. .
- •Издательство «Нефтегазовый университет»
- •625000, Г. Тюмень, ул. Володарского, 38
- •625000, Г. Тюмень, ул. Володарского, 38
8. Метод подстановки
Справедливо
равенство
![]() ,
где
,
где![]() –дифференцируемая функция. После
вычислений интеграла надо сделать
обратную подстановку
–дифференцируемая функция. После
вычислений интеграла надо сделать
обратную подстановку![]() .
Конечно, этим методом целесообразно
пользоваться, если после подстановки
интеграл упрощается.
.
Конечно, этим методом целесообразно
пользоваться, если после подстановки
интеграл упрощается.
Пример
1. Найти интеграл![]()
Решение.
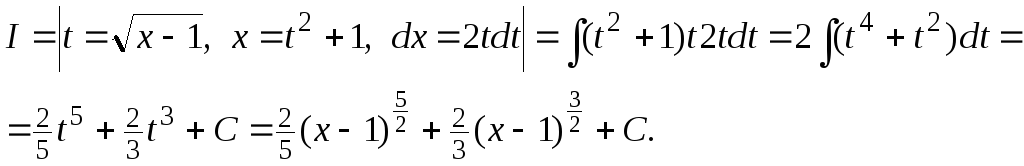
Выбор подстановки требует определенного опыта и искусства, но для некоторых классов функций можно дать рекомендации.
1. Интегрирование линейных иррациональностей
![]() где R
– рациональная
функция своих аргументов. Интеграл
сводится к интегрированию рациональной
дроби подстановкой
где R
– рациональная
функция своих аргументов. Интеграл
сводится к интегрированию рациональной
дроби подстановкой
![]() где
где![]()
Пример
2. Найти интеграл
![]()
Решение.
![]()
![]()
![]()
2. Интегрирование квадратичных иррациональностей. Тригонометрические подстановки
Интегралы
вида
![]() ,
,![]() ,
,![]() приводятся к интегралам от рациональной
функции относительно
приводятся к интегралам от рациональной
функции относительно![]() с помощью надлежащей тригонометрической
подстановки: для первого интеграла
с помощью надлежащей тригонометрической
подстановки: для первого интеграла![]() ,
для второго
,
для второго![]() и для третьего
и для третьего![]() .
.
Пример
3. Найти интеграл
![]()
Решение.
![]()
![]()
![]()

Пример
4. Найти интеграл
![]()
Решение.
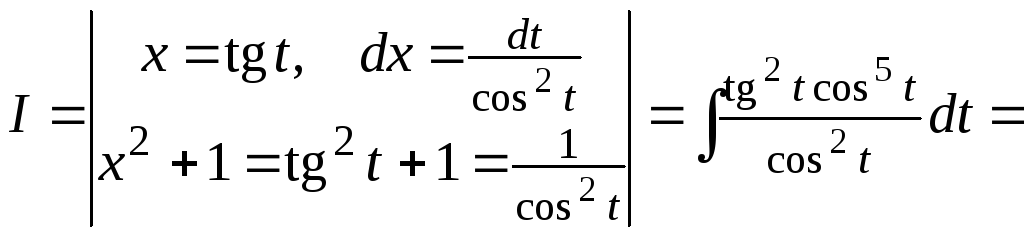
![]()
 .
.
3. Универсальная
тригонометрическая подстановка
![]()
Под интегралом
имеем рациональное выражение относительно
![]() и
и![]() .
Такие интегралы приводятся к интегралам
от рациональных функций с помощью
универсальной тригонометрической
подстановки
.
Такие интегралы приводятся к интегралам
от рациональных функций с помощью
универсальной тригонометрической
подстановки![]() .
В этом случае:
.
В этом случае:![]()
Пример
5. Найти интеграл
![]()
Решение.

![]()
9. Определенный интеграл
Пусть
![]() — функция, определеннаяна
отрезке
— функция, определеннаяна
отрезке
![]() ,
и пусть
,
и пусть
![]()
![]() —n
+ 1 точек, таких, что
—n
+ 1 точек, таких, что
![]() ,
кроме того, пусть
,
кроме того, пусть![]() ,
,![]()
![]() для всехk
= 1.. n.
Тогда сумма
для всехk
= 1.. n.
Тогда сумма
![]()
называется
интегральной
суммой.
Определенным
интегралом от
функции
![]() на отрезке
на отрезке![]() называется предел интегральной суммы
при условии, что длина наибольшего из
элементарных отрезков стремится к нулю:
называется предел интегральной суммы
при условии, что длина наибольшего из
элементарных отрезков стремится к нулю:
![]()
Если функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
то определенный интеграл существует.
,
то определенный интеграл существует.
Числа
![]() соответственно называютсянижним
и
верхним пределами интегрирования.
соответственно называютсянижним
и
верхним пределами интегрирования.
Основные свойства определенного интеграла
1.
![]()
2.
 где
где![]() постоянная.
постоянная.
3.
 4.
4.
5. Если
![]() –
нечетная функция, т.е.
–
нечетная функция, т.е.![]() то
то
Если
![]() – четная
функция,
т.е.
– четная
функция,
т.е.
![]() то
то
10. Геометрический смысл определенного интеграла
 Если
Если![]() на отрезке
на отрезке![]() ,
то определенный интеграл
,
то определенный интеграл численно равен площади криволинейной
трапеции, ограниченной графиком функции
численно равен площади криволинейной
трапеции, ограниченной графиком функции![]() ,
прямыми:
,
прямыми:![]() ,
,![]() и
и![]() .
.
Если
![]() меняет знак на отрезке
меняет знак на отрезке![]() ,
то
,
то дает алгебраическую сумму площадей
фигур, ограниченных линиями
дает алгебраическую сумму площадей
фигур, ограниченных линиями![]() ,
,![]() ,
,![]() ,
,![]() .
Причем площади, расположенные выше оси
.
Причем площади, расположенные выше оси![]() ,
входят в эту сумму со знаком плюс, а
площади, расположенные ниже оси
,
входят в эту сумму со знаком плюс, а
площади, расположенные ниже оси![]() ,
– со знаком минус.
,
– со знаком минус.
11. Методы вычислений
Формула Ньютона-Лейбница
Если
![]() –
некоторая первообразная для функции
–
некоторая первообразная для функции![]() ,
то определенный интеграл может быть
вычислен по формуле Ньютона-Лейбница:
,
то определенный интеграл может быть
вычислен по формуле Ньютона-Лейбница:
 .
.
Эта формула устанавливает связь между неопределенным и определенным интегралами.
Примеры. Вычислить интегралы.
1.

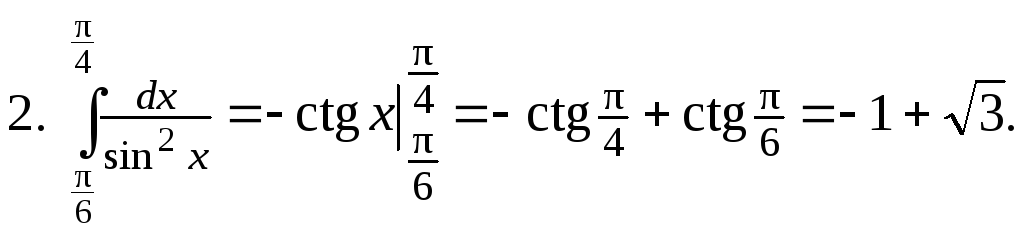
Замена переменных в определенном интеграле
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
а функция
,
а функция![]() дифференцируема
на отрезке
дифференцируема
на отрезке![]() ,
причем
,
причем![]() ,
,![]() ,
то
,
то
![]()
Обратите внимание, при замене переменной в определенном интеграле меняют пределы интегрирования, а к старым переменным не возвращаются.
Примеры. Вычислить интегралы.
1.
![]()
![]() .
.
2.
 .
.
3.

3. Интегрирование по частям
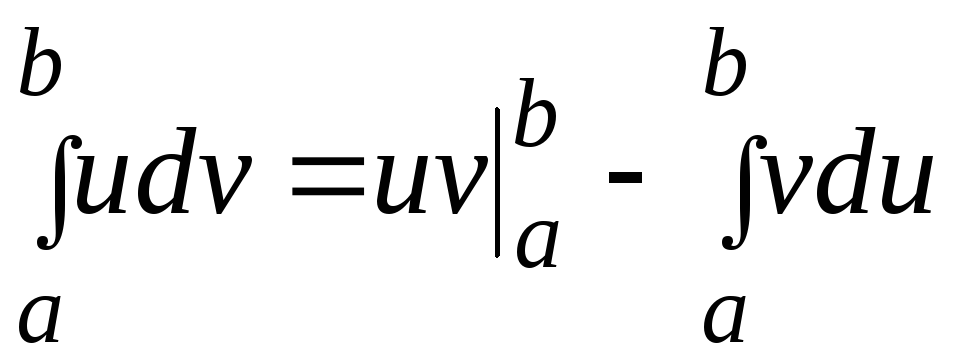
где
![]()
![]() непрерывно
дифференцируемые функции на отрезке
непрерывно
дифференцируемые функции на отрезке![]() .
.
Примеры. Вычислить интегралы.
1.
![]()
2.


12. Вычисление площадей плоских фигур
Из геометрического
смысла определенного интеграла следует,
что площадь криволинейной трапеции,
ограниченной непрерывной кривой
![]()
![]() двумя прямыми
двумя прямыми![]()
![]() и отрезком
и отрезком![]() оси
оси![]() ,
вычисляется по формуле
,
вычисляется по формуле![]() (I)
(I)
Если фигура
ограничена непрерывными кривыми
![]() и
и![]() ,
,![]() для всех
для всех![]() ,
и прямыми
,
и прямыми![]() и
и![]() то её площадь равна
то её площадь равна![]() (II)
(II)
Если фигура
заключена между кривыми
![]() и
и![]() ,
,![]() то находим абсциссы точек пересечения
данных кривых и вычисляем площадь фигуры
по формуле (II).
то находим абсциссы точек пересечения
данных кривых и вычисляем площадь фигуры
по формуле (II).
 Пример.
Найти площадь фигуры, ограниченной
параболами
Пример.
Найти площадь фигуры, ограниченной
параболами
![]() и
и![]() .
.
Решение.
Найдём абсциссы точек пересечения
данных кривых:
![]() .
По формуле (II):
.
По формуле (II):
![]()
