2.2. Распределенность терминов в суждении.

При проверке правильности умозаключений, построенных из простых категорических суждений, важно учитывать, во всем ли объеме берется термин в данном суждении или не во всем. Исходя из этого, можно говорить о распределенности, либо о нераспределенности термина в суждении.

Термин считается распределенным, если его объем полностью входит в объем другого термина или полностью исключается из него, т.е. в суждении идет речь о всех предметах, охватываемых этим термином. Другими словами, термин рассматривается в данном суждении во всем объеме.

Термин не распределен, если его объем частично входит в объем другого термина или частично исключается из него, т.е. в суждении говорится не о всех (а лишь о некоторых) предметах, охватываемых этим термином. Можно еще сказать, что в таком случае термин не рассматривается во всем объеме. При установлении распределенности терминов суждения удобно использовать круговые схемы, показывающие соотношение объемов субъекта и предиката.

Заштрихованная поверхность на этих схемах соответствует классу предметов, к которым непосредственно относится утверждение. Рассмотрим общеутвердительное суждение:«Все металлы электропроводны».S- понятие «металлы», Р - понятие «электропроводные материалы». Соотношение объемовSи Р передает следующая схема:

Р

S

В данном суждении речь идет о всех металлах, т.е. объем субъекта полностью включен в объем предиката. Следовательно субъект распределен. Что касается предиката, то понятие ’’электропроводной материал’’не рассматривается в суждении во всем объеме, т.е. лишь некоторые электропроводные материалы являются именно металлами. Объем предиката частично включен в объем субъекта, следовательно, предикат не распределен. Эту ситуацию можно интерпретировать еще и так: в данном суждении дается информация обо всем объеме субъекта и лишь о части объема предиката.

Теперь проанализируем еще один пример общеутвердительного суждения: ’’Все квадраты – равносторонние прямоугольники’’. Субъектом в данном случае является понятие’’квадрат’’, предикатом –’’равносторонний прямоугольник’’. Соотношение их объемов передает следующая схема:

В данном суждении речь идет о всех квадратах и обо всех равносторонних прямоугольниках, следовательно, и Sи Р являются распределенными.

2. Возьмем пример частноутвердительного суждения (I):’’Некоторые студенты проживают в общежитии’’.S–’’студент’’, Р –’’лицо, проживающее в общежитии’’.

S

P

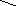
В данном суждении говорится лишь о части студентов и о части лиц, проживающих в общежитии, т.е. объемы терминов суждения частично совпадают. Это означает, что оба термина не распределены.

Рассмотрим еще одно частноутвердительное суждение: ’’Некоторые врачи – хирурги’’. Отношение объемовSи Р в этом примере соответствуют следующей схеме:

S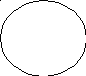

P

Объем субъекта в этом примере лишь частично входит в объем предиката, т.е. речь идет только о некоторой части врачей. А вот предикат взят в полном объеме, ибо все хирурги являются врачами. Таким образом, Sне распределен, а предикат – распределен.

3. Общеотрицательное суждение (Е). Пример: ’’Ни одна картина этого мастера не сохранилась до наших дней’’.S–’’картина этого мастера’’, Р –’’картина, которая сохранилась до наших дней’’. Объемы терминов суждения находятся в отношении внеположности:

S Р

Объемы терминов суждения в данном случае полностью исключают друг друга, т.е. не имеют общих элементов. Речь идет обо всем множестве S и обо всем множестве Р (Ни одна картина, сохранившаяся до наших дней, не принадлежит данному мастеру). Это позволяет сделать вывод, что оба термина в общеотрицательных суждениях распределены.

4. Частноотрицательное суждение (О). В высказываниях этого вида говорится, что часть множества S не включается в множество Р. Например:’’Некоторые студенты не проживают в общежитии’’. Отношения между объемамиSи Р передает следующая схема:

S Р

Субъект («студент») не распределен, т. к. речь идет лишь о части студентов. Предикат же («лицо проживающее в общежитии») распределен, ибо в нем мыслятся все лица проживающие в общежитии, ни одно из которых не включено в ту часть студентов о которой ид5ет речь в данном суждении.

Распределенность терминов в суждениях А, У, Е, О отражена в следующей таблице где знак ’’+’’означает, что термин распределен, а знак’’–’’– не распределен.

Термин	Вид суждения
	А	I	Е	О
S	+	–	+	–
Р	– (+)	– (+)	+	+