
2.9.Определенный интеграл
Определенный интеграл. Условия интегрируемости функций. Формула Ньютона- Лейбница. Основные свойства определенного интеграла. Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла.
Применение определенного интеграла в экономике. Применение определенного интеграла для вычисления площадей фигур, длин дуг плоских кривых и объемов тел. Приближенные методы вычисления определенных интегралов. Несобственные интегралы.
2.10. Кратные интегралы
Определение двойного интеграла. Геометрический смысл двойного интеграла. Сведение двойного интеграла к повторному. Тройной интеграл. Приложения кратных интегралов.
2.11.Обыкновенные дифференциальные уравнения
Основные понятия теории обыкновенных дифференциальных уравнений. Задача Коши. Теорема существования и единственности решения. Составление дифференциального уравнения первого порядка. Модели экономической динамики.
Дифференциальные уравнения первого порядка. Методы интегрирования дифференциальных уравнений первого порядка. Линейные дифференциальные уравнения первого порядка.
Линейные дифференциальные уравнения высших порядков. Однородные и неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью. Метод Лагранжа вариации произвольной постоянной. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
2.12.Ряды
Понятие числового ряда. Сходимость числового ряда. Простейшие свойства сходящихся рядов. Необходимое условие сходимости числового ряда. Признаки сходимости рядов с положительными членами. Знакопеременные ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
Функциональные ряды. Степенные ряды. Теорема Абеля. Область и интервал сходимости степенного ряда. Ряды Тейлора и Маклорена. Разложение элементарных функций в степенные ряды. Применение рядов к приближенным вычислениям.
Ряды Фурье. Разложение функций в ряды Фурье.
Примерный перечень вопросов
по дисциплине «Высшая математика (1 часть)»
Матрицей размера
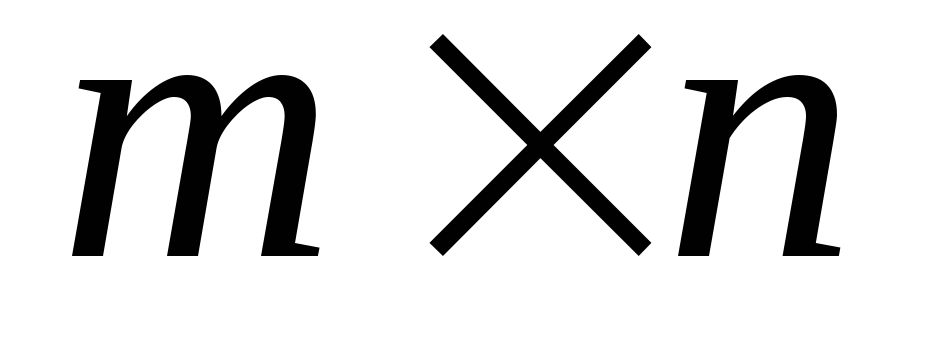 называется ….
называется ….Единичной матрицей второго порядка является матрица….
Нулевая матрица может быть
Транспонированная матрица к матрице
 содержит всегда
содержит всегдаМатрицы
 и
и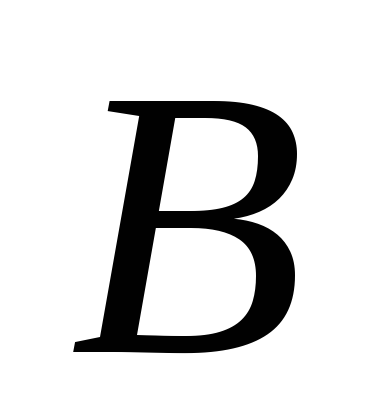 можно складывать, если только
можно складывать, если толькоУмножить матрицу на число
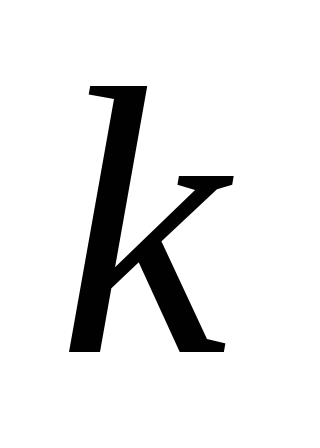 означает
означаетМатрицы
 и
и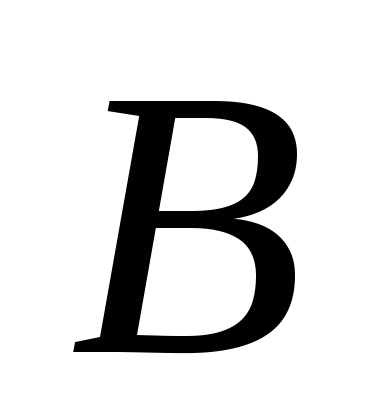 называются согласованными, если только
называются согласованными, если толькоМатрицы
 и
и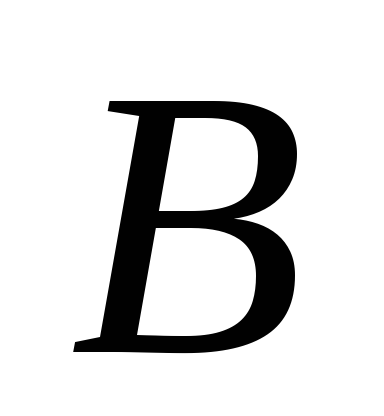 можно перемножать, если только они
можно перемножать, если только ониПри умножении матриц
 и
и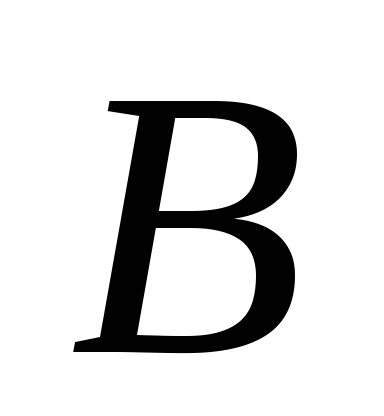 всегда получают
всегда получаютКакая из формул является неверной для умножения матриц:
Матрица
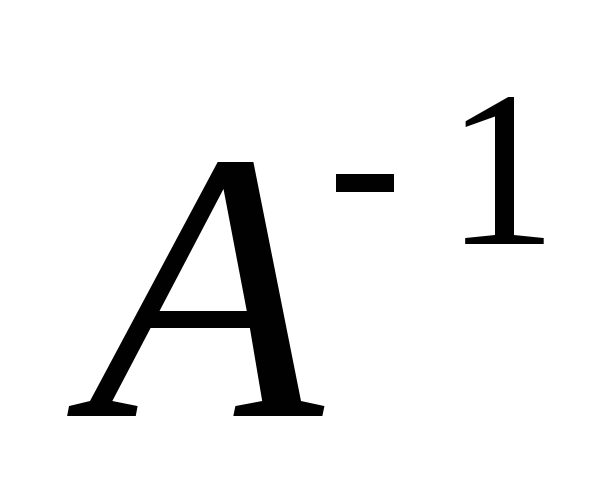 называется обратной к матрице
называется обратной к матрице ,
если:
,
если:Обратная матрица для матрицы
 вычисляется, только если
вычисляется, только еслиМатрица
 называется невырожденной,
называется невырожденной,Обратная матрица к матрице
 вычисляется по формуле:
вычисляется по формуле:Какое равенство неверно для обратных матриц:
Определитель матрицы вычисляется, только если матрица

Определитель второго порядка вычисляется по формуле:
Определитель квадратной матрицы
 — это
— этоЕсли элементы строк или столбцов определителя пропорциональны, то определитель равен
При замене всех строк определителя соответствующими столбцами определитель
Определитель
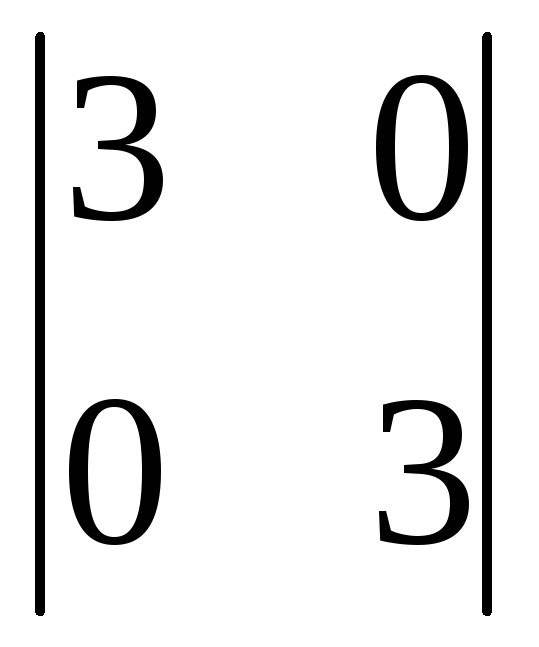 равен
равенМетод Гаусса (метод исключения неизвестных) позволяет найти
Однородная система линейных алгебраических уравнений
Система линейных алгебраических уравнений совместна, если
Величина, которая определяется только числовым значением, называется:
На плоскости вектор изображается
Единичным вектором называется вектор, имеющий
Векторы называются коллинеарными, если
Векторы называются компланарными, если
Линейными операциями над векторами называются
Сумму двух векторов на плоскости можно найти по
Вектор
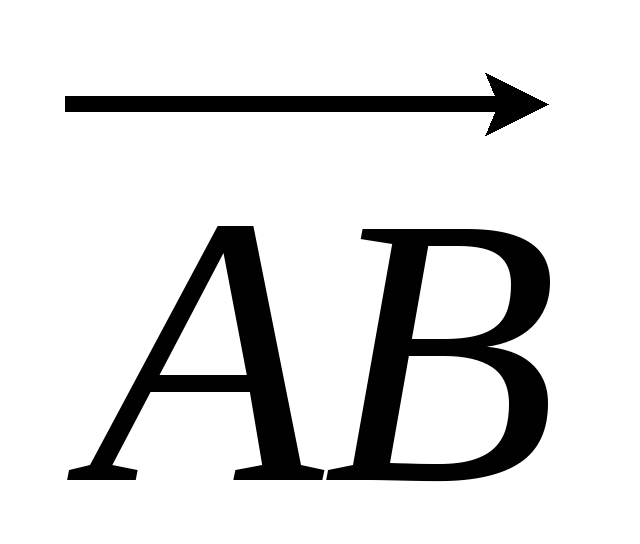 задан координатами точек
задан координатами точек и
и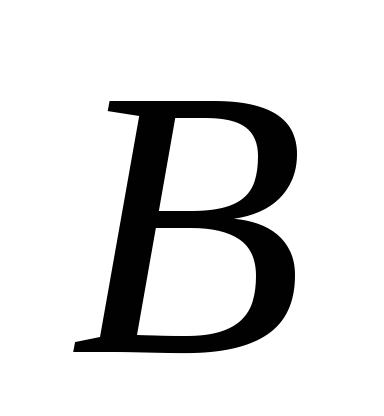 .
Тогда, чтобы найти координаты вектора
.
Тогда, чтобы найти координаты вектора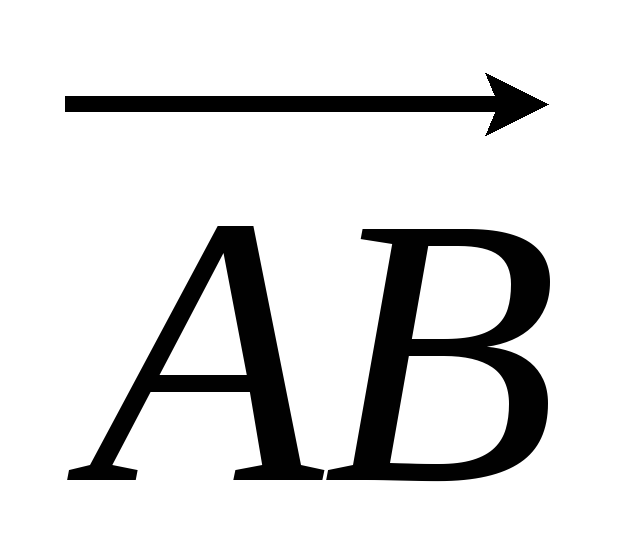 надо
надоУпорядоченная система трёх векторов называется базисом, если
Базис векторов называется ортонормированным, если
Скалярным произведением двух векторов
 и
и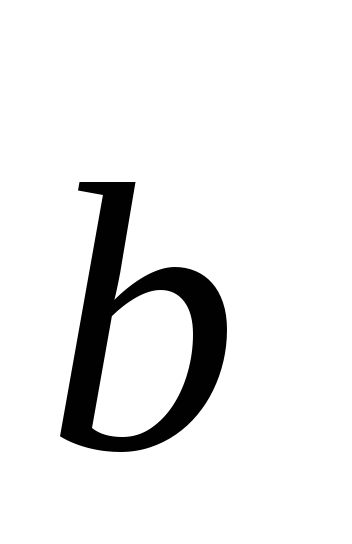 называются
называютсяСкалярный квадрат вектора равен
Если векторы
 и
и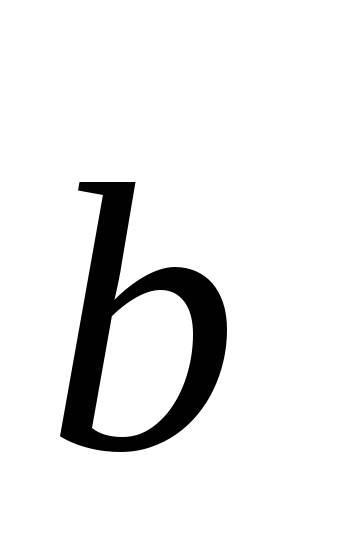 перпендикулярны, то их скалярное
произведение равно
перпендикулярны, то их скалярное
произведение равноЕсли скалярное произведение двух векторов равно 0, то вектора
Длина вектора
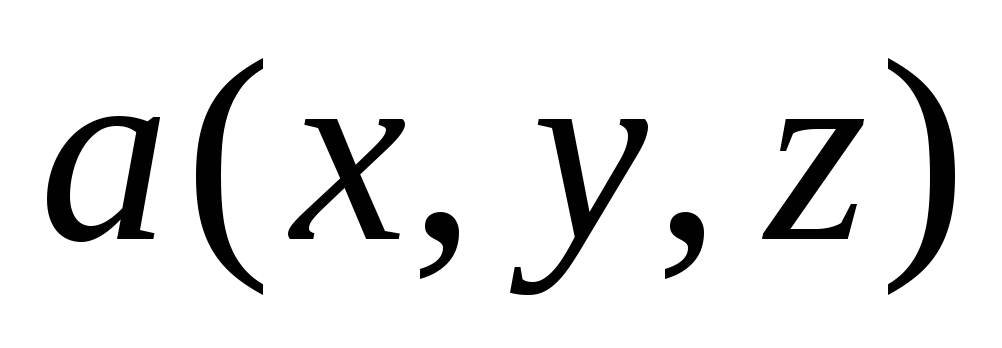 вычисляется по формуле
вычисляется по формулеДаны векторы
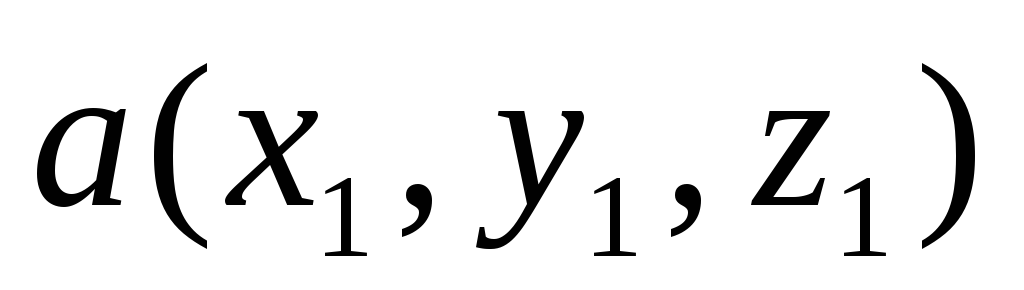 ,
,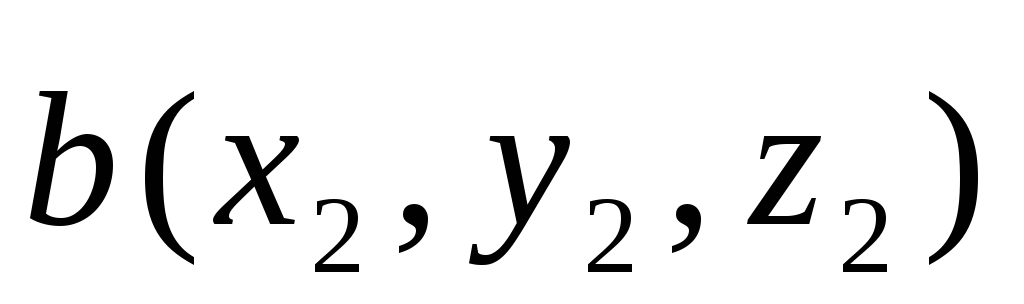 .
Тогда их скалярное произведение
вычисляется по формуле
.
Тогда их скалярное произведение
вычисляется по формулеВекторным произведением двух векторов называется
Векторное произведение векторов
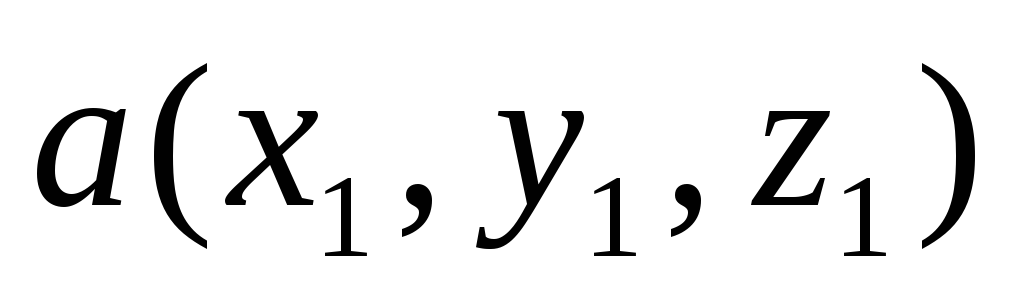 и
и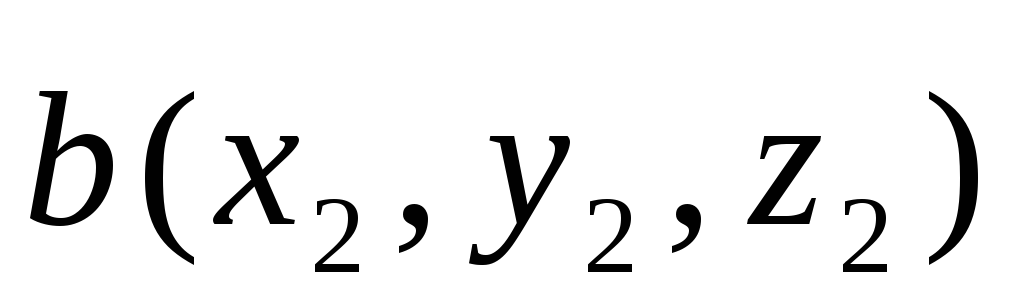 вычисляется по формуле
вычисляется по формулеЕсли смешанное произведение векторов,
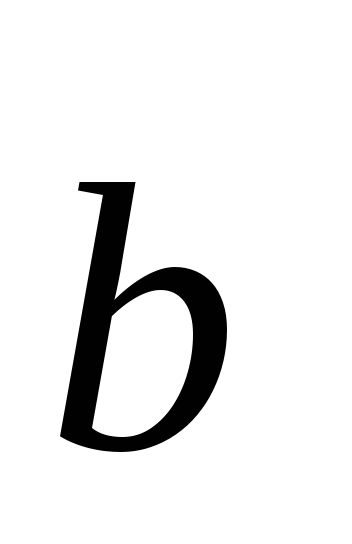 и
и ,
равно 0, то они
,
равно 0, то ониСмешанное произведение векторов
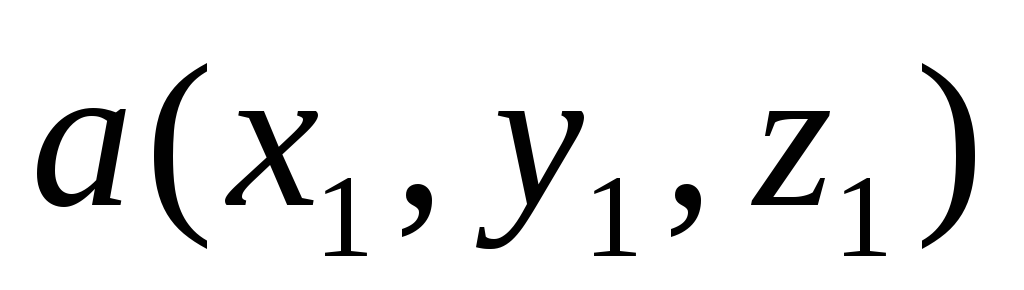 ,
,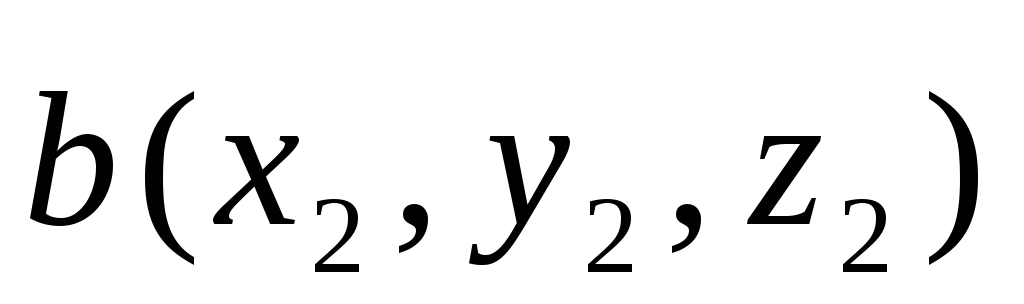 ,
,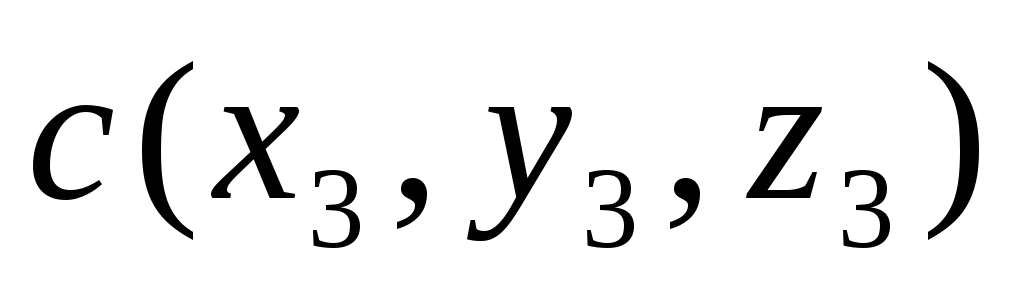 вычисляется по формуле
вычисляется по формулеУравнение прямой на плоскости, заданной точкой и нормальным вектором имеет вид:
Общее уравнение прямой на плоскости имеет вид
Уравнение прямой с угловым коэффициентом имеет вид
Каноническое уравнение прямой на плоскости имеет вид
Уравнение прямой на плоскости, проходящей через две точки, имеет вид
Числа
 и
и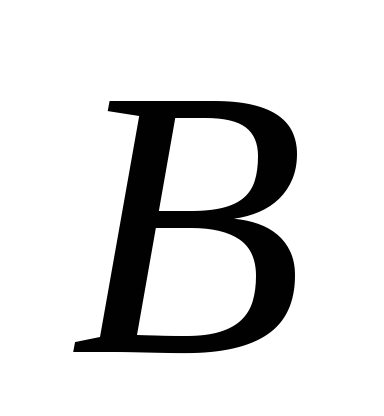 в уравнении прямой
в уравнении прямой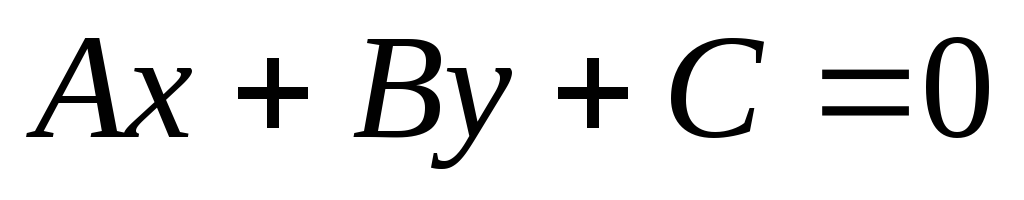 это
этоЧисла
 и
и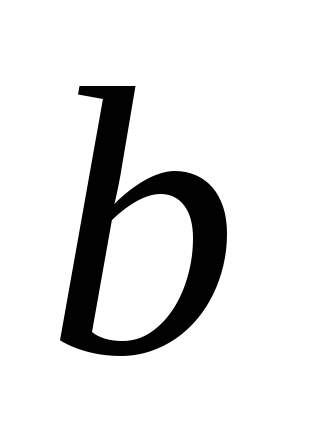 ,
взятые по модулю, в уравнении прямой
,
взятые по модулю, в уравнении прямой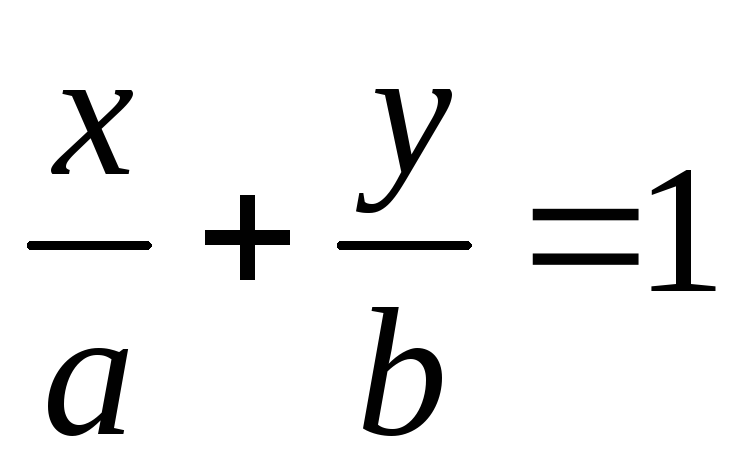 ,
это
,
этоЧисла
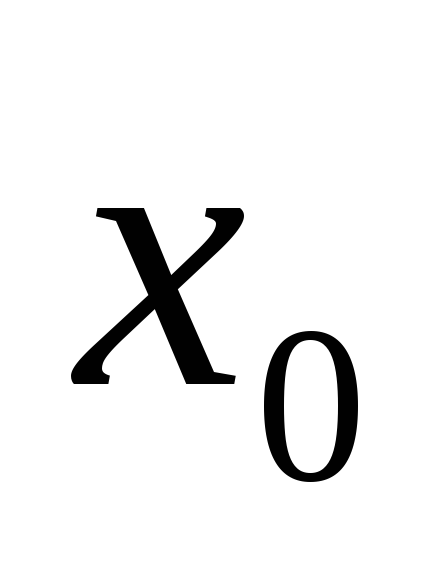 ,
,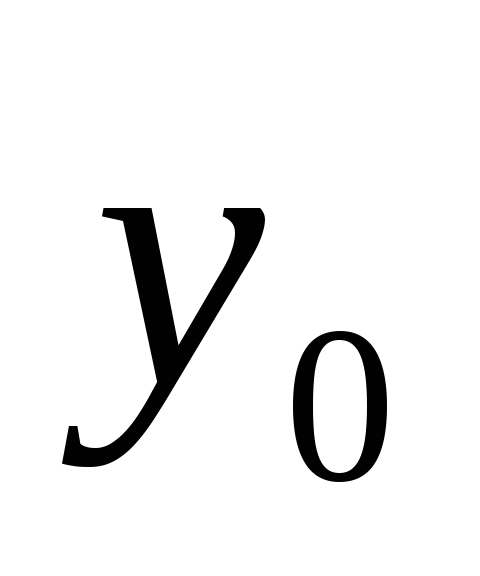 в уравнении прямой
в уравнении прямой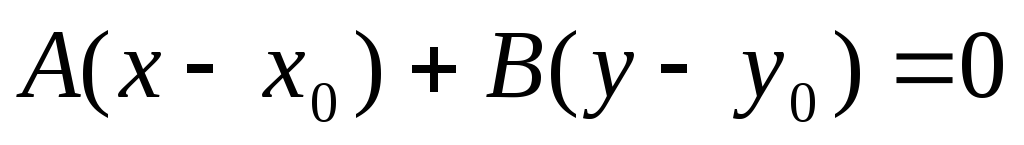 ,
это
,
этоПрямая
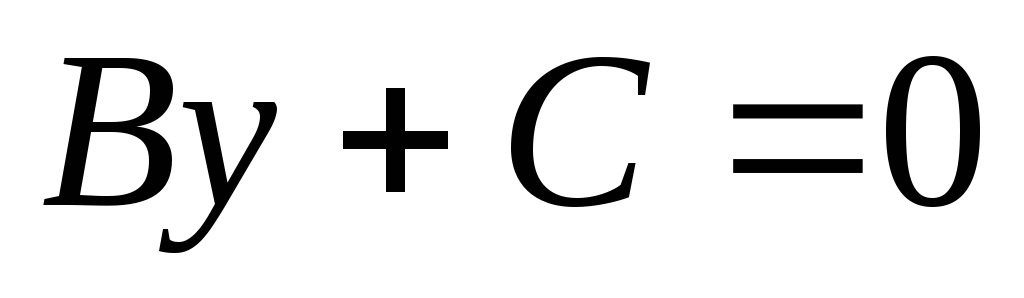 ,
,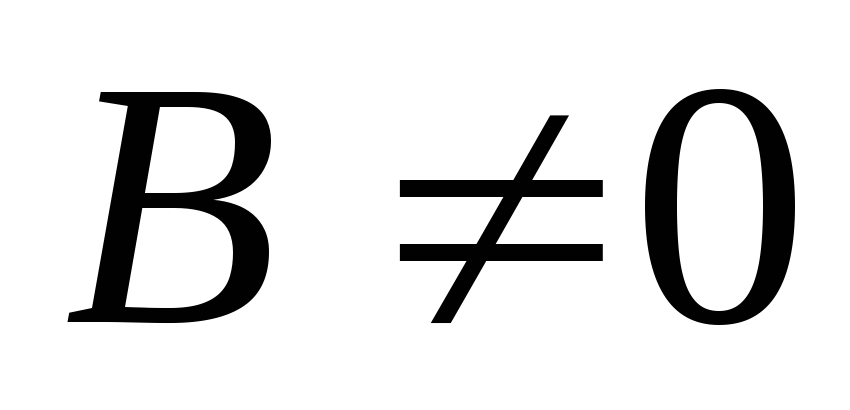 ,
,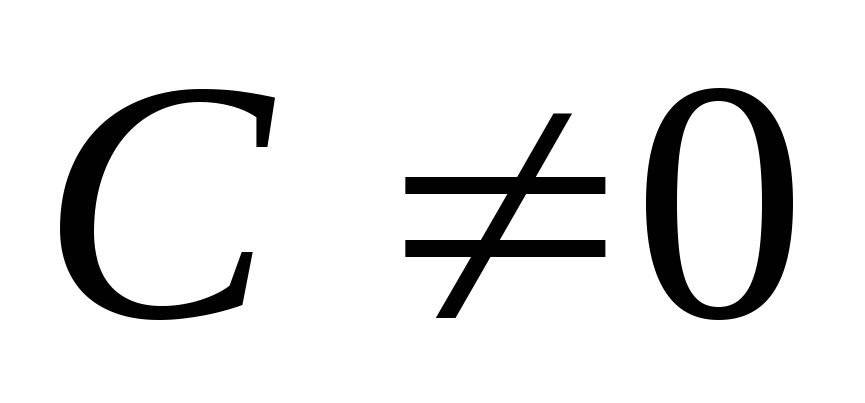 проходит
проходитПрямые
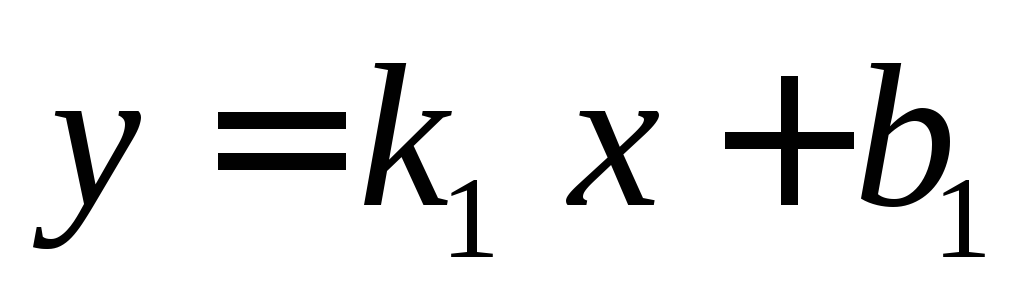 ,
,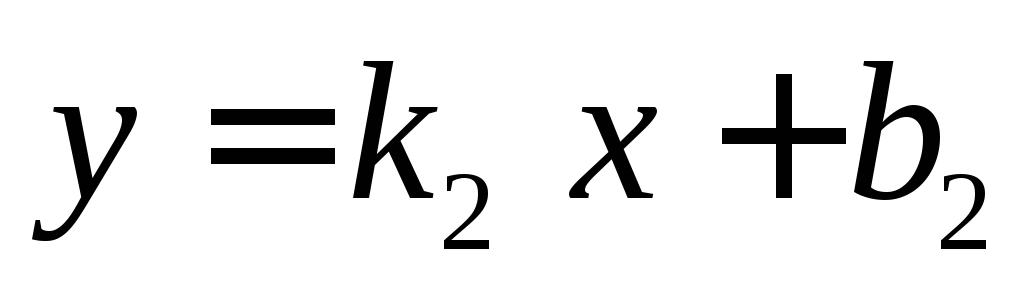 параллельны, если
параллельны, еслиУравнение плоскости, заданной точкой и нормальным вектором, имеет вид
Числа
 ,
,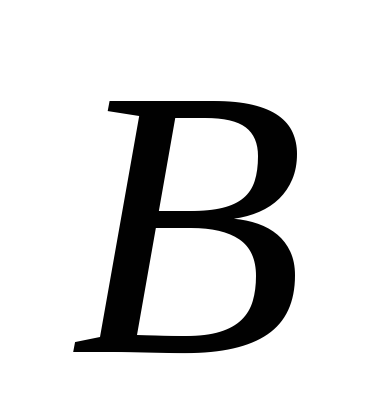 ,
, в уравнении плоскости
в уравнении плоскости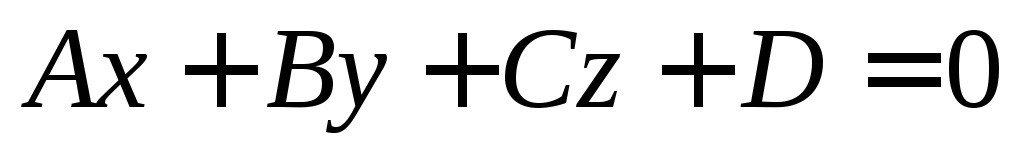 это
этоОбластью определения функции
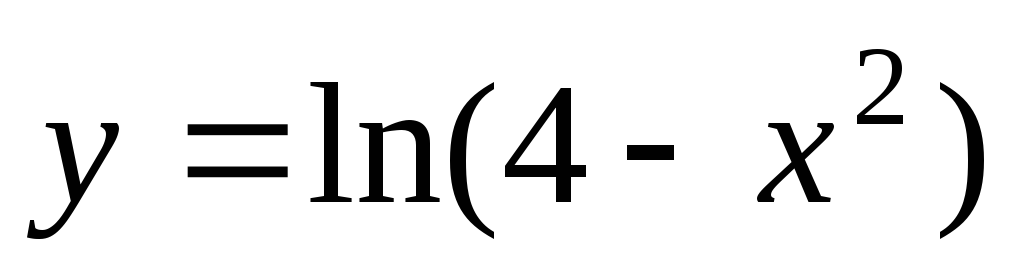 является
промежуток:
является
промежуток:Какая из приведенных функций не является элементарной:
Какая из приведенных функций является ограниченной:
Бесконечно малой последовательностью называется последовательность, имеющая предел, равный:
Последовательность называется сходящейся, если она:
Пятый член последовательности
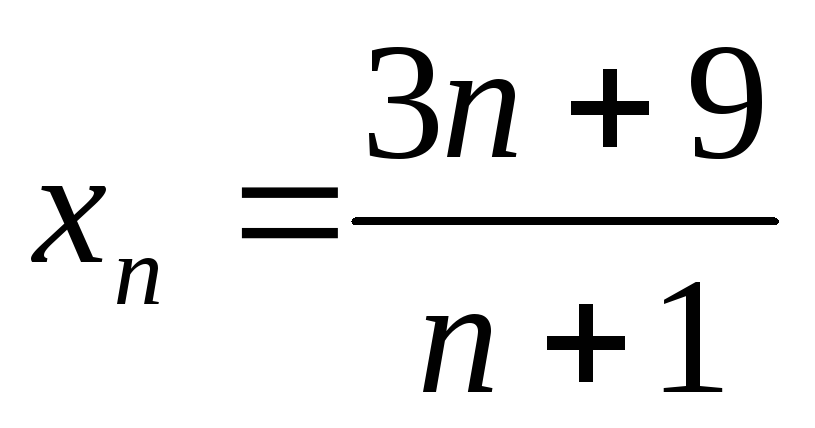 равен:
равен:Функция
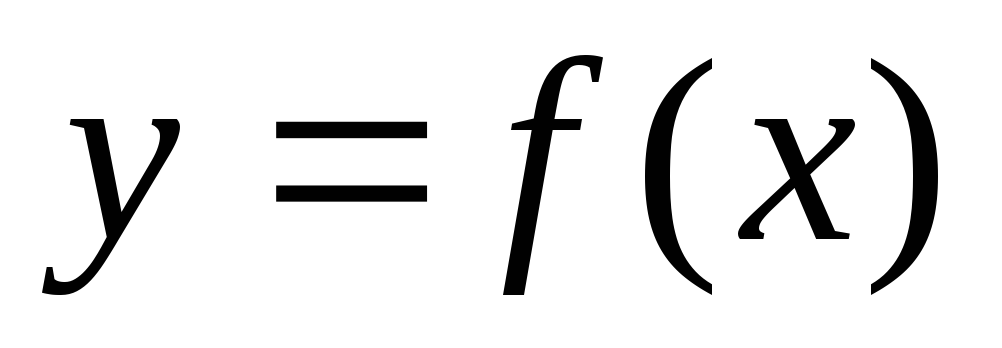 называется
бесконечно большой функцией при
называется
бесконечно большой функцией при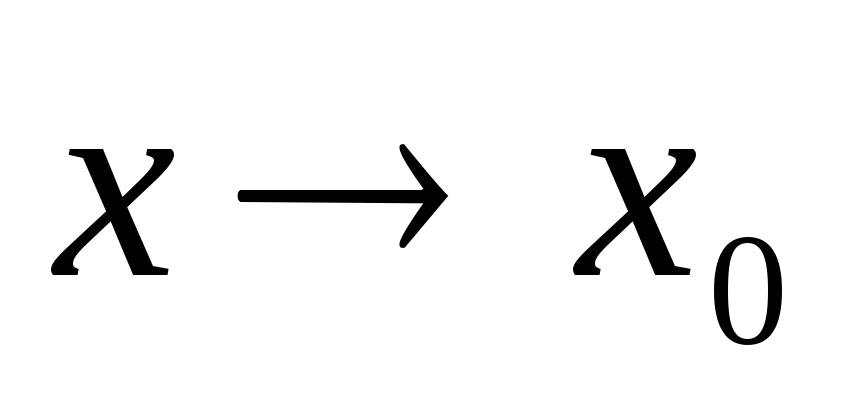 ,
если:
,
если:Числом е называется предел:
Предел
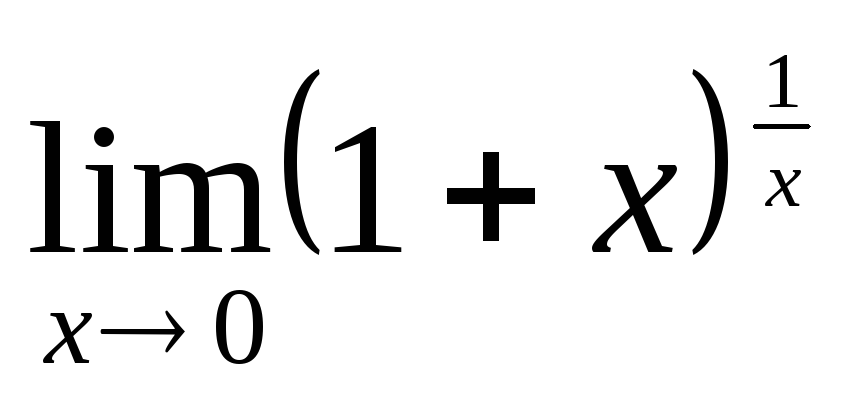 равен:
равен:Производная постоянной равна:
Производная функции
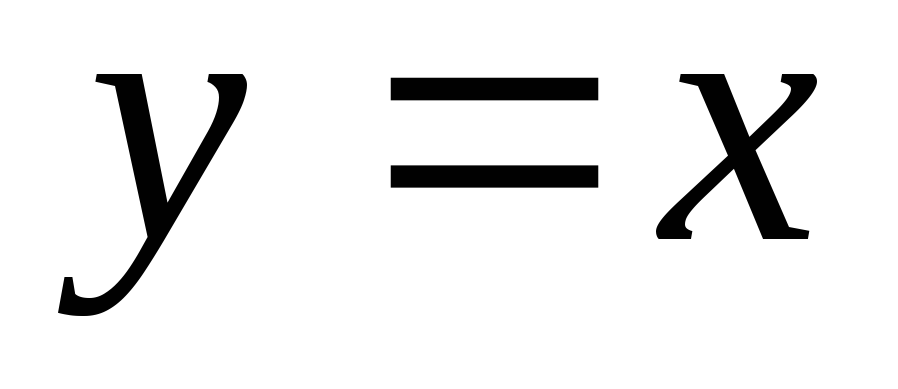 равна:
равна:Производная частного двух дифференцируемых функций
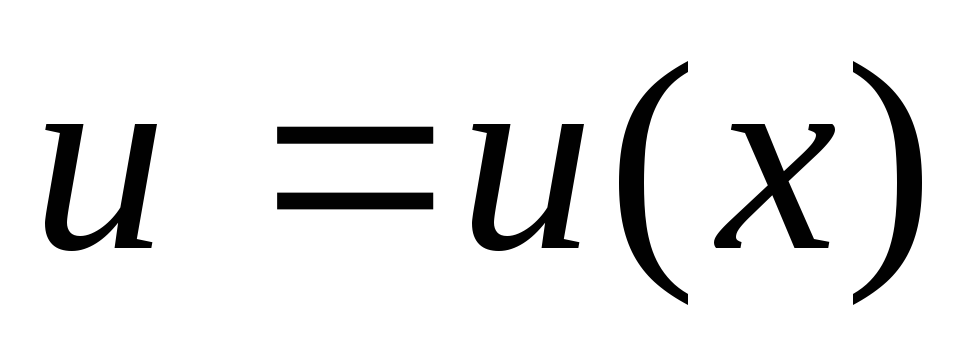 и
и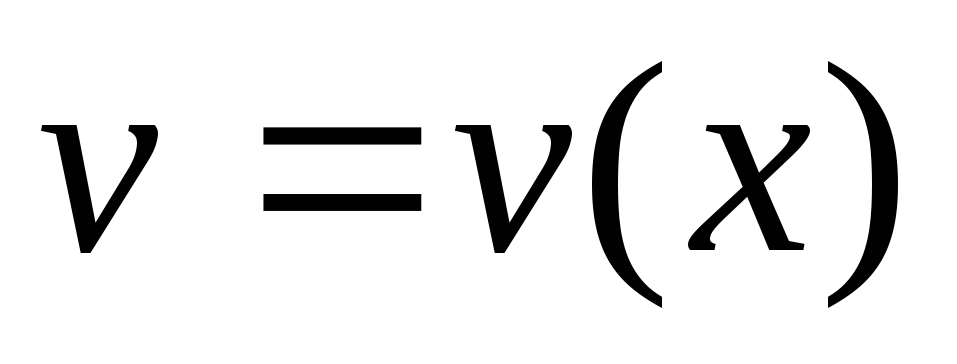 определяется по формуле:
определяется по формуле:Правило Лопиталя состоит в следующем: если
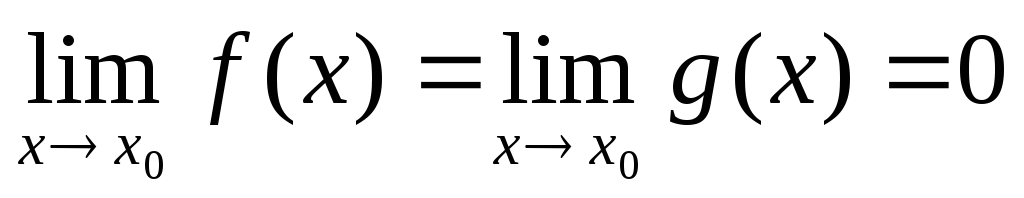 или
или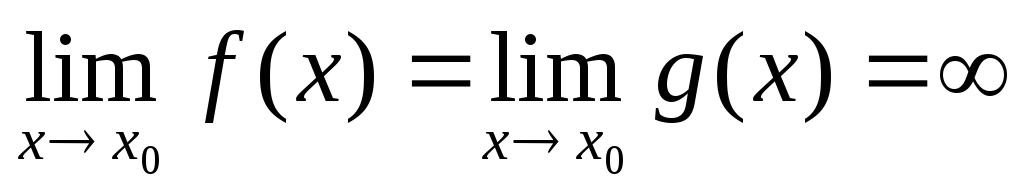 ,
то:
,
то:Операция нахождения производной функции
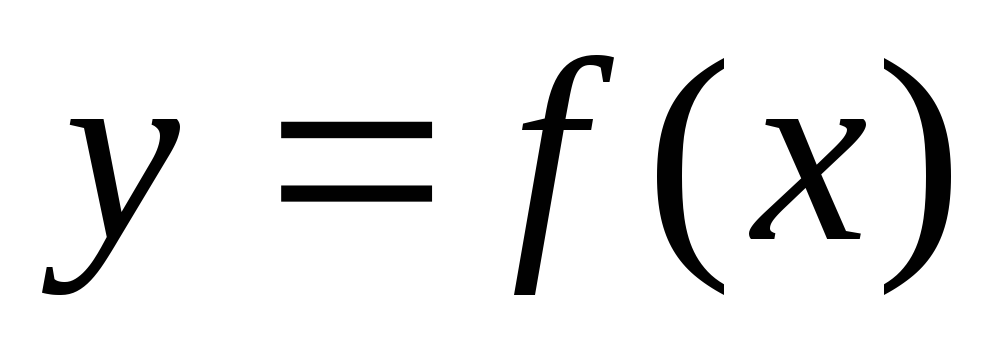 называется:
называется:Если функция
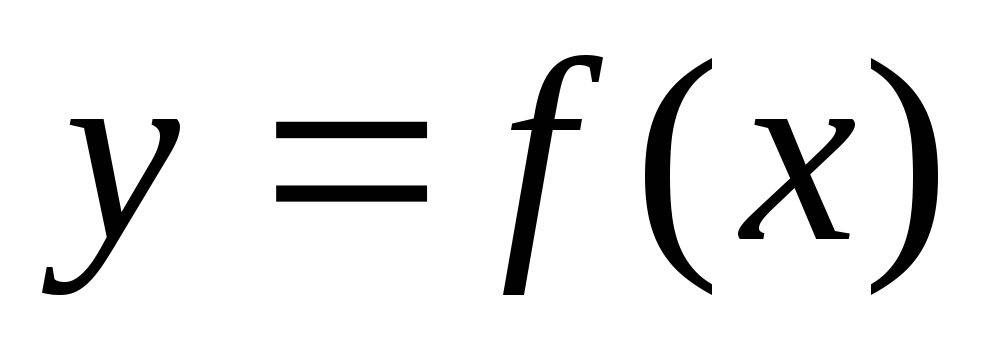 дифференцируема на
дифференцируема на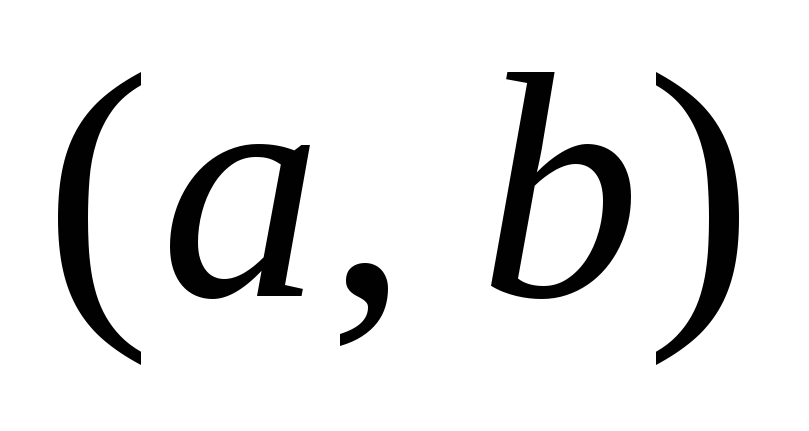 и
и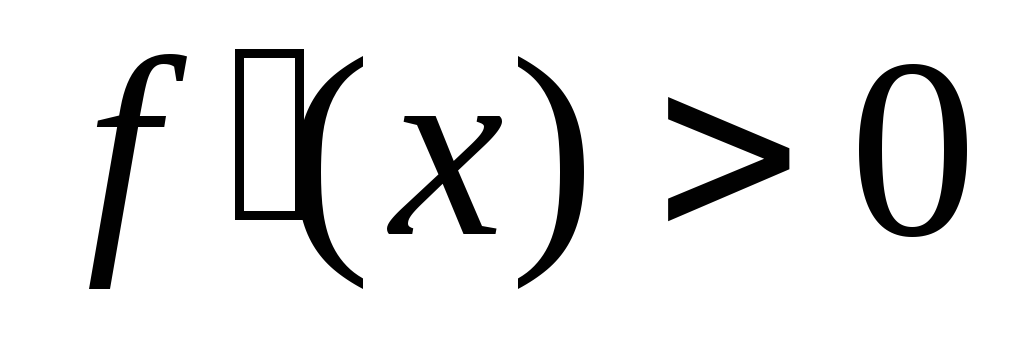 для любого
для любого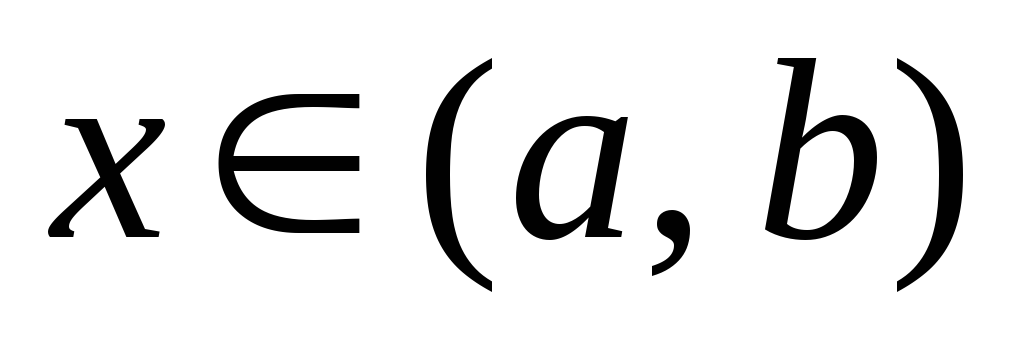 ,
то на этом интервале функция:
,
то на этом интервале функция:Если при переходе через критическую точку
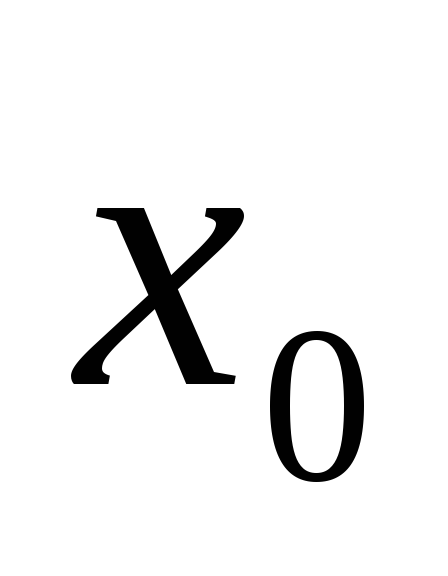 производная
производная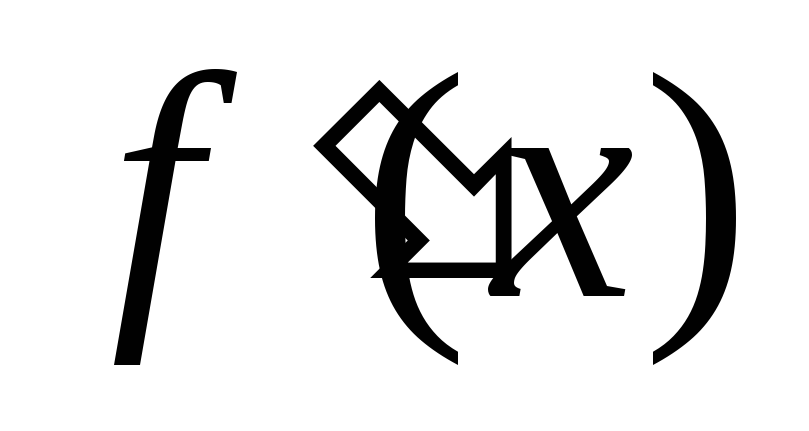 меняет знак с “+” на “–“, то
меняет знак с “+” на “–“, то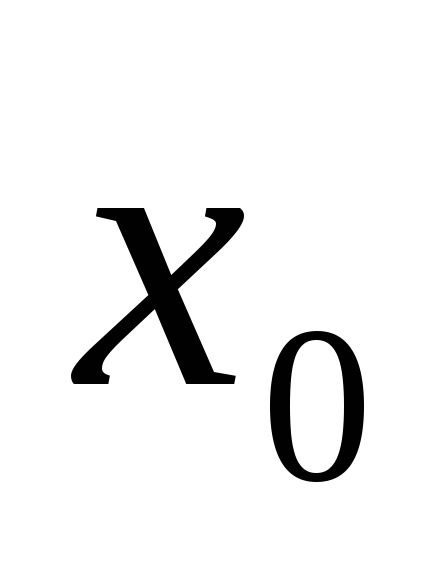 есть:
есть:
Основная литература
Яблонский А.И., Кузнецов А.В., Шилкина Е.И. и др.; под общ.ред. Самаля С.А. Высшая математика: Общий курс. Учебник – 2-е изд., переработ. Мн.: Выш. шк., 2000.- 351 с.
Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов: Учебник для вузов / Под ред. Н.Ш.Кремера −2-е изд., переработ. и доп. М.: ЮНИТИ, 2001.-471 с.
Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. – М.: Рольф, 2001. – 576 с.
Ермаков В.И., Бобрик Г.И. и др. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И. Ермакова. – М.: ИНФРА – А, 2002. – 575 с.
