ТЕСТЫ ТВиМС с ответами
.docТЕСТЫ
по курсу «Теория вероятностей и математическая статистика»
-
Вероятность события
 это:
это:
-
отношение
 где
где
 число
исходов испытаний, благоприятствующих
появлению события
число
исходов испытаний, благоприятствующих
появлению события
 ,
,
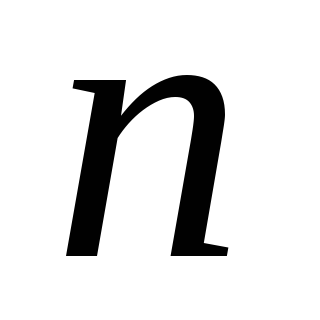 -общее
число исходов испытаний;
-общее
число исходов испытаний; -
числовая функция, определенная на поле событий
 и
удовлетворяющая трем условиям:
и
удовлетворяющая трем условиям:
-
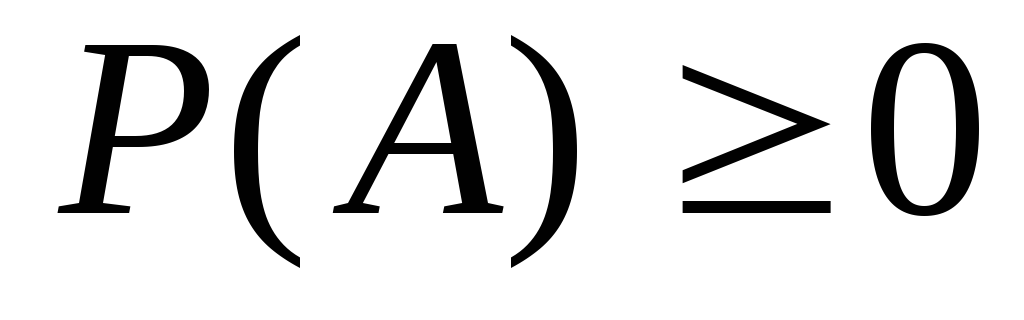 ; 2.
; 2.
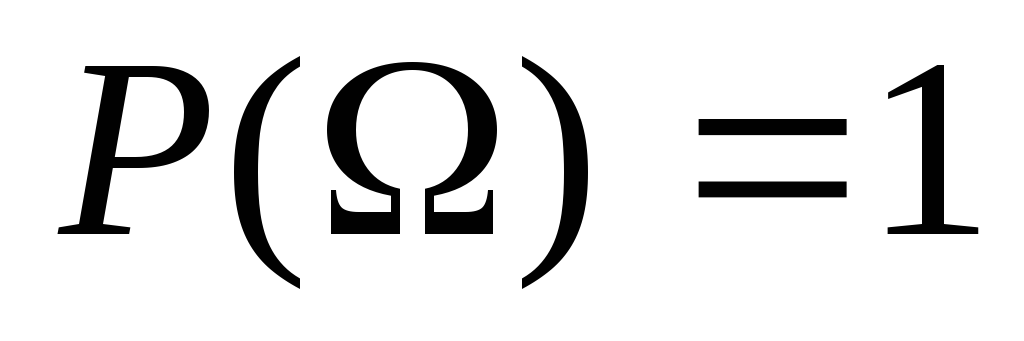 ;
3.
;
3.

-
числовая мера появления события
 в
в
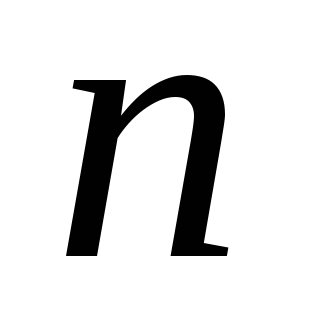 испытаниях;
испытаниях; -
отношение
 где
где
 число
появлений событий А в
число
появлений событий А в
 испытаниях;
испытаниях; -
число элементарных событий в некотором подмножестве
 .
.
2. Какие способы задания вероятностей вы знаете:
-
классический, динамический, точечный, геометрический;
-
статистический, геометрический, биноминальный, классический;
-
геометрический, классический, дискретный, статистический;
-
классический, геометрический, точечный, статистический;
-
классический, геометрический, статистический, комбинаторный.
3. Когда применяется классический способ задания вероятности:
-
пространство элементарных событий бесконечно, все события равновозможные и независимые;
-
пространство элементарных событий замкнуто, все события независимы;
-
пространство элементарных событий конечно, все события равновозможные;
-
пространство элементарных событий конечно, все элементарные события независимы.
4. Когда применяется геометрический способ задания вероятности:
-
пространство элементарных событий бесконечно, все события равновозможные и независимые;
-
пространство элементарных событий замкнуто, все события независимы;
-
пространство элементарных событий конечно, все события равновозможные;
-
пространство элементарных событий конечно, все элементарные события независимы.
5. Назовите основные аксиомы вероятностей:
-
 ;
;
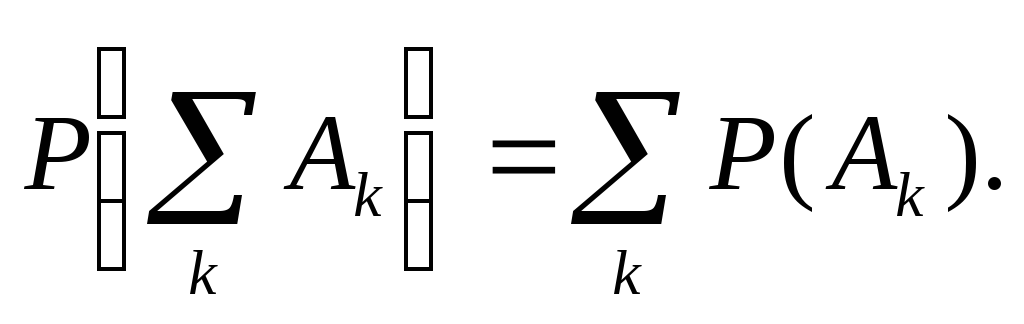 ;
; ;
; -
 ;
;
 ;
; ;
; -
 ;
; ;
;
-
 ;
; ;
;
 .
.
6. Суммой двух событий
![]() и
и
![]() называют:
называют:
-
событие
 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию
 или
или
 ;
; -
событие
 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию
 или
или
 ;
; -
событие
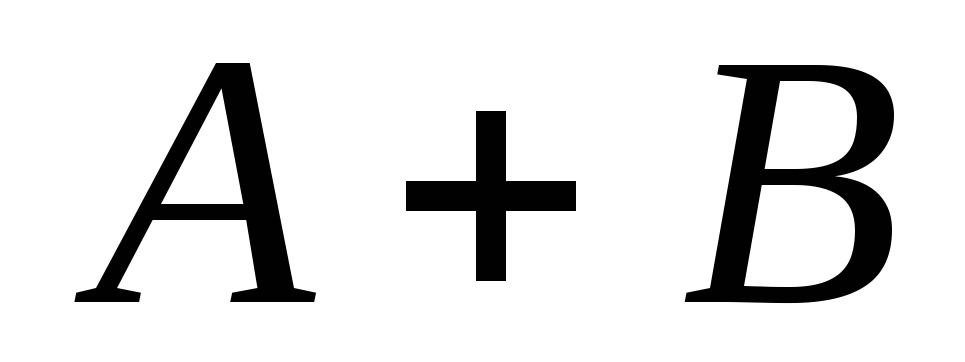 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию
 и
и
 ;
; -
событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию
 и
и
 ;
; -
событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию
 и
и
 ;
;
7.
Произведением двух событий
![]() и
и
![]() называют:
называют:
-
событие
 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию
 или
или
 ;
; -
событие
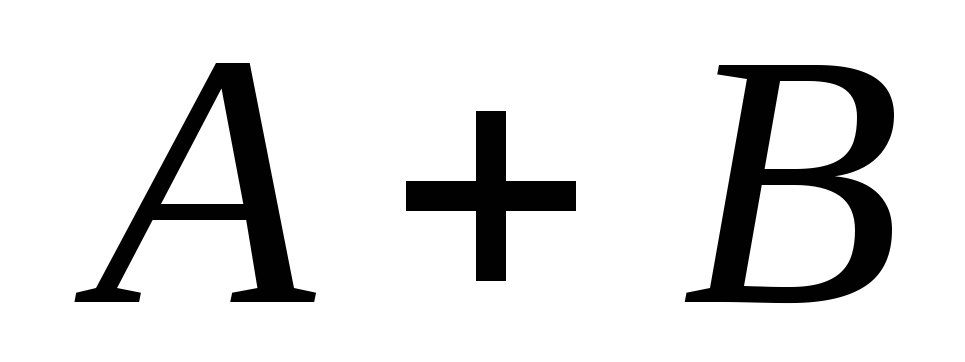 ,
состоящее из элементарных событий,
принадлежащих или событию
,
состоящее из элементарных событий,
принадлежащих или событию
 или
или
 ;
; -
событие
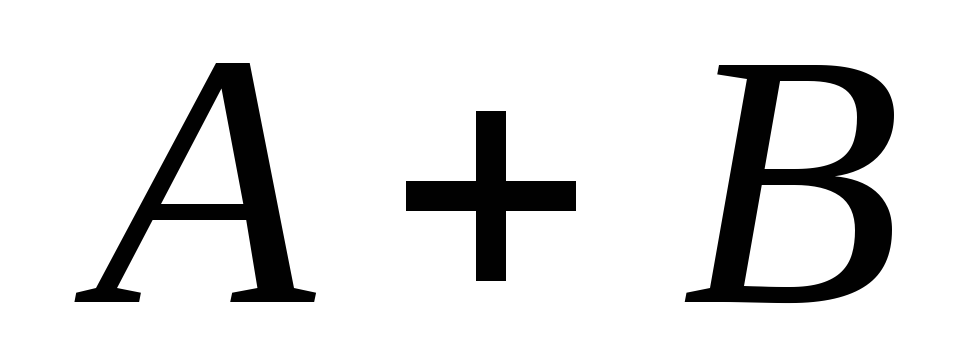 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию
 и
и
 ;
; -
событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию
 и
и
 ;
; -
событие
 ,
состоящее из элементарных событий,
принадлежащих и событию
,
состоящее из элементарных событий,
принадлежащих и событию
 и
и
 ;
;
-
Вероятность суммы двух совместных событий
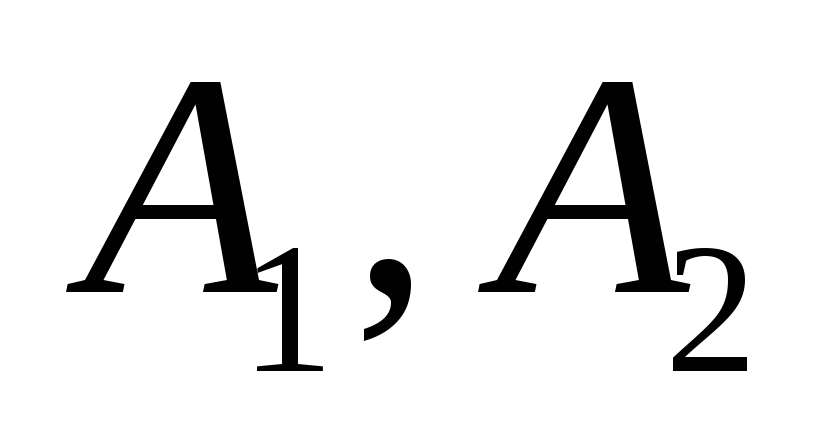 равна:
равна:
-
Вероятность произведения двух совместных событий рана:
-
Формула полной вероятности:
-
Законы распределения случайной дискретной величины представляются в виде:
-
функции распределения
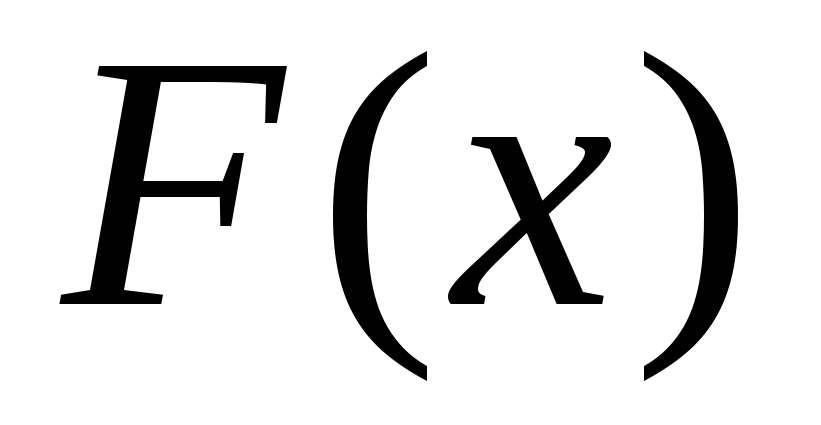 и совокупностью значений
и совокупностью значений
 ;
;
-
функции распределения
 и функции плотности распределения
и функции плотности распределения
 ;
; -
функции распределения
 и совокупностью значений
и совокупностью значений
 ;
; -
функции распределения
 и рядом распределения
и рядом распределения
 ;
; -
функции распределения
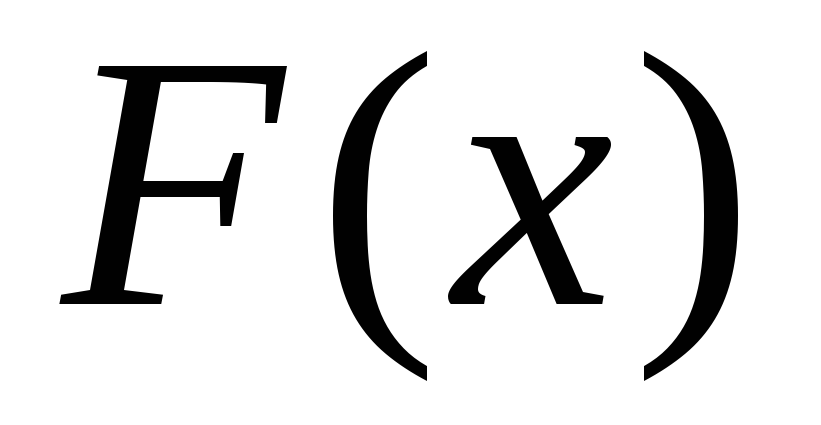 и
и
 ;
; -
функции распределения
 и
и
 .
.
-
Законы распределения непрерывной случайной величины представляются в виде:
-
функции распределения
 и совокупностью значений
и совокупностью значений
 ;
;
-
функции распределения
 и функции плотности распределения
и функции плотности распределения
 ;
; -
функции распределения
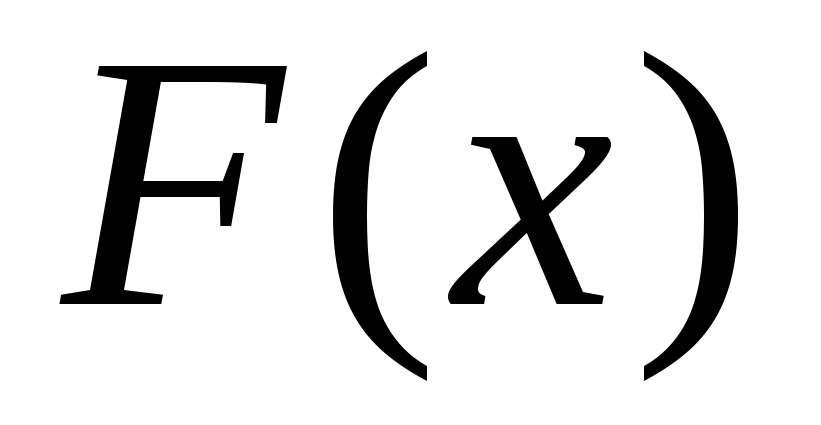 и совокупностью значений
и совокупностью значений
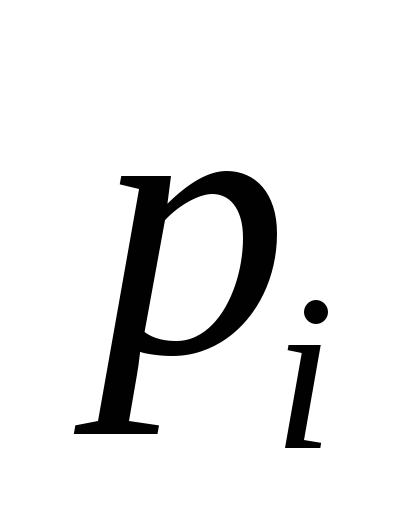 ;
; -
функции распределения
 и рядом распределения
и рядом распределения
 ;
; -
функции распределения
 и
и
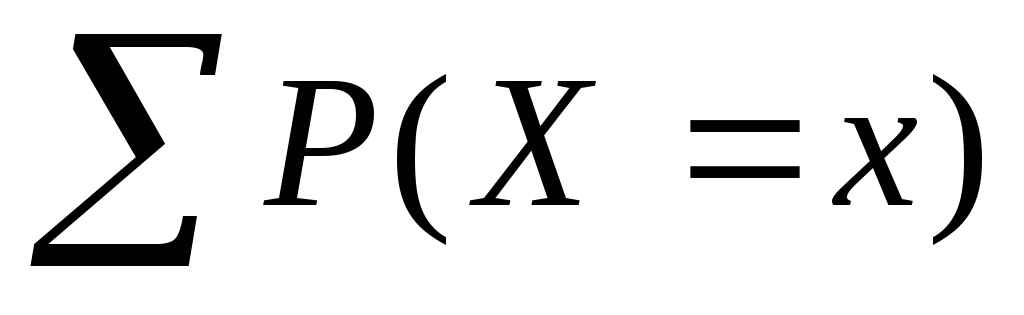 ;
; -
функции распределения
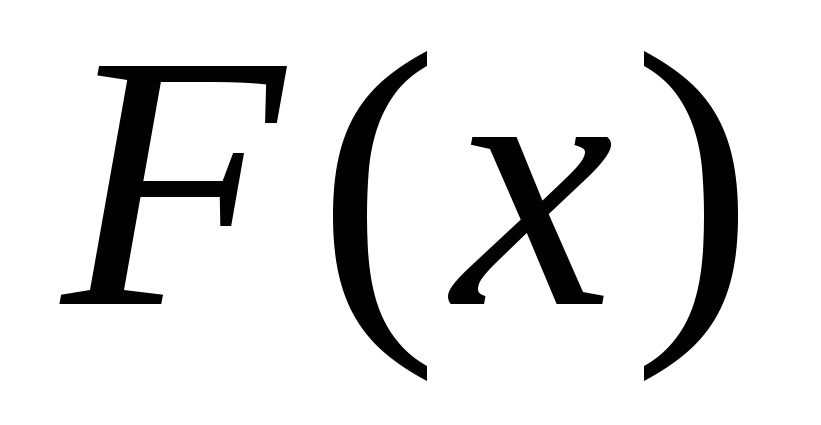 и
и
 .
.
-
Функция распределения случайной величины это:
-
Вероятность того, что

-
Вероятность того, что

-
Вероятность того, что

-
Вероятность того, что

-
Вероятность того, что
 .
.
-
Функция плотности распределения случайной величины
 это:
это:
-
средняя плотность распределения вероятности на интервале
 ,
равная
,
равная
 ;
; -
предельная средняя плотность вероятности на интервале
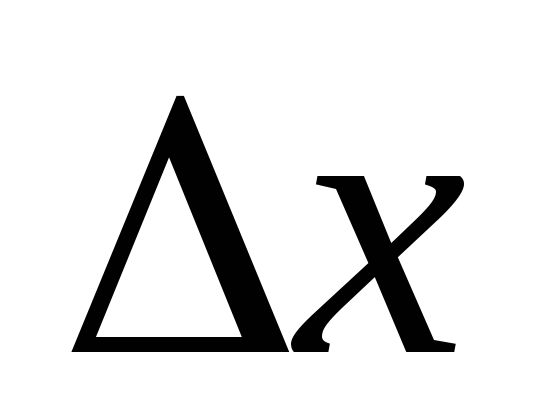 ,
равная
,
равная ;
; -
предельная средняя плотность вероятности на интервале
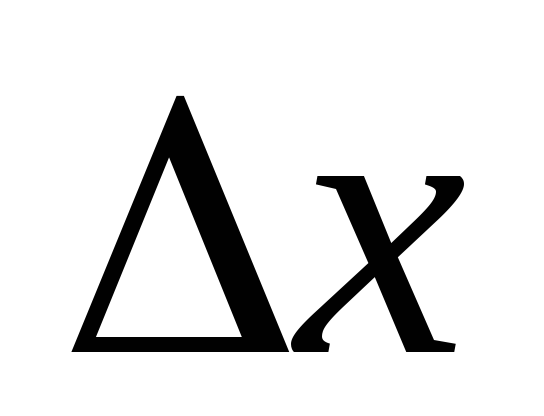 ,
равная
,
равная ;
; -
предельная средняя плотность вероятности на интервале
 ,
равная
,
равная ;
; -
средняя плотность распределения вероятности на интервале
 ,
равная
,
равная
 ;
;
-
Основные числовые характеристики дискретных случайных величин это:
-
Среднее арифметическое, дисперсия, квантиль, моменты
 -того
порядка, мода и медиана;
-того
порядка, мода и медиана; -
Дисперсия, центральные и начальные моменты
 -того
порядка, среднее геометрическое, мода
и медиана;
-того
порядка, среднее геометрическое, мода
и медиана; -
Математическое ожидание, мода, медиана, дисперсия, среднее квадратичное отклонение, центральные и начальные моменты
 -того
порядка.
-того
порядка. -
Математическое ожидание, среднее арифметическое, дисперсия, среднее квадратичное отклонение, мода, медиана, центральные и начальные моменты
 -того
порядка.
-того
порядка. -
Математическое ожидание, мода, медиана, дисперсия, среднее квадратичное отклонение, центральные и начальные моменты
 -того
порядка, эксцесс, асимметрия.
-того
порядка, эксцесс, асимметрия.
-
Функция распределения
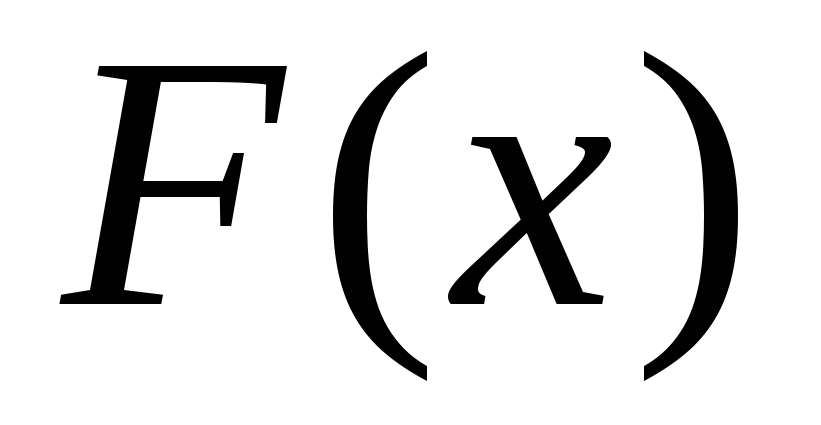 и
функция плотности распределения имеют
и
функция плотности распределения имеют
 следующие
свойства:
следующие
свойства:
-
Дисперсия случайно величины равна:
-
Математическое ожидание непрерывной случайной величины равно:
-

-

-

-

-

-
 .
.
-
Нормальный закон распределения имеет следующую функцию плотности распределения
 :
:
-
Для нормального закона распределения вероятность попадания случайной величины в интервал
 равен:
равен:
-
Сущность предельных теорем и закона больших чисел заключается:
-
В определении числовых характеристик случайных величин при большом числе наблюдаемых данных;
-
В поведении числовых характеристик и законов распределения наблюдаемых значений случайных величин;
-
В определении области применения нормального закона распределения случайных величин при сложении большого количества случайных величин;
-
В поведении числовых характеристик и законов распределения случайных величин при увеличении числа наблюдений и опытов.
-
В определении суммарных значений основных характеристик законов распределения.
-
Коэффициент корреляции случайных величин характеризует:
-
Степень независимости между случайными величинами;
-
Степень нелинейной зависимости между случайными величинами;
-
Степень линейной зависимости между случайными величинами;
-
Степень регрессии между случайными величинами;
-
Степень разброса двух величин относительно математического ожидания.
-
Степень отклонения двух величин от их математических ожиданий.
-
Марковским случайным процессом называют такие процессы, у которых:
-
Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса; -
Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса; -
Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса; -
Плотность совместного распределения произвольных
 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса; -
Плотность совместного распределения произвольных
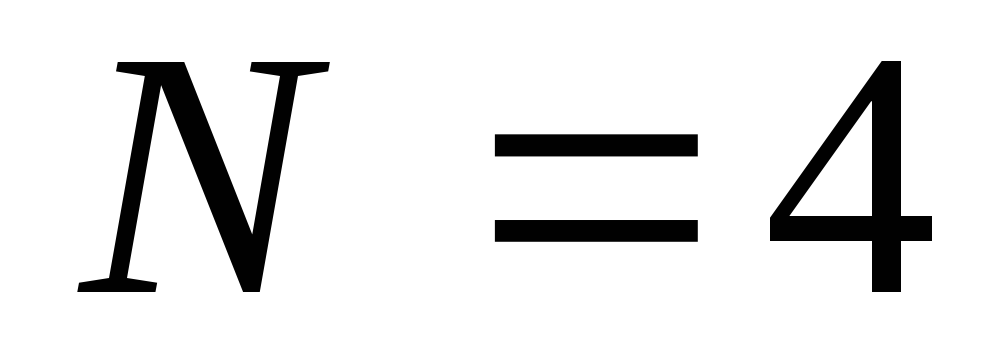 сечений полностью определяет поведение
процесса;
сечений полностью определяет поведение
процесса;
-
Марковскими цепями называю случайных процесс, у которого:
-
Сама функция подчиняется нормальному закону распределения;
-
Сама функция подчиняется показательному закону распределения;
-
Сама функция имеет дискретный характер;
-
Сама функция имеет непрерывный характер;
-
Сама функция подчиняется биноминальному закону распределения;
-
К оценкам генеральной совокупности предъявляются следующие требования:
-
Оценка должна быть стационарной, эргодичной и эффективной;
-
Оценка должна быть состоятельной, эргодичной и эффективной;
-
Оценка должна быть состоятельной, стационарной и эргодичной ;
-
Оценка должна быть состоятельной, эффективной и несмещенной;
-
Оценка должна быть несмещенной, стационарной и эффективной;
-
Статистической гипотезой называют:
-
Предположение относительно параметров и вида закона распределения генеральной совокупности;
-
Предположение относительно объема генеральной совокупности;
-
Предположение относительно параметров и вида закона распределения выборки;
-
Предположение относительно объема выборочной совокупности;
-
Предположение относительно статистического критерия ;
-
При проверки статистической гипотезы ошибка первого рода это:
-
Принятие в действительности неверной гипотезы;
-
Отвержение в действительности правильной гипотезы;
-
Принятие в действительности правильной гипотезы;
-
Отвержение в действительности неправильной гипотезы;
-
В критерии Колмогорова за меру качества согласия эмпирического и теоретического распределения принимается:
-
Относительное расхождение между теоретической и эмпирической частотами попадания случайной величины в интервал;
-
Максимальное расхождение по модулю между теоретической и эмпирической частотами попадания случайной величины в интервал;
-
Среднее квадратичное отклонение между теоретической и эмпирической частотами попадания случайной величины в интервал;
-
Максимальное расхождение модуля разности между эмпирической и теоретической функциями распределения;
-
Максимальное расхождение модуля разности между эмпирической и теоретической функциями плотности распределения;
-
Дисперсионный анализ позволяет:
-
Установить степень влияния фактора на изменчивость признака;
-
Установить количество факторов влияния на изменчивость признака;
-
Установить степень влияния факторов на дисперсию;
-
Установить степень влияния фактора на среднее значение;
-
Установить степень влияния фактора на числовые характеристики случайной величины;
-
Задачами регрессионного анализа являются:
-
Выявление связи между случайными величинами и оценка их тесноты;
-
Выявление связи между случайными величинами и их числовыми характеристиками;
-
Выявление уравнения связи между случайными величинами;
-
Выявление уравнения связи между случайной зависимой переменной и неслучайными независимыми переменными и оценка неизвестных значений зависимой переменной;
-
Выявление уравнения связи между неслучайной зависимой переменной и случайными независимыми переменными и оценка неизвестных значений независимой переменной;
-
Выявление уравнения связи между неслучайной независимой переменной и случайными независимыми переменными и оценка неизвестных значений зависимой переменной;
Задачи
-
В урне 6 белых и 4 черных шара. Из нее вынимают подряд 3 шара. Найти вероятность того, что оба шара черные?
-
Продавец мороженного в солнечный день может заработать 10 $., а в дождливый – 3. Чему равна ожидаемая выручка, если вероятность того, что день окажется дождливым, равна 0,4?
-
В банк подано 5 заявок фирм на получение кредита. Вероятность получить кредит для каждой фирмы равна 0,5. Найти вероятность того, что из пяти фирм кредит получит ровно 3 фирмы?
-
Случайная величина задана функцией распределения:

Найти плотность распределения случайной величины и вычислить
вероятность того, что
![]() .
.
-
Коробки с шоколадом упаковываются автоматики чески: средний вес коробки равен 1,06 кГ, а его среднее квадратичное отклонение равно 0,25 кГ. Найти практически возможный максимальный вес одной коробки, если масса коробок поднимается нормальному закону распределения.
-
В урне 2 белых и 7 черных шара. Из нее вынимают подряд 2 шара. Найти вероятность того, что оба шара черные?
-
Продавец мороженного в солнечный день может заработать 5 $., а в дождливый – 2. Чему равна ожидаемая выручка, если вероятность того, что день окажется дождливым, равна 0,5?
-
В банк подано 3 заявок фирм на получение кредита. Вероятность получить кредит для каждой фирмы равна 0,6. Найти вероятность того, что из пяти фирм кредит получит ровно 2 фирмы?
-
Случайная величина задана функцией распределения:

Найти плотность распределения случайной величины и вычислить
вероятность того, что
![]() .
.
-
Коробки с шоколадом упаковываются автоматики чески: средний вес коробки равен 1,0 кГ, а его среднее квадратичное отклонение равно 0,2 кГ. Найти практически возможный максимальный вес одной коробки, если масса коробок поднимается нормальному закону распределения.
-
В урне 4 белых и 4 черных шара. Из нее вынимают подряд 2 шара. Найти вероятность того, что оба шара черные?
-
Продавец мороженного в солнечный день может заработать 12 $., а в дождливый – 6. Чему равна ожидаемая выручка, если вероятность того, что день окажется дождливым, равна 0,8?
-
В банк подано 7 заявок фирм на получение кредита. Вероятность получить кредит для каждой фирмы равна 0,8. Найти вероятность того, что из пяти фирм кредит получит ровно 4 фирмы?
-
Случайная величина задана функцией распределения:

Найти плотность распределения случайной величины и вычислить
вероятность того, что
![]() .
.
-
Коробки с шоколадом упаковываются автоматики чески: средний вес коробки равен 0,5 кГ, а его среднее квадратичное отклонение равно 0,1 кГ. Найти практически возможный максимальный вес одной коробки, если масса коробок поднимается нормальному закону распределения.
-
Из группы деталей делается случайная выборка ( с возвратом) 20 штук. Найти доверительный интервал для генерального среднего с вероятностью 0,95, если результаты выборки представлены в таблице:
Вес деталей, кГ
500
510
520
530
Количество (частота)
3
6
10
1
-
Предполагается произвести выборочное обследование 2000 ламп с целью установления продолжительности их горения. Каким должен быть объем повторной выборки, чтобы можно было гарантировать с вероятностью 0,9, что генеральное среднее отличается от выборочного по абсолютной величине меньше, чем на 20 часов, если генеральная дисперсия меньше 10000 часов.
-
Распределение признака Х в выборке дается следующим вариационным рядом:
|
3,0-3,6 |
3,6-4,2 |
4,2-4,8 |
4,8-5,4 |
5,4-6,0 |
6,0-6,6 |
6,6-7,2 |
|
2 |
8 |
35 |
43 |
22 |
15 |
5 |