
- •Лекция №7
- •Схема решения эл. мех. задачи для форменных мод колебаний
- •Пьезокерамический стержень
- •Пьезокерамический стержень
- •Тонкая пластина
- •Сущность метода эквивалентных схем:
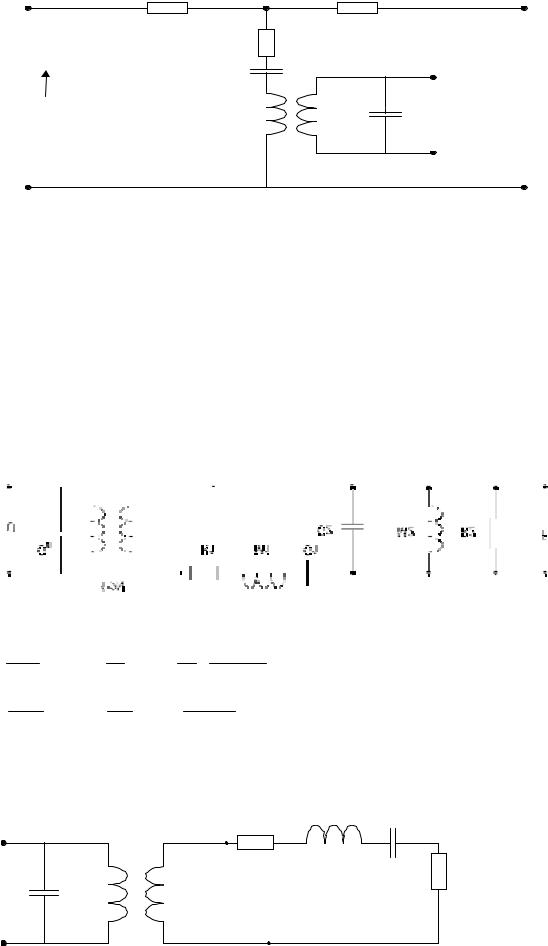
- •5.3.2. Эквивалентная схема ненагруженного кольца
- •5.3.3. Эквивалентная схема нагруженного кольца
- •5.3.7. Упрощения эквивалентных схем
F1 |
F2 |
|
U |
N |
= |
C 0 h 3 3 |
; |
|
С0 |
= |
lw ε3U3 |
; |
|
|
|
|||
|
|
t |
|
|
Z0 = ρV3D ( wl ). |
||||
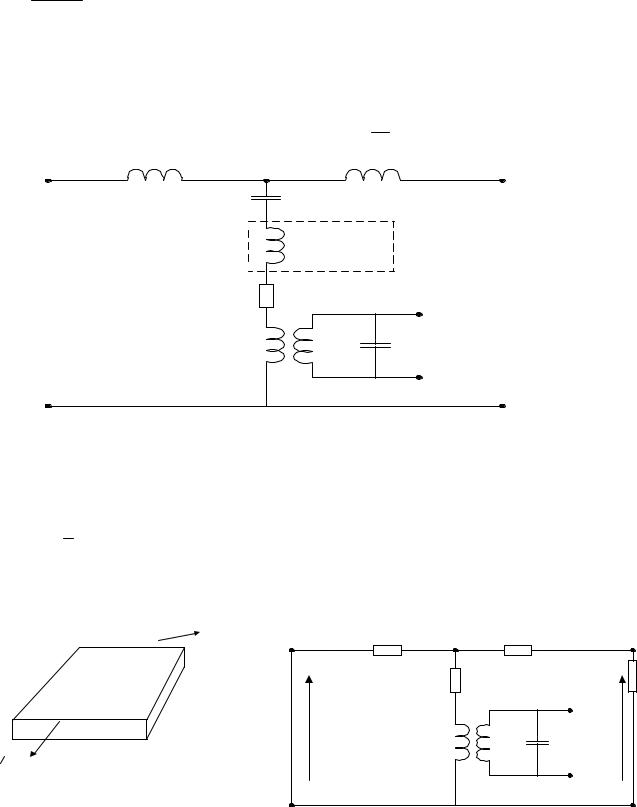
5.3.7. Упрощения эквивалентных схем |
||||
|
|
Вблизи |
основного резонанса, для частот f p ±0,7 f p схема с |
|
распределенными параметрами может быть заменена схемой с сосредоточенными параметрами путем замены тригонометрических функций (sin и tg) первыми двумя членами их разложения в ряд. Образуется схема с комбинацией последовательного и параллельного соединения эквивалентных масс и гибкостей.
Для односторонней нагрузки схема выглядит следующим образом:
R = |
Z π |
; |
|
M |
|
= |
M |
; |
|
C |
|
= |
|
2 |
|
eS E11(33) |
|
|
||
0 |
|
|
|
2 |
|
|
|
|
SK |
|
|
|||||||||
1 |
2QM |
|
|
|
1 |
|
|
|
1 |
|
|
π2 |
|
|
|
|||||
R = |
8Z |
Q |
; |
M |
|
= |
8M |
; |
С |
|
= |
eS E11(33) |
Q = |
ωm |
−добротность..системы |
|||||
0 |
|
|
2 |
|
|
|
|
8SK |
R |
|||||||||||
2 |
π |
|
|
|
|
|
π |
2 |
|
|
2 |
|
|
|
|
|
||||
При присоединении нагрузки ZS << Z11 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
1:2N |
|
|
|
|
|
|
|
|
C1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
C0 |
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
M1 |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zs |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В области частой ниже резонансной f p примерно в 5 раз и более. Аргумент тригнометрических функций kl мал, так, что
tg |
ke |
≈ |
ke |
и sin ke ≈ ke e<<λ |
|
|
|||
2 |
2 |
|
||
В результате чего "Т"-образное звено схемы упрощается вследствие введения сосредоточенных параметровэквивалентной массы и гибкости. М=ρSe-масса стержня
CM = eS E11(33) -механическая гибкость
S
На частотах в области f p , когда колебательный размер хотя и сравним,
но остается меньше длинны волны в материале e<<λ
функцию sin заменяют не аргументом, а двумя членами разложения и тогда в общую ветвь добавляется эквивалентная масса M6 .
-jwM/2 |
CM |
jwM/2 |
-jwM/6
r0 N:1
C0
Все расчетные модели и эквивалентные схемы верны, когда резонансные (колебательные) размеры значительно больше остальных. стержень→↑в 1,5-2 раза цилиндр → высота в 1,5-2 раза меньше резонансного размера, толщина
стенки ≤ 14 диаметра Различные режимы работы.
1. Акт. стержень с одним свободным кон.
F1=0 |
свободный |
z1 |
z1 |
|
конец |
|
|||
|
|
z2 |
|
zs |
|
|
F1 |
U |
F2 |
|
|
|
F2=0
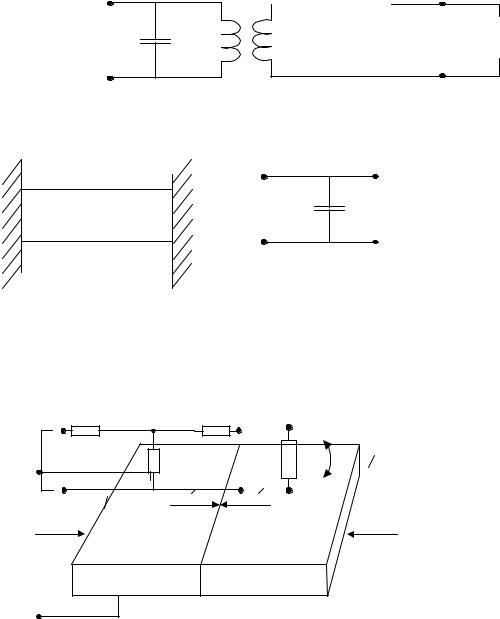
Методами ТОЭ схема упрощается к следующему виду:
1:2N 4z2+2zs
zs
2zs
Вывод: при односторонней нагрузке коэф. трансформации удваивается.
2.Акт. стержень с двумя свободн. концами.
F1=0
F2=0
 U-эл.
U-эл.
выводы
Вывод: ненагруженный эл-т явл. двуполюсником.
3.Акт. стержень с одним закрепленным концом (тяжелая тыльная накладка либо спец.-демпфирование).
U2
F2
F1 = ∞ ; U1 = 0
F1 |
F2 |
|
|
U |
Zs |
||
|
1:N
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
z1 |
|
F2 |
|
|
zs |
|
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4. Акт. стержень с двумя закрепленными концами.
C0 - гибкость
F1 = ∞ ; F2 = ∞;
U1 = 0 ; U2 |
= 0 ; |
|
|
|
|
5. Составной стержень. |
|
|
|
||
z1 |
|
z1 |
|
|
|
F1=0 |
z2 |
F |
=0 |
Z |
F2=0 |
|
|
2 |
|
|
|
|
F1 |
|
|
F2 |
|
F1 |
|
|
|
|
F2 |
U |
1 |
|
|
2 |
|
5. Составной стержень. |
|
|
|
||
1-активный стержень
2-пассивный стержень
жесткое соединение
F1′= F2′
U1′ =U2′ - перемычка
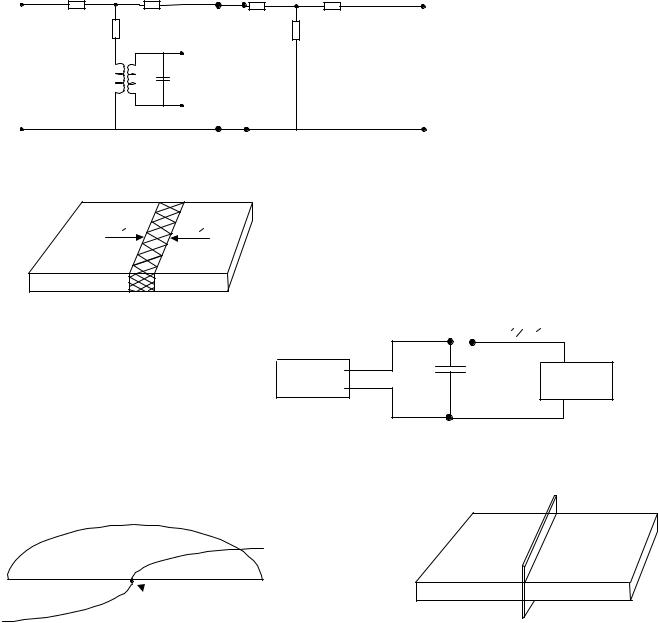
F
F
1
2
Соедин. через акуст. развязку (клей, экран, резина).
F1 F2
|
F1=F2 |
|
А.С. |
учет |
П.С. |
|
гибкости |
|
Учет пласт. крепления
 место крепления
место крепления
