Лекция №7
Схема решения эл. мех. задачи. Эквивалентные схемы преобразователей
Схема решения эл. мех. задачи для форменных мод колебаний
1) Выбор независимых переменных .
Для описания состояния эл. объема можно пользоваться из 4х систем уравнений состояния для пьезоэлектрической среды.
Переменные, описывающие пьезоэлектрик, бывают σ и u и электр. Е
и D.
1.1. Выбор независимых переменных (σ или u).
Оцениваются условия в направлениях перпендикулярных колебательному движению.
НЧ→ σ = 0 - свободный обьем ВЧ→ и = 0 - заторможенный эл-т
1.2. Выбор независимых эл. переменных.(Е или D)
Оцениваются эл. граничные условия в направлении колебательного движения.
Зависят от расположения эл-дов и формы пьезокерамического тела. Для пьезомягких (эл. поле перпендикулярно направлению колебаний,
поверхности эл-дов и колебат. смещению) →Е.
Для пьезожестких (эл. поле параллельно направлению колебаний)
→D.
2)Конструкция ур. состояния.
Анализируются отличные от нуля компоненты D,Е,u,σ . Составляются местные ур. пьезозоэф.
3) Составление ур. движения По третьему закону Ньютона. Рассматрив. элемент. обьем.
F = ma
F-упругая сила→ F = ∂∂σx ;
ma-сила инерции→ ρ ∂2ξ ;ξ −смещение.
∂t 2
Далее выражаем σ из ур. движения. Решение получаем в виде
|
|
wx |
|
wx |
iwt |
|
ξ = |
Аsin |
|
+ B cos |
|
e |
|
ϑ |
|
|
||||
|
|
|
ϑ |
|
||
Находим const А и В из граничных условий.
5) Решение эл. мех. задачи для тока или напряжения. 5.1. Для пьезомягких мод определ. ток I
I = ∫dDdt dS
5.2 Для пьезожестких - напряжение U.
U = −
∫Edz
P.S. И-ю D и напряженность Е находят из ур-я. состояния .
6) Решение эл. мех. задачи для комплексной проводимости (адмитанса) или сопротивления (импеданса).
6.1. Для пьезомягких мод определяем проводимость
Y = UI
6.2. Для пьезожестких мод Z
Z=U/I
Пьезокерамический стержень
3 1
e t 
w
Поперечный пьезоэффект. Эл. поле всегда направлено вдоль оси 3.
1)Эл. поле перпендикулярно мех. колеб. → независимая переменная Е. е>>w>>t → мода НЧ → независимая переменная σ .
2)Выбираем сист. ур. состояния
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = dσ +εσ E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = S Eσ + dt E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = d |
|
σ |
1 |
|
|
+εσ 33 E |
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
= S |
|
|
Eσ |
1 |
|
+ d |
31 |
E |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
3) Составл. ур. движения |
|
1 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
∂2ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
1 |
|
= |
∂σ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
u |
− d |
31 |
E |
3 |
|
∂σ |
|
|
∂ |
|
u |
∂ |
|
|
d |
31 |
E |
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
∂u |
|
|
∂ξ |
|
1 |
|
∂2ξ |
|
|||||||
σ |
1 |
= |
1 |
|
|
; |
|
1 |
= |
|
( |
1 |
) − |
|
|
( |
|
|
|
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= |
u = |
|
= |
|
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
S E11 |
|
|
|
∂x |
|
∂x S E11 |
∂x S E11 |
|
|
|
|
|
|
S E11 |
|
|
|
|
∂x |
|
|
∂x |
|
S11 |
|
∂x2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
∂2ξ1 |
= |
|
|
1 |
|
|
|
∂2ξ1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t 2 |
|
S11E |
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2ξ |
1 |
= |
|
(ϑ, |
E) = |
|
∂ |
2ξ |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
|
||||||||
(ϑ, E)2 = |
1 |
− скорость распространения волн в стержне. |
|
ρS11E |
|||
|
|
3) Получим обычное диф. ур. Его решения -гармоническая функция.
ξ1 |
= ( Аsin |
wx1 |
+ B cos |
wx1 |
)eiwt ; А и В из граничных условий. |
ϑE |
|
||||
|
|
|
ϑE |
||
|
1 |
1 |
|
||
0 |
e/2 |
e |
|
||
|
|
|
σ = 0 / x = 0; x = e для основной моды |
|
|
Далее находятся значения констант, подставляются в общее решение, находят п.5. и 6.
|
|
ew |
|
|
|
|
tg(we / 2ϑ1 E) |
|
|
Y = |
jw |
ε33σ |
[1 |
− k312 |
]+ k312 |
|
|||
t |
we / 2ϑ1 E |
||||||||
|
|
|
|
|
|
|
где k31 −коэф. эл. мех. связи
ε33σ −диэл. прониц. свободного элемента.
ε33σ (1 − k312 ) = ε33u −диэл. прониц. закрепл. эл-та.
На резонансной частоте Im Y=0/
tg |
we |
= ∞; |
we |
= |
π |
→ f p = |
ϑ1 E |
|
2ϑ1 E |
2ϑ1 E |
2 |
2e |
|||||
|
|
|
|
Преобразуем эту формулу.
e = |
ϑE |
|
1 |
= λ / 2 |
|
|
||
|
2 f p |
|
На резонансной длине стержня укладывается пол-длины волны
Пьезокерамический стержень
3
e
продольный эффект
1)E //σ → D
НЧ → σ
2)Используем (3) систему ур.
3)Оставляем компоненты D3 ,σ3 ;
4)Составляем ур-движ. аналогично
только (ϑ3D )2 = |
1 |
− скорость |
|
S33D ρ |
|||
|
|
5) Решение аналогично
ϑD f p = 23e
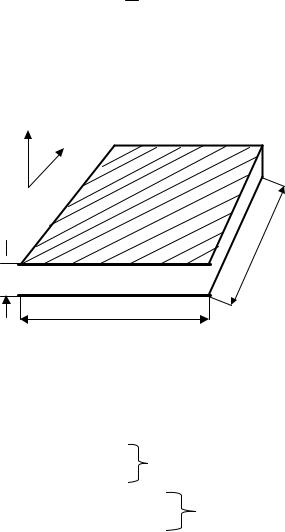
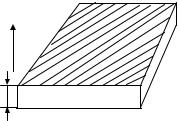
Тонкая пластина
3
t
1) E//σ → D
ВЧ→ u
Используем (4) систему.
2) Используем переменные D3иU3
3) Составляем аналогично ур-движ.
(ϑD )2 |
= |
C D |
33 |
||
|
||
3 |
|
ρ |
|
|
5) Решаем
k222 |
= |
π |
|
|
f p 2t |
ctg |
π f p 2t |
||||||||
2 |
|
ϑ2D |
2 |
ϑ3D |
|
||||||||||
|
|
|
|
|
|
|
|
||||||||
k222 |
= |
π f p t |
ctg |
π f p t |
→ f p |
||||||||||
|
|
|
ϑD |
|
|||||||||||
|
|
|
|
|
|
|
ϑD |
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
fa = |
U D |
|
|
|
|
|
|
|
|
||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
|
2t |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||