3.5.2. Закон Гука при плоскому та об'ємному напружених станах

Розглянемо елемент, виділений з центрально розтягнутого стержня (Рис.3.22).

Елемент зазнає поздовжньої і поперчної деформації, пов'язаної з напруженнями формулами:

; (3.71)

, (3.72)

де  модуль пружності при розтяганні (стисканні), а  коефіцієнт Пуассона. Деформація подовження вважається додатною, скорочення – від’ємною.

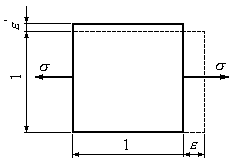
Рис.3.22

Формула (3.71) виражає закон Гука при простому розтяганні (лінійний напружений стан). Встановимо аналогічне співвідношення при об'ємному напруженому стані.

Знайдемо головні деформації , виражаючи їх через головні напруження. Для цього скористаємося принципом незалежності дії сил і співвідношеннями (3.71) і (3.72). Сумарне відносне подовженняза напрямком напруженняможна надати трьома доданками:

,

де  деформація, що виникає при дії тільки напруження , обумовлена формулою (3.71), тому що ця деформація є поздовжньою стосовно(Рис.3.23,а).

подовження, викликане напруженням . Це поперечна деформація стосовно(Рис.3.23,б) і визначається за формулою (3.72).

деформація, що викликана напруженням .

Отже:

.

Застосовуючи подібні міркування до визначення і, одержимо формули закону Гука при об'ємному напруженому стані (узагальнений закон Гука):

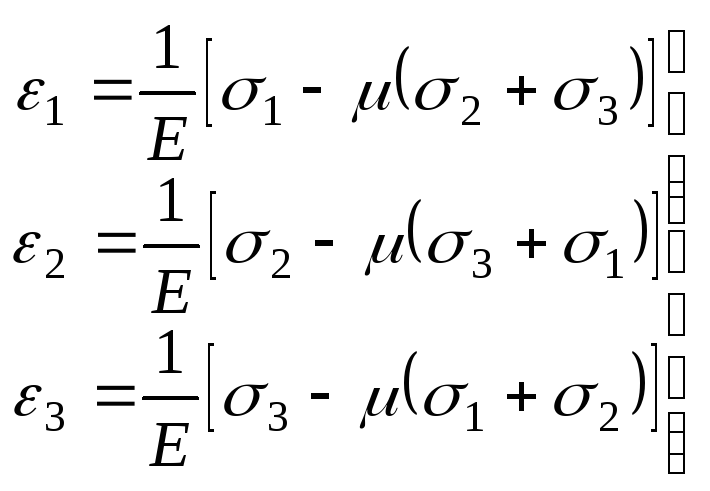(3.73)

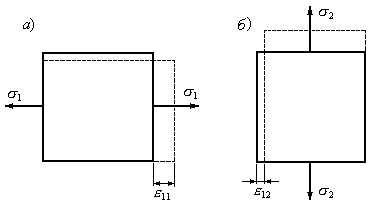
Рис.3.23

Отже:

.

У ці формули розтягальне напруження підставляється зі знаком “+”, а стискальне  зі знаком “”.

При рівності нулю одного з трьох головних напружень маємо плоский напружений стан. У цьому випадку, наприклад, при , одержимо:

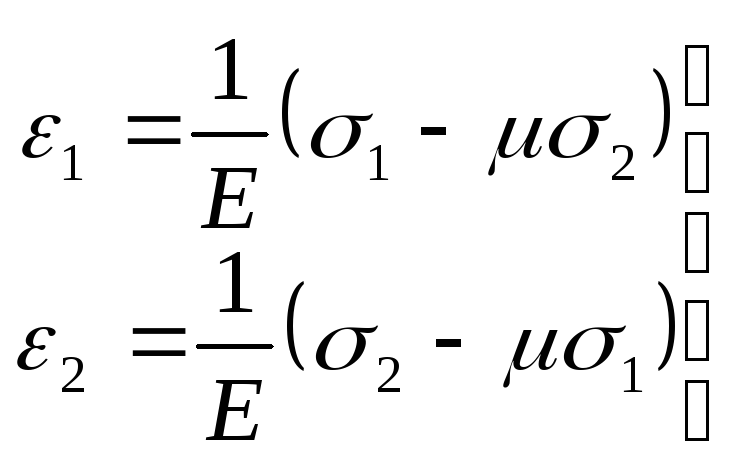(3.74)

Слід зазначити, що рівність нулю напруження не означає, що також дорівнює нулю. Дійсно, примаємо:

. (3.75)

При відомих напруженнях іза формулами (3.74) визначають деформаціїі. Але в деяких випадках необхідно мати зворотну залежність. Умножаючи другий рядок формули (3.74) наі складаючи з першим, одержимо:

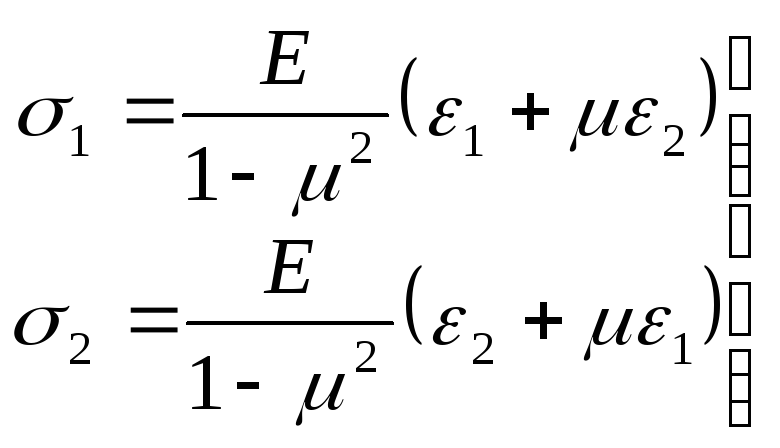(3.76)

Отримані формули написані стосовно до головних площадок і напружень. Однак, варто мати на увазі, що і для неголовних площадок формули, що зв'язують нормальні напруження іі відповідні подовженняі, узагальнений закон Гука має такий саме вигляд:

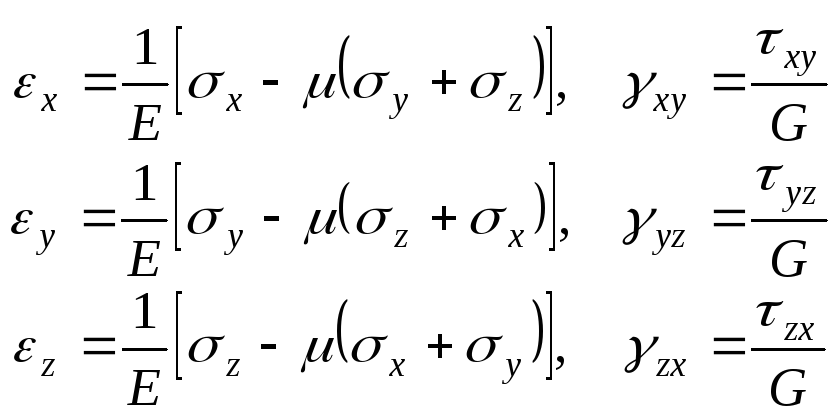, (3.77)

де  модуль зсуву.

Причина полягає в тому, що при малих деформаціях вплив зсуву на лінійну деформацію є величиною другого порядку малості, якою можна знехтувати.

3.5.3.Об'ємна деформація. Об'ємний закон Гука

Позначимо розміри сторін елементарного паралелепіпеда до деформації через (Рис.3.24,а). Після деформації ці розміри збільшаться і дорівнюватимуть,,(Рис.3.24,б). Початковий об’єм паралелепіпеда позначимо , а після деформації.

Знайдемо абсолютну зміну об’єму паралелепіпеда:

, (3.78)

де у дужках позначені відносні подовження:

. (3.79)

Підставляючи в (3.79) у (3.78) і перемножуючи вираз у дужках, одержуємо:

.

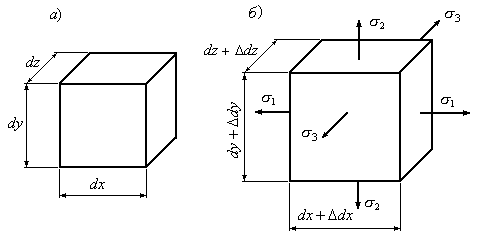
Рис.3.24

Нехтуючи добутками відносних подовжень через їх малість, маємо:

(3.80)

Відносна зміна об’єму, або відносна об'ємна деформація, набуває вигляду:

. (3.81)

Ця формула справедлива як для пружних, так і для пружно-пластичних деформацій.

Для пружної стадії роботи матеріалу можна виразити відносну зміну об’єму через напруження . Для цього підставимо значенняз виразу (3.73) у вираз (3.81):

.

Після перетворення, одержимо:

. (3.82)

Зокрема, при рівномірному всебічному стисканні, коли ,

. (3.83)

З виразу (3.83) випливає, що коефіцієнт Пуассона не може бути більшим за 0,5, тому що в протилежному випадку при всебічному стисканні тіло буде не зменшуватися, а збільшуватися в об’ємі, що суперечить фізичному змістові. Цей висновок підтверджується експериментальними даними. У природі не виявлено матеріалів, у яких коефіцієнт Пуассона був би більший за 0,5.

Існують матеріали (наприклад, парафін), у яких коефіцієнт Пуассона наближається до величини 0,5. У цьому випадку, при всебічному стисканні не буде відбуватися зміна об’єму. Таким чином, парафін за своїми пружніми властивостями наближається до нестисливої рідини.

Для пластичної сталі, що знаходиться у стані текучості, коефіцієнт Пуассона також близький до 0,5. У зв'язку з цим об’єм зразка з пластичної сталі під час текучості не змінюється.

Обчислимо тепер середнє напруження (Рис.3.24,б):

.

Підставляючи середне напруження у формулу (3.82), одержимо:

, (3.84)

де

. (3.85)

Величина називається модулем об'ємної деформації, а вираз (3.84) –об'ємним законом Гука. Відповідно до цього закону відносна зміна об’єму пропорційна середньому напруженню.