3.3.4. Приклади дослідження плоского напруженого стану в точці

Приклад 3.2. Нормальні напруження на площадках = 100МПа,= 60МПа, дотичні напруження= 40МПа. Визначити нормальні,і дотичні,напруження на площадках, нормалі до яких нахилені відносно осіпід кутами відповідноі, якщо=,=(Рис.3.14).

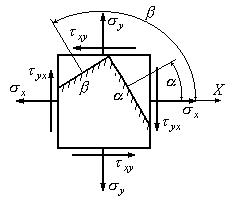
Рис.3.14

Розв’язок:

Для визначення нормального напруження на площадці скористаємося виразом (3.14):

= 55,36МПа.

Нормальне напруження на площадці знайдемо за допомогою виразу (3.15):

= 104,64МПа.

Для перевірки використовуємо умову інваріантності (3.16):

55,36 + 104,64 = 100 + 60 = const.

Дотичне напруження визначимо з виразу (3.12):

МПа.

Дотичне напруження, що діє на площадці :

МПа.

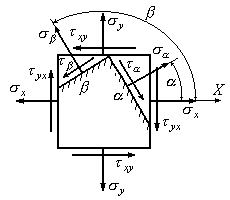
Рис.3.15

У відповідності до закону парності дотичних напружень (3.8):

.

Отже, задача вирішена правильно. Напрямки нормальних і дотичних напружень, що діють на площадках і, наведені на рис. 3.15.

Приклад 3.3. Визначити величини головних напружень іта напрями головних напружень (Рис.3.16,а). Зобразити головні площадки і головні напруження на рисунку.

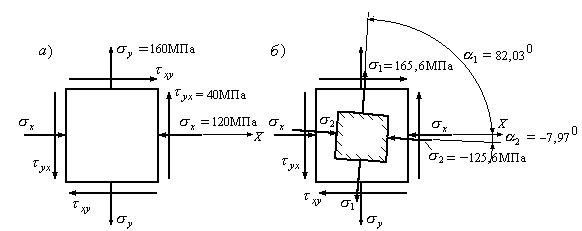
Рис.3.16

Розв’язок:

1. Визначаємо екстремальні нормальні напруження з виразу (3.19):

=

=165,6МПа.

=125,6МПа.

Для перевірки використовуємо умову інваріантості (3.16):

165,6125,6=120+160= const.

Напрямки головних напружень знайдемо, використовуючи вираз (3.20):

; 82,03⁰;

;  7,97⁰ .

Для перевірки правильності розв’язку складемо абсолютні величини кутів і. Зважаючи на те, що головні осі взаємно перпендикулярні, у сумі має вийти кут 90⁰:

82,03⁰ +7,97⁰ = 90⁰.

Розв’язок виконаний правильно. Відкладемо знайдені кути на рис.3.16,б і проставимо значення головних напружень.

3.4. Об'ємний напружений стан

3.4.1. Поняття про тензор напружень. Екстремальні дотичні напруження

Випадок об'ємного напруженого стану наведений на рис.3.2: на кожній з граней діють нормальні напруження , а також по дві складові дотичних напружень.

Таким чином, напружений стан у виділеному елементарному паралелепіпеді в загальному випадку характеризується дев'ятьма компонентами напружень, що можуть бути записані у вигляді тензора напружень:

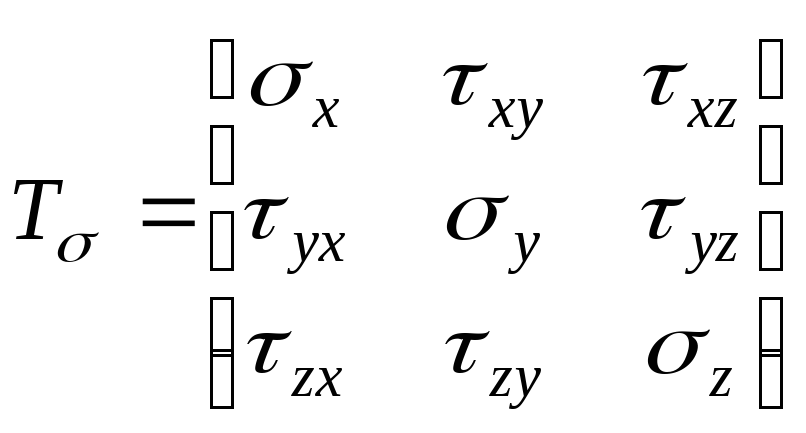(3.25)

Дотичні напруження, надані тензором напружень, зв'язані кількома залежностями, одержати які можна, склавши рівняння суми моментів усіх сил відносно координатних осей (Рис.3.2):

;;.(3.26)

Модулі цих напружень однакові, а знаки на підставі закону парності дотичних напружень (3.8) протилежні.

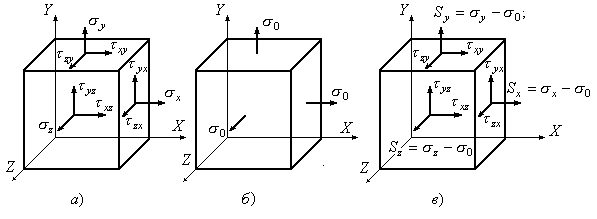
Рис.3.17

Загальний випадок напруженого стану (Рис.3.17,а) може бути наведений у вигляді суми двох напружених станів, що характеризуються у першому випадку однаковими нормальними напруженнями (Рис.3.17,б) і в другому випадку (Рис.3.17,в) – нормальними напруженнями:

; ;(3.27)

та дотичними напруженнями .

Приймемо:

. (3.28)

Тоді з (3.27) випливає:

. (3.29)

Напружений стан, наведений на рис.3.17,б, може бути описаний кульовим тензором напружень:

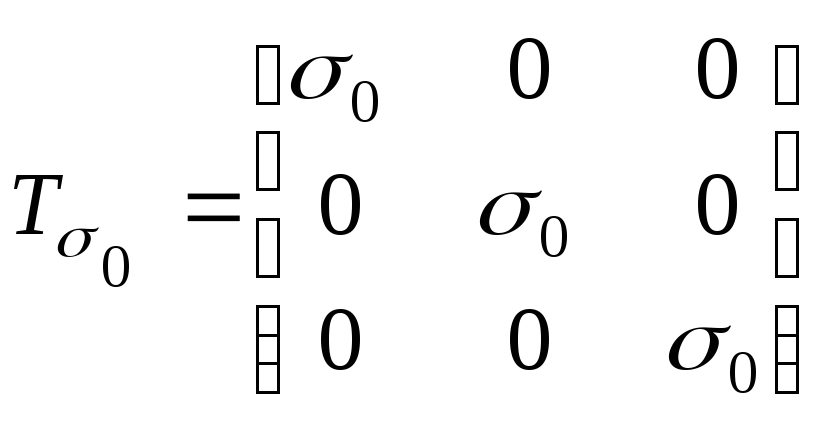(3.30)

Напружений стан, наведений на рис.3.17,в, може бути описаний тензором, що називається девіатором напружень:

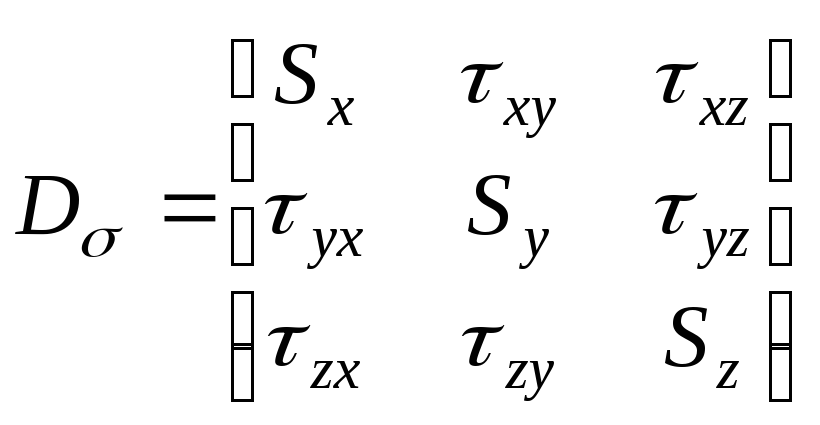(3.31)

Кульовий тензор характеризує зміну об’єму виділеного елемента, девіатор характеризує зміну форми елемента.

Розглянемо визначення головних напружень і, через напруження, що діють на довільних площадках (Рис.3.17,а). Припустимо, що нам відоме положення головної площадки, обумовлене нахилом нормалі до цієї площадкистосовно осей координат. Перерізом, паралельним цій площадці, виділимо з вихідного паралелепіпеда тетраедр, зображений на рис.3.18, і складемо умови рівноваги тетраэдра у вигляді сум проекцій усіх сил, що діють на тетраедр, на осі координат.

Косинуси кутів, утворені нормаллю з осями координат, позначимо відповідно. Приймемо площу похилої грані, тоді площі інших граней, що лежать у координатних площинах, будуть,,. На головній площадці дотичні напруження відсутні. Головне напруження, що діє на цій площадці, позначимо через. Сума проекцій сил на вісьдає[6]:

.

Рис.3.18

Проектуючи всі сили на осі та, одержимо ще два аналогічні рівняння. Таким чином, будемо мати наступні три рівняння рівноваги тетраедра:

(3.32)

Рівняння (3.32) можна розглядати як однорідну систему рівнянь відносно невідомих . Між направляючими косинусами нормалііснує залежність:

, (3.33)

тому вони не можуть одностайно дорівнювати нулю. Відомо, що при цій умові визначник системи (3.32) має дорівнювати нулю, тобто

. (3.34)

Розкривши визначник (3.43), приходимо до кубічного рівняння:

, (3.35)

три корені якого являють собою головні напруження .

Коефіцієнти рівняння (3.35) набувають вигляду:

; (3.36)

; (3.37)

. (3.38)

Оскільки головні напруження не залежать від вибору осей координат, коефіцієнти кубічного рівняння (3.35) також не змінюються при повороті осей координат, тобто є інваріантами і називаються відповідно, першим , другимі третімінваріантами тензора напружень. З формул (3.36)(3.38) випливає, що вираз інваріантів тензора напружень через головні напруження має вигляд:

; (3.39)

; (3.40)

. (3.41)

В окремому випадку плоского напруженого стану кубічне рівняння (3.35) зводиться до квадратного, два корені якого дають значення і, що збігається з формулами (3.19), отриманими вище. У цьому випадку потрібно покласти, тому що граньвихідного паралелепіпеда має бути вільною від напружень.

Для визначення направляючих косинусів і, що відповідають одному з трьох головних напруженьта, потрібно значення цього головного напруження підставити у вираз (3.32) замість. Спільне вирішення рівнянь (3.32) дає шукані величиниі.

Для визначення максимальних дотичних напружень приймемо, що головні напруження івідомі. Як і при плоскому напруженому стані максимальні дотичні напруження діють у площадках, нахилених під кутом 45⁰ до головних напружень. Дотичні напруження на цих площадках матимуть вигляд:

; ;. (3.42)

Найбільше з цих напружень визначає максимальні дотичні напруження в точці:

. (3.43)

Таким чином, у загальному випадку максимальне дотичне напруження в точці діє на площадці, нахиленій під кутом 45⁰ до максимальних і мінімальних з трьох головних напружень, і дорівнює їх напіврізниці.

Міцність матеріалу або перехід його під навантаженням у пластичний стан у ряді випадків пов'язують з величиною максимального дотичного напруження , і тому воно поряд з головними напруженнями є важливою характеристикою напруженого стану.