3.3.2. Обчислення величин головних напружень і визначення положення головних площадок

Дослідимо вираз для нормальних напружень (3.14) на екстремум. Для цього візьмемо похідну від напруження поі дорівнемо нулю:

, (3.17)

де  кут, що складає нормаль до розглянутої площадки з додатним напрямом осі , при якому нормальне напруженнясягає найбільшого значення для даної точки.

Вираз (3.17) являє собою величину дотичного напруження в головній площадці . Таким чином, дотичне напруження в розглянутій площадці () дорівнює нулю. Звідси робимо висновок: площадка, нормаль до якої складає кутз додатним напрямком осі, є головною площадкою.

Дорівнюючи вираз у дужках формули (3.17) нулю, знайдемо тангенс подвійного кута, що визначає нахил головних площадок:

. (3.18)

Вираз (3.18) дає два взаємно перпендикулярних напрямки з кутами нахилу і, за якими діють головні напруження (Рис.3.12).

Для визначення величин головних напружень підставимо формулу (3.14) . Виносячиза дужку, одержимо:

. (а)

З тригонометрії відомо:

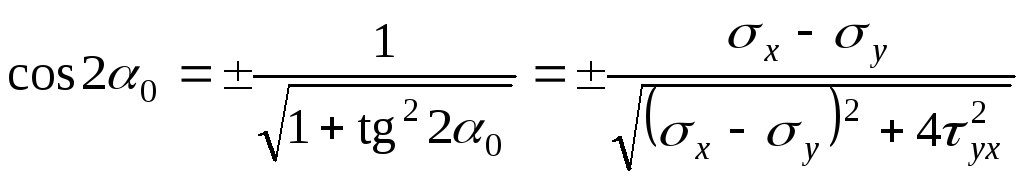. (б)

Знаки поставлені тому, що косинуси кутівімають протилежні знаки. Підставляючи (3.18) у (б) і (а), одержимо:

.

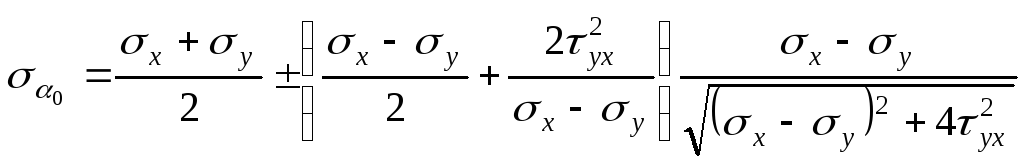
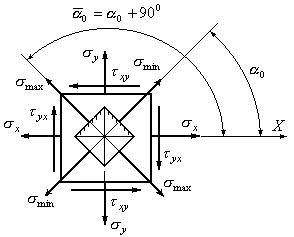
Рис.3.12

У цій формулі знак “+” відповідає максимальному головному напруженню , а знак “” відповідає мінімальному головному напруженню. Таким чином, остаточно маємо:

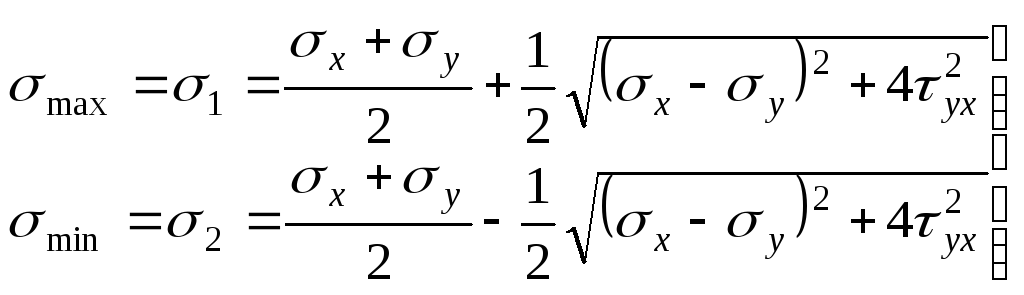(3.19)

З наведеного висновку випливає, що при будь-яких вихідних напруженнях у даній точці існує паралелепіпед, на гранях якого діють тільки нормальні напруження.

Повернемося до формули (3.18). Вона дає два головних напрямки, але не вказує, у якому з них діє , а в якому . Для розв’язання цього питання треба було б дослідити знак другої похідної приі. Однак, можна розв’язати цю задачу, використовуючи вирази, подібні до тих, що застосовувються для визначення напрямків головних осей інерції в розділі “Геометричні характеристики плоских фігур” [6]:

, 3.20)

де  кут, який треба відкласти від додатного напрямку осі до нормалі до площадки, у якій діє максимальне нормальне напруження; кут, який треба відкласти від додатної осі до нормалі до площадки, у якій діє мінімальне нормальне напруження. Додатний кут слід відкладати проти годинникової стрілки, від’ємний – за годинниковою стрілкою.

Для контролю правильності визначення положення головних площадок можна використовувати ще один спосіб, наведений у [6]. Виходячи з того, що з поворотом площадки в напрямку вектора дотичних напружень нормальне напруження на площадці алгебраїчно зростає, у роботі [6] формулюється наступне правило: напрямок завжди проходить через дві чверті координат, у яких стрілки дотичних напруженьізбігаються.

3.3.3. Екстремальні дотичні напруження

Приймемо в якості вихідних головні площадки, тобто такі, у яких діють головні напруження (Рис.3.13).

Рис.3.13

Відраховуючи кут від напрямку, напишемо вираз дляі, використовуючи формули (3.12), (3.14), припускаючи в них,, а:

; (3.21)

. (3.22)

З формули (3.22) випливає, що при дотичні напруження мають екстремальні значення:

. (3.23)

Екстремальні дотичні напруження у точці дорівнюють напіврізниці головних напружень і діють на площадках, нахилених до головних під кутом 45⁰ (Рис.3.13,а).

Підставляючи (3.19) у (3.23), одержимо вираз для через вихідні напруженнята:

. (3.24)

В окремому випадку, коли на межах призми діють два головних напруження (Рис.3.13,б), екстремальні дотичні напруження (3.23) чисельно дорівнюють головним напруженням:

,

а нормальні напруження на площадках з екстремальними дотичними напруженнями у цьому випадку дорівнюють нулю. Такий випадок напруженого стану називається чистим зсувом, а площадки, на яких діють тільки дотичні напруження, називаються площадками чистого зсуву.