5. Правило лопіталя
5.1. При
розкритті невизначеностей
,
крім класичних методів обчислення
границь, у багатьох випадках можна
користуватися правилом Лопіталя:
якщо
або
й існує
границя
відношення
їх похідних
,
то
.
Це правило
справедливе й у випадку, коли
.
Приклад 1. Застосовуючи правило Лопіталя, знайти границі:
а)
;б)
;в)
.
Розв’язання.
Переконавшись, що має місце випадок
або
,
застосовуємо правило Лопіталя.
а)
,
б)
.
Тут двічі було застосовано правило Лопіталя й використана перша чудова границя.
в)
.
5.2.
При розкритті невизначеностей
для застосування правила Лопіталя,
початковий вираз необхідно перетворити
до невизначеностей виду
або
шляхом алгебраїчних перетворень.
Приклад
2. Знайти
границі:
а)
;б)
.
Розв’язання:
а)
Маємо невизначеність
.
Наведемо цю невизначеність до
невизначеності
,
а потім застосуємо правило Лопіталя:
.
б)
Маємо невизначеність
.
Перетворимо початковий вираз до
невизначеності
,
після чого застосуємо правило Лопіталя:
.
5.3.
При розкритті невизначеностей
,
,
рекомендується знайти попередньо
границю логарифма шуканої функції.
Приклад
3.Обчислити
.
Розв’язання.
Маємо
невизначеність
.
Введемо позначення
,
тоді
.
.
Одержали
,
застосовуємо правило Лопіталя:
.
Тому що
.
Отже
.
Завдання 6. Обчислити границі, використовуючи правило Лопіталя.
|
|
а)
|
б)
|
|
|
а)
|
б) |
|
|
а)
|
б)
|
|
|
а)
|
б) |
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а) |
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б) |
|
|
а)
|
б) |
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б) |
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
|
а)
|
б)
|
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.Список літератури
|
|
Берман Г.Е. Сборник задач по курсу математического анализа. – М.: Наука, 1977. – 456 с. | |
|
|
Бронштейн И.Н., Семендяев К.А. Сравочник по математике для инженеров и студентов ВУЗов. – М.: Наука, 1986. – 544 с. |
|
|
|
Бубняк Т.І. Вища математика: Навчальний посібник. – Львів: «Новий світ-2000», 2004. – 434 с. |
|
|
|
Вища математика: Підручник: У 2 кн. – 2-ге вид., перероб. і доп. – К.: Либідь, 2003. – Кн. 1. Основні розділи / Г.Й. Призва, В.В. Плахотник, Л.Д. Гординський та ін.; за ред. Г.Л. Кулініча. – 400 с. |
|
|
|
Вища математика. Основні означення, приклади і задачі. Ч. 1, 2. – К.: Либідь, 1992. – 349 с. | |
|
|
Глушков П.М., Шунда Н.М. Диференціальне числення фукнцій однієї змінної. – К.: Вища шк., 1991. – 343 с. | |
|
|
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1,2 – М.: Высш. шк., 1980. – 320 с. | |
|
|
Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966. – 269 с. | |
|
|
Каплан И.А. Практические занятия по высшей математике. – Харьков.: Изд-во ХГУ, 1967. – 236 с. |
|
|
|
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1969. – 123 с. |
|
|
|
Мантуров О.В., Матвеев Н.М. Курс высшей математики. – М.: Высш. шк., 1986. – 296 с. |
|
|
|
Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1969. – 350 с. |
|
|
|
Овчинников П.Ф., Яремчук Ф.П., Михайленко В.М. Высшая математика. Ч.1, 2. – К.: Вища шк., 1987, 1989. – 551 с. |
|
|
|
Пискунов Н.С. Дифференциальное и интегральное исчисление, т.1, 2. – М.: Наука, 1982. – 294 с. | |
|
|
Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики. – М.: Высш. шк., 1987. – 320 с. |
|
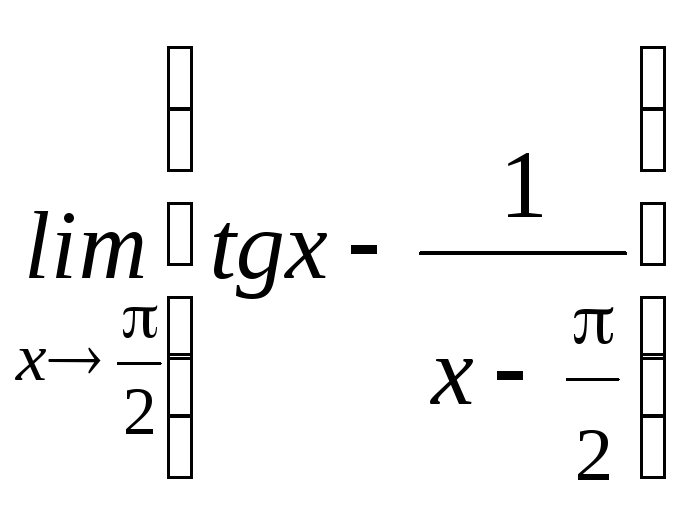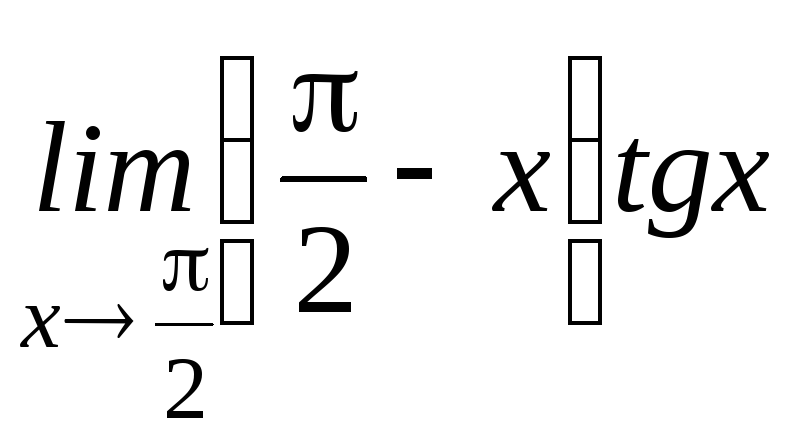