
- •Методичні вказівки та індивідуальні завдання
- •Відповідальний за випуск д.Г. Зеленцов, д-р техн. Наук
- •Основні питання програми дисципліни за темою «диференціальне числення функцій однієї змінної»
- •Орієнтовний перелік питань для підсумкового контролю знань
- •1. Визначення похідної. Диференціювання функцій
- •1.3. Таблиця похідних функцій:
- •2. Геометричне застосування похідної
- •3. Диференціювання функцій, заданих параметрично
- •5. Правило лопіталя
- •Список літератури
3. Диференціювання функцій, заданих параметрично
3.1.Якщо функція![]() задана параметрично двома рівняннями
задана параметрично двома рівняннями![]() ,
,![]() ,
,![]() ,
то її похідні обчислюються за формулами:
,
то її похідні обчислюються за формулами:
![]() ,
,
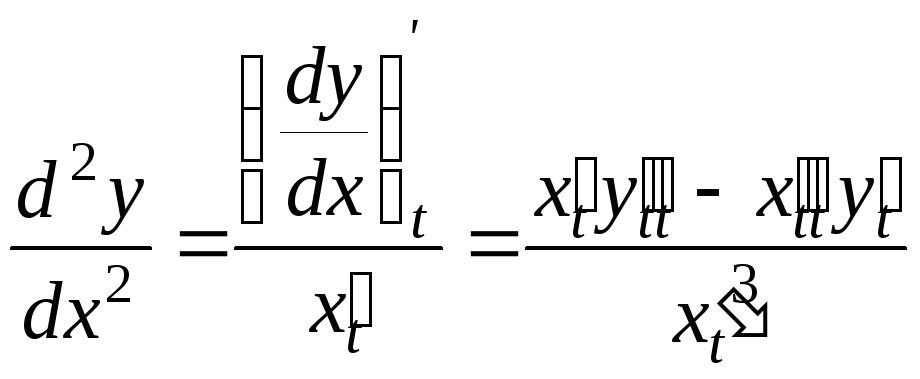 .
.
3.2.Приклади.а) Знайти![]() й
й![]() ,
якщо функція
,
якщо функція![]() задана параметрично:
задана параметрично:![]()
![]() .
.
Розв’язання.
Послідовно знаходимо похідні:
![]() ,
,![]() ;
;![]() ,
,![]() ;
;
![]() ;
;
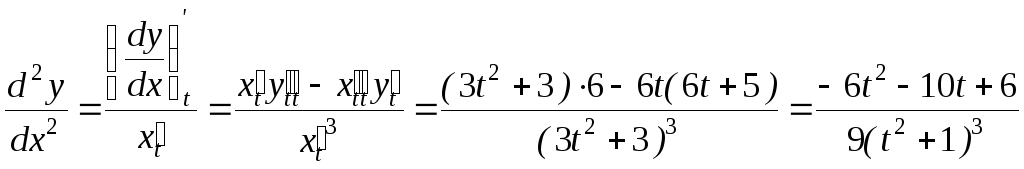 .
.
б) Написати рівняння
дотичної до кривої
![]() у точці
у точці![]() .
.
Розв’язання. Рівняння дотичної шукаємо у вигляді:
![]()
де
![]() ;
;![]() .
.
Знайдемо
![]() при
при![]() .
Так як
.
Так як
![]() ,
,
![]() ,
,
то
![]()
![]() ,
томy
,
томy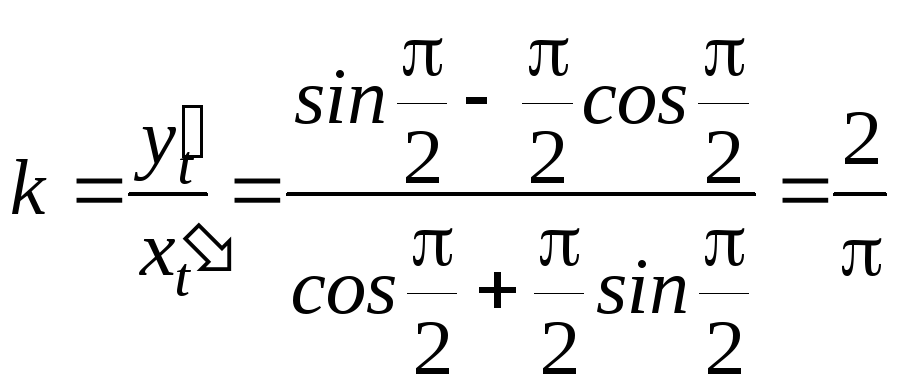 при
при![]() і рівняння дотичної має вигляд:
і рівняння дотичної має вигляд:![]() .
.
Завдання
3.Для функцій, заданих параметрично,
знайти першу![]() та другу
та другу![]() похідні.
похідні.
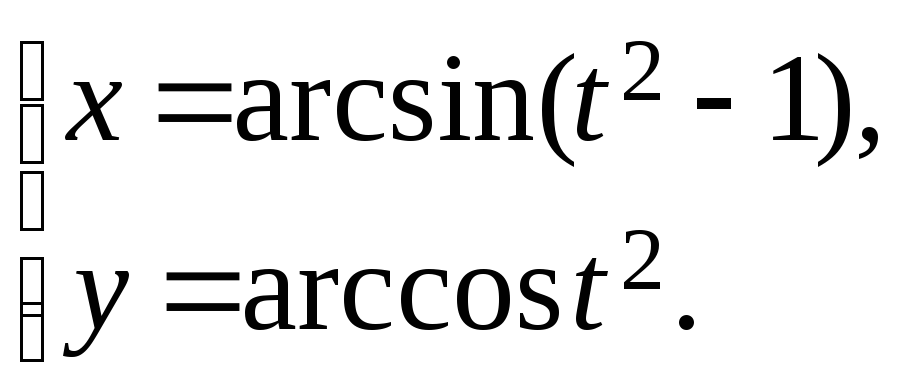 11.
11.
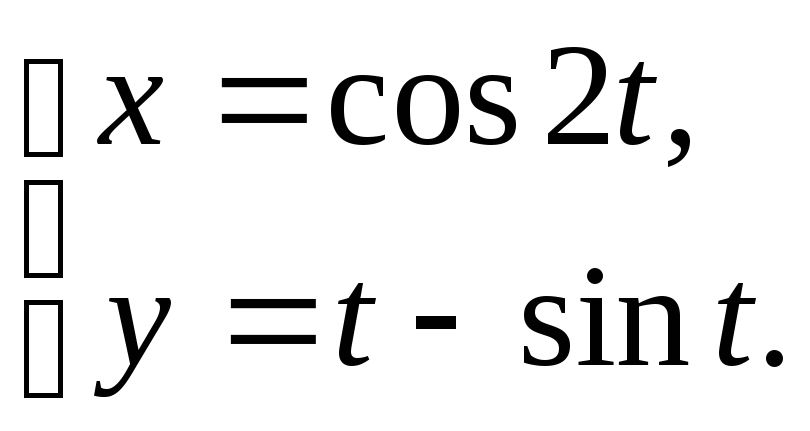 21.
21.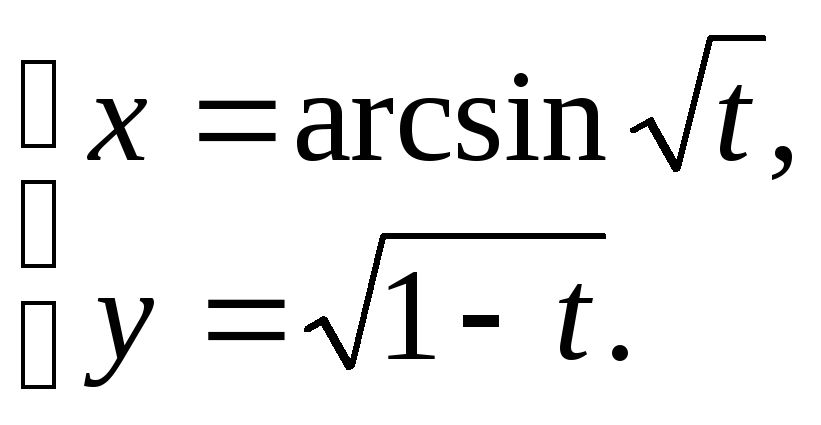
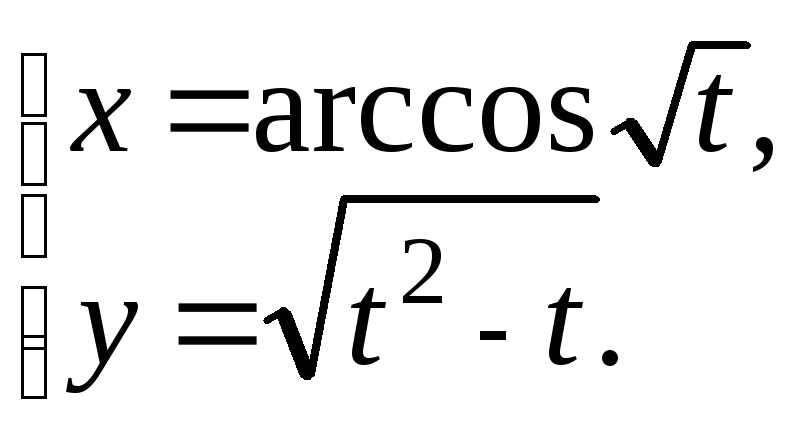 12.
12.
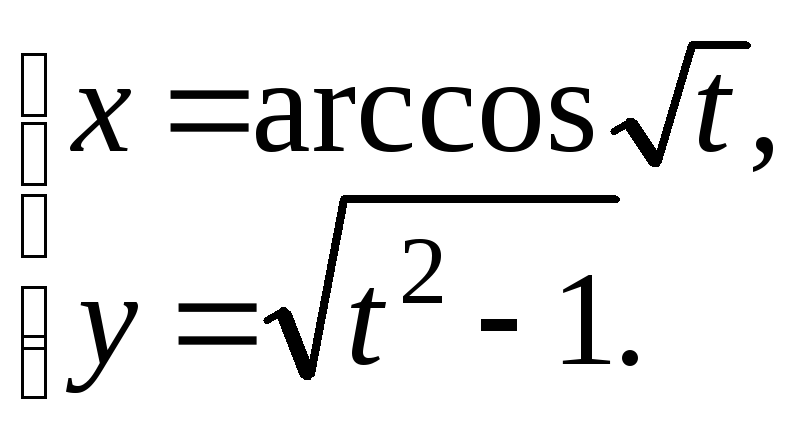 22.
22.
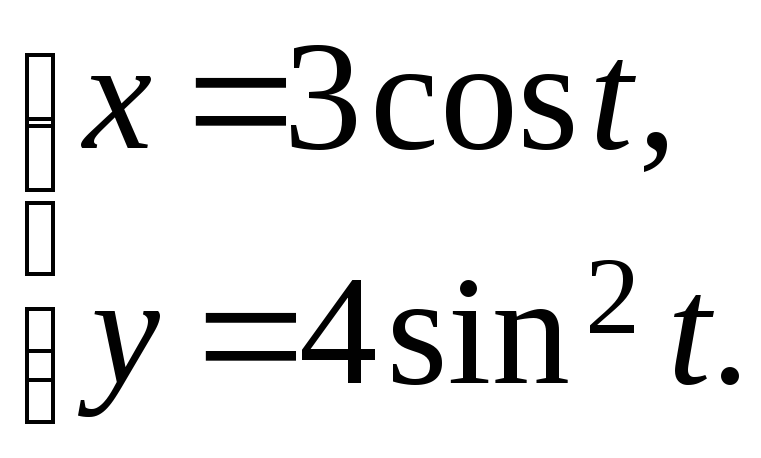
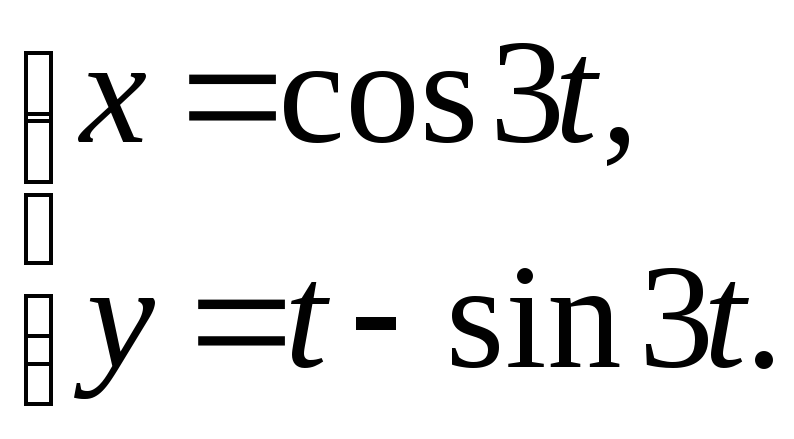 13.
13.
 23.
23.
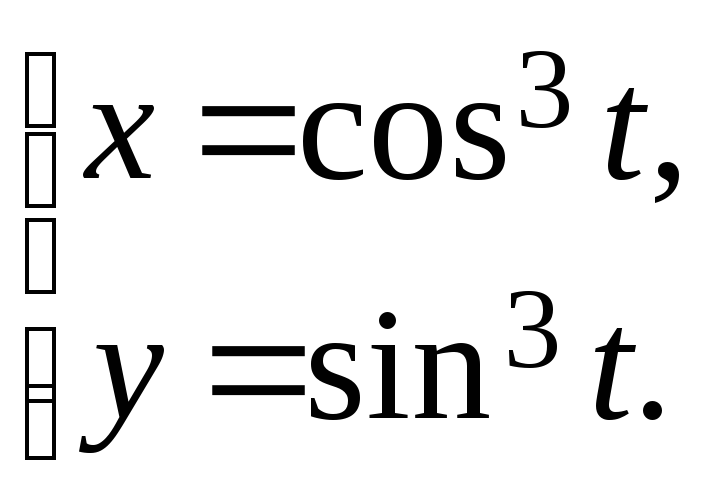
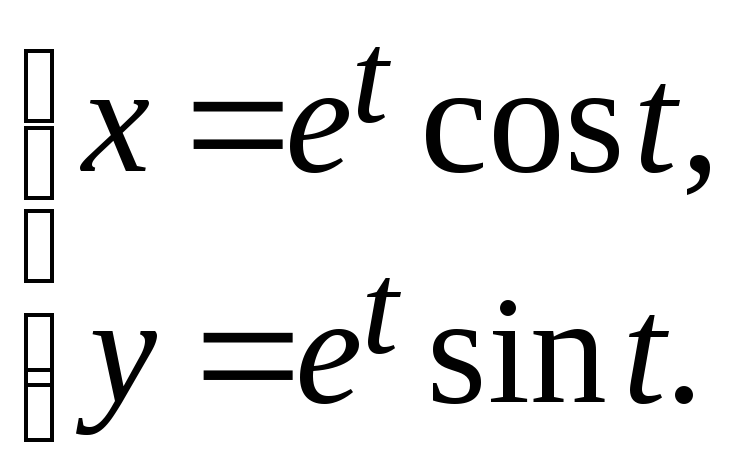 14.
14.
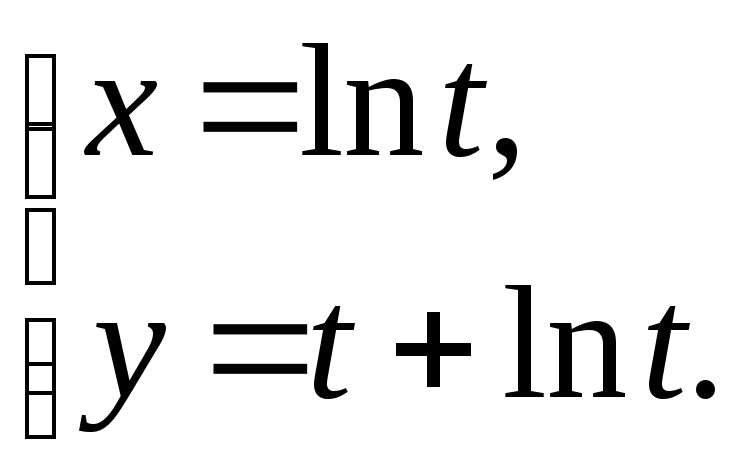 24.
24.
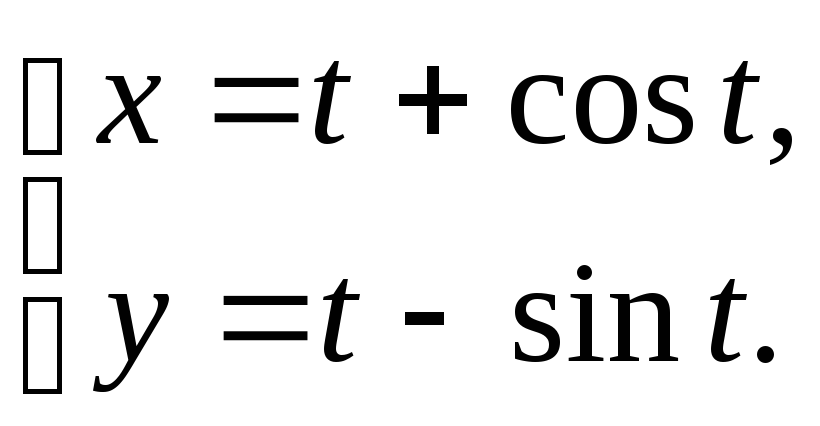
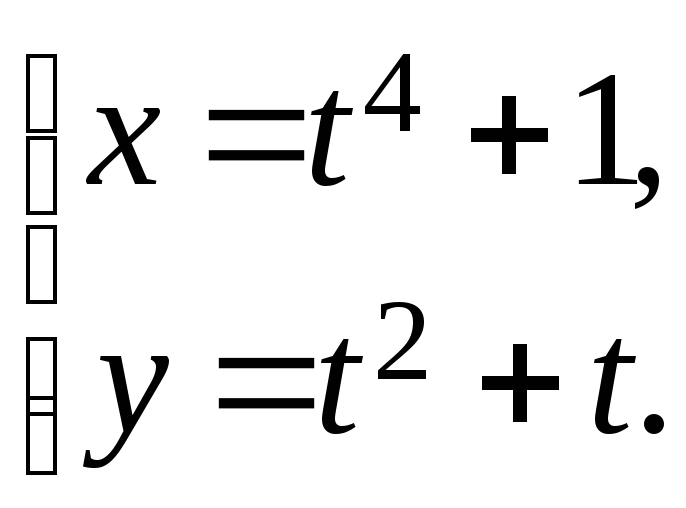 15.
15.
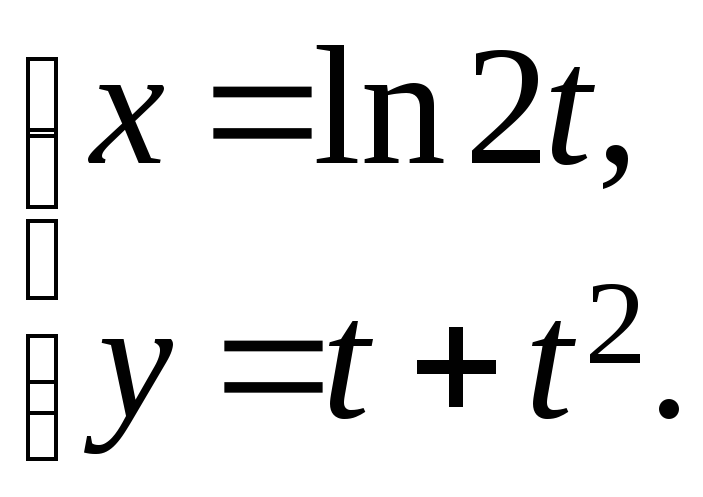 25.
25.

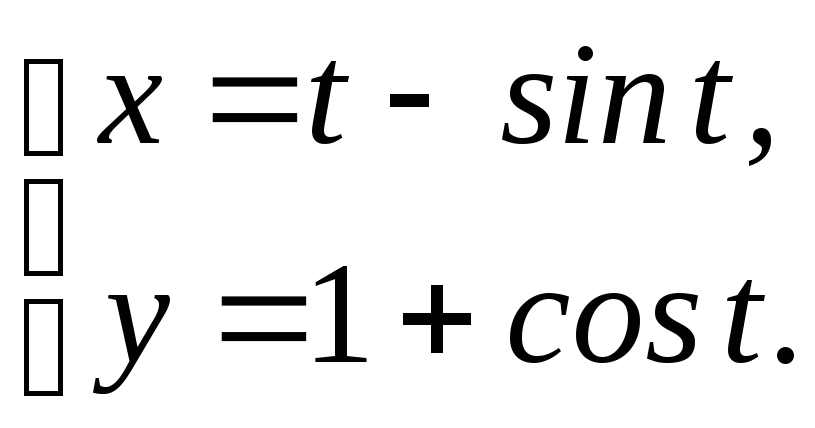 16.
16.
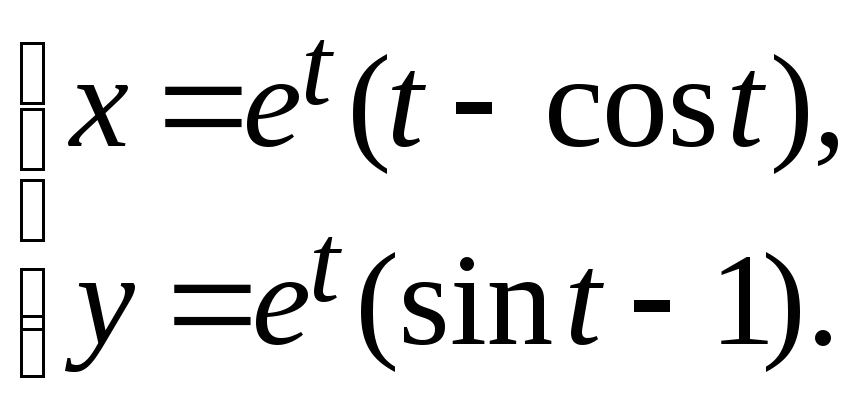 26.
26.
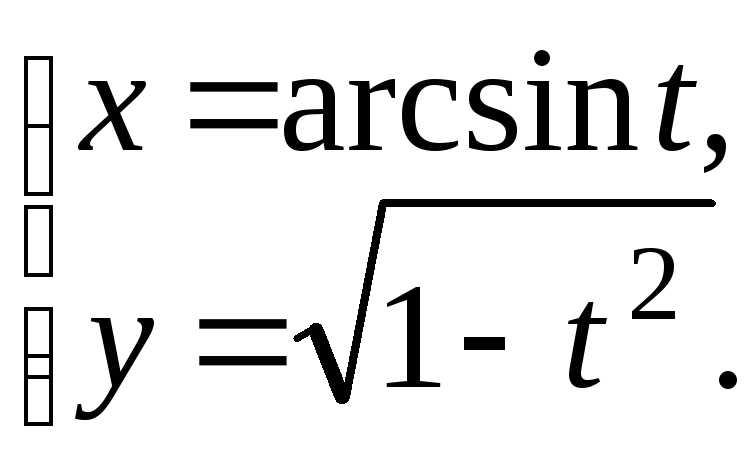
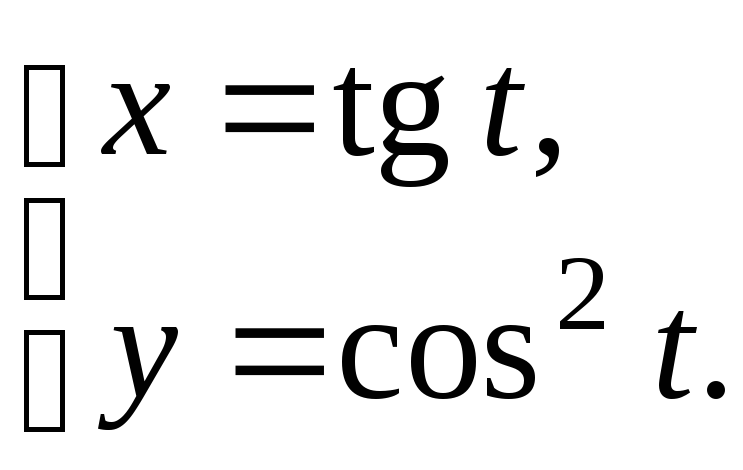 17.
17.
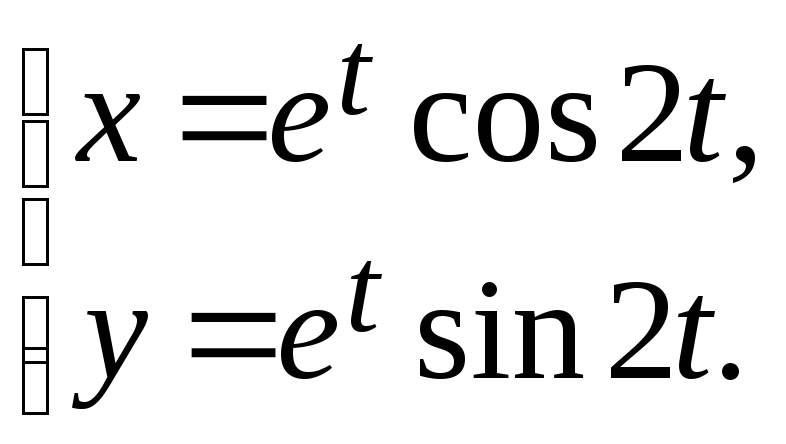 27.
27.
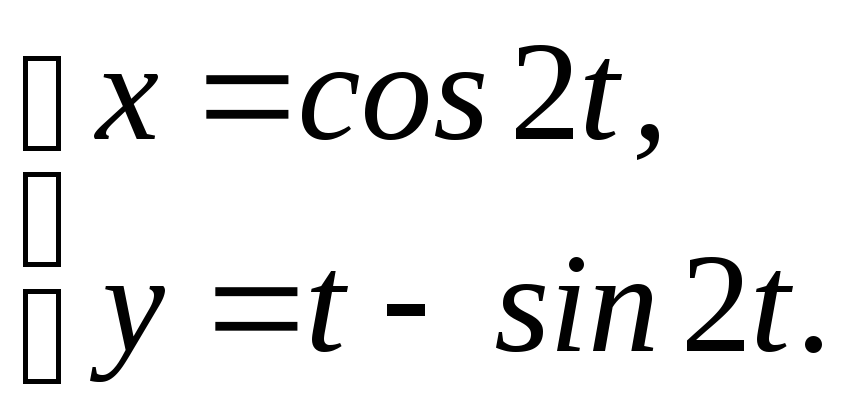
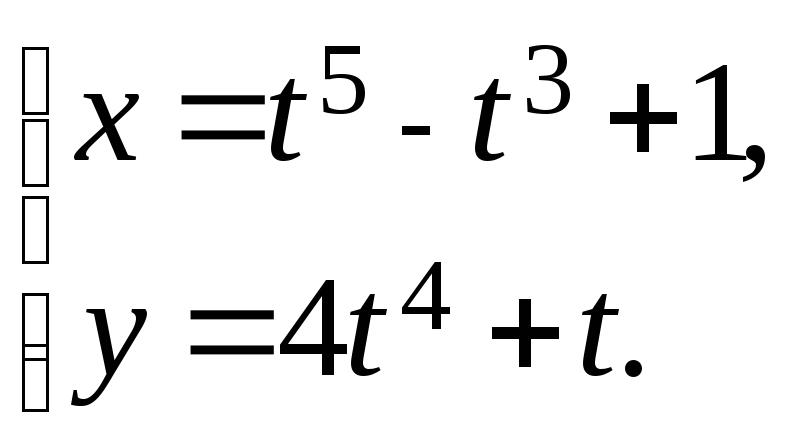 18.
18.
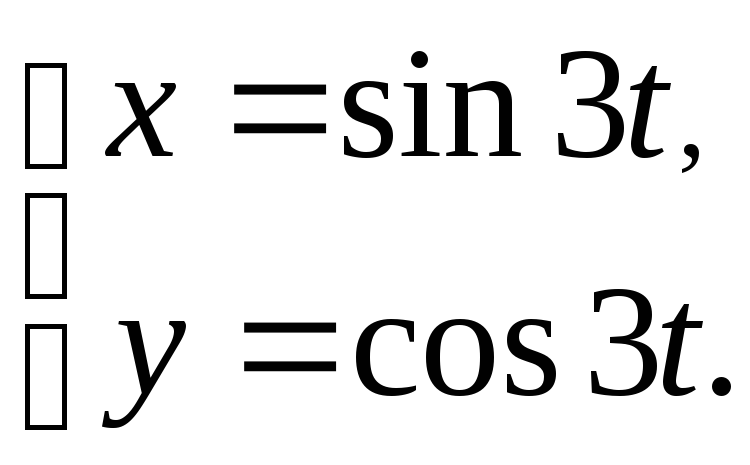 28.
28.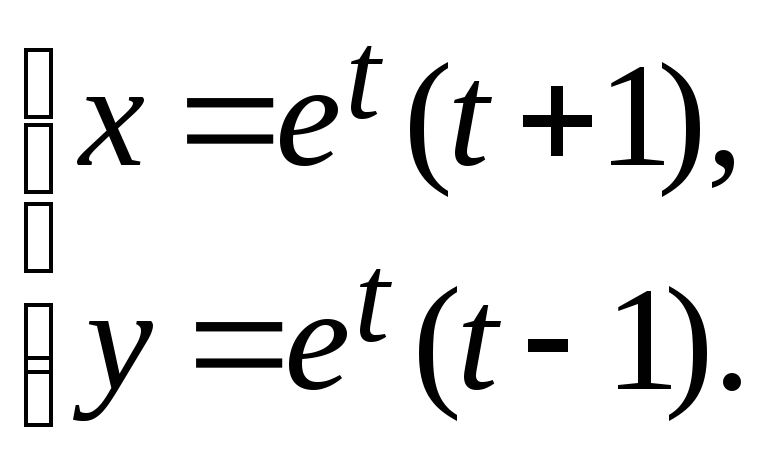
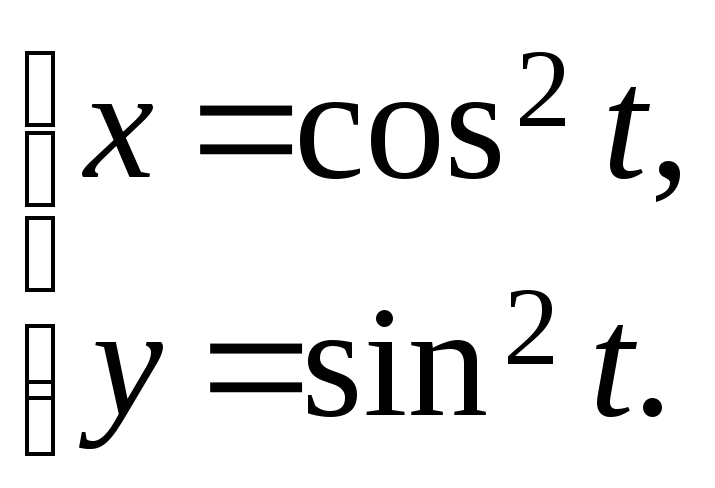 19.
19.
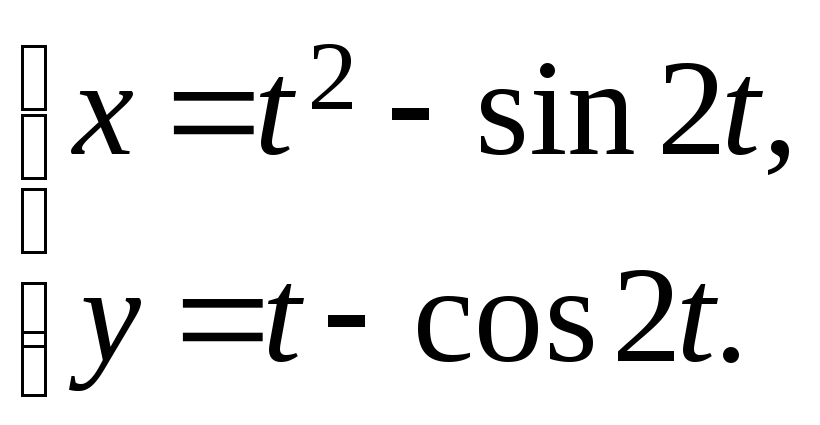 29.
29.
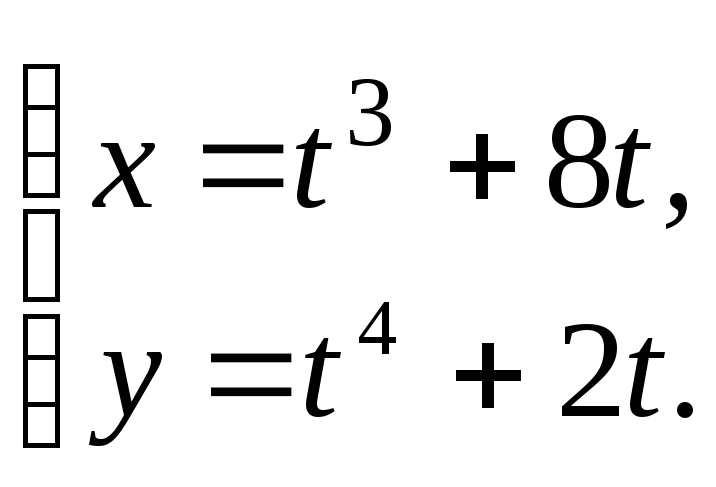
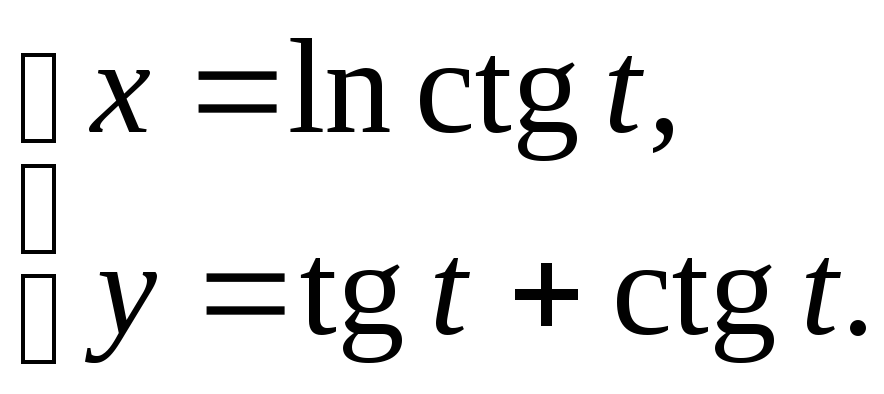 20.
20.
 30.
30.
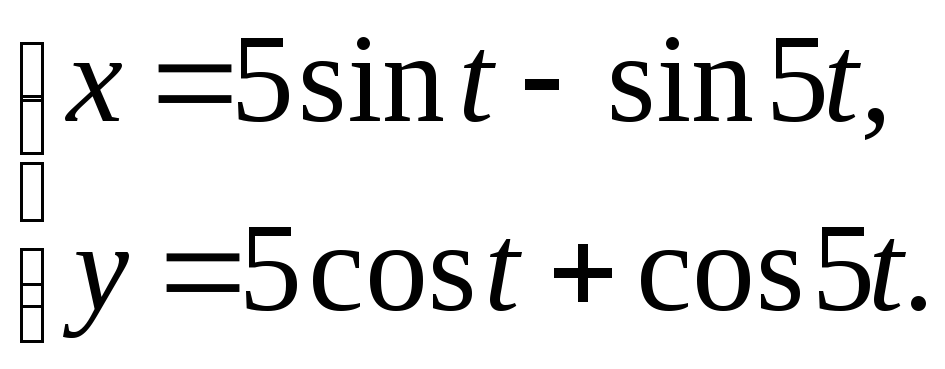
4. ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ, ЗАДАНИХ НЕЯВНО
4.1.Рівняння![]() задає неявно функцію
задає неявно функцію![]() ,
на інтервалі
,
на інтервалі![]() ,
якщо для всіх
,
якщо для всіх![]() виконується рівність
виконується рівність![]() .
.
Для обчислення
похідної функції
![]() треба продиференціювати по
треба продиференціювати по![]() тотожність
тотожність![]() ,
пам'ятаючи, що
,
пам'ятаючи, що![]() є функція від
є функція від![]() ,
а потім отримане рівняння розв’язати
відносно
,
а потім отримане рівняння розв’язати
відносно![]() .
.
4.2. Приклади.а) Знайти значення![]() у точці
у точці![]() для функції, заданої неявно рівнянням
для функції, заданої неявно рівнянням![]() .
.
Розв’язання.
Диференціюючи по
![]() обидві частини даного рівняння та
вважаючи при цьому, що
обидві частини даного рівняння та
вважаючи при цьому, що![]() є функцією від
є функцією від![]() ,
одержуємо:
,
одержуємо:
![]() ,
,
звідки:
![]() .
.
Знаходимо значення
![]() у точці
у точці![]() :
:
![]() .
.
б) Знайти величину
кута між дотичними, проведеними в точках
перетину кривої
![]() з віссю
з віссю![]() .
Зробити креслення.
.
Зробити креслення.
Розв’язання. За аналогією з попереднім прикладом, знаходимо:
![]() (*)
(*)
Точки перетину
даної кривої із прямою
![]() знаходимо з розв’язку наступної системи:
знаходимо з розв’язку наступної системи:
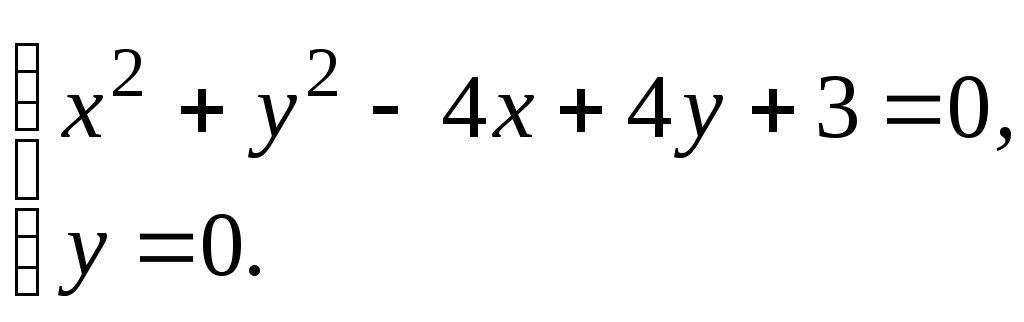
Таких точок дві:
![]() і
і![]() .
.
Враховуючи, що
![]() ,
,![]() ,
знаходимо згідно з (*) кутовий коефіцієнт
,
знаходимо згідно з (*) кутовий коефіцієнт![]() дотичної до даної кривої в точціА:
дотичної до даної кривої в точціА:
![]() .
.
Аналогічно знаходимо
кутовий коефіцієнт
![]() дотичної в точці В:
дотичної в точці В:
![]() .
.
Кут
![]() задовільняє рівності
задовільняє рівності![]() ,
отже
,
отже![]()
![]() ,
звідки
,
звідки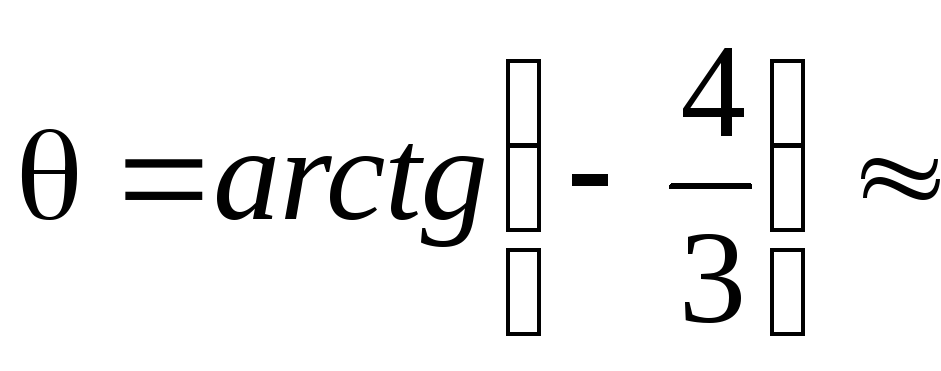 126055.
126055.
Перш ніж зробити
креслення, перетворимо початкове
рівняння кривої
![]() у рівняння
у рівняння![]() ,
що визначає коло із центром у точці
,
що визначає коло із центром у точці![]() та радіусом
та радіусом![]() (рис. 4.3).
(рис. 4.3).
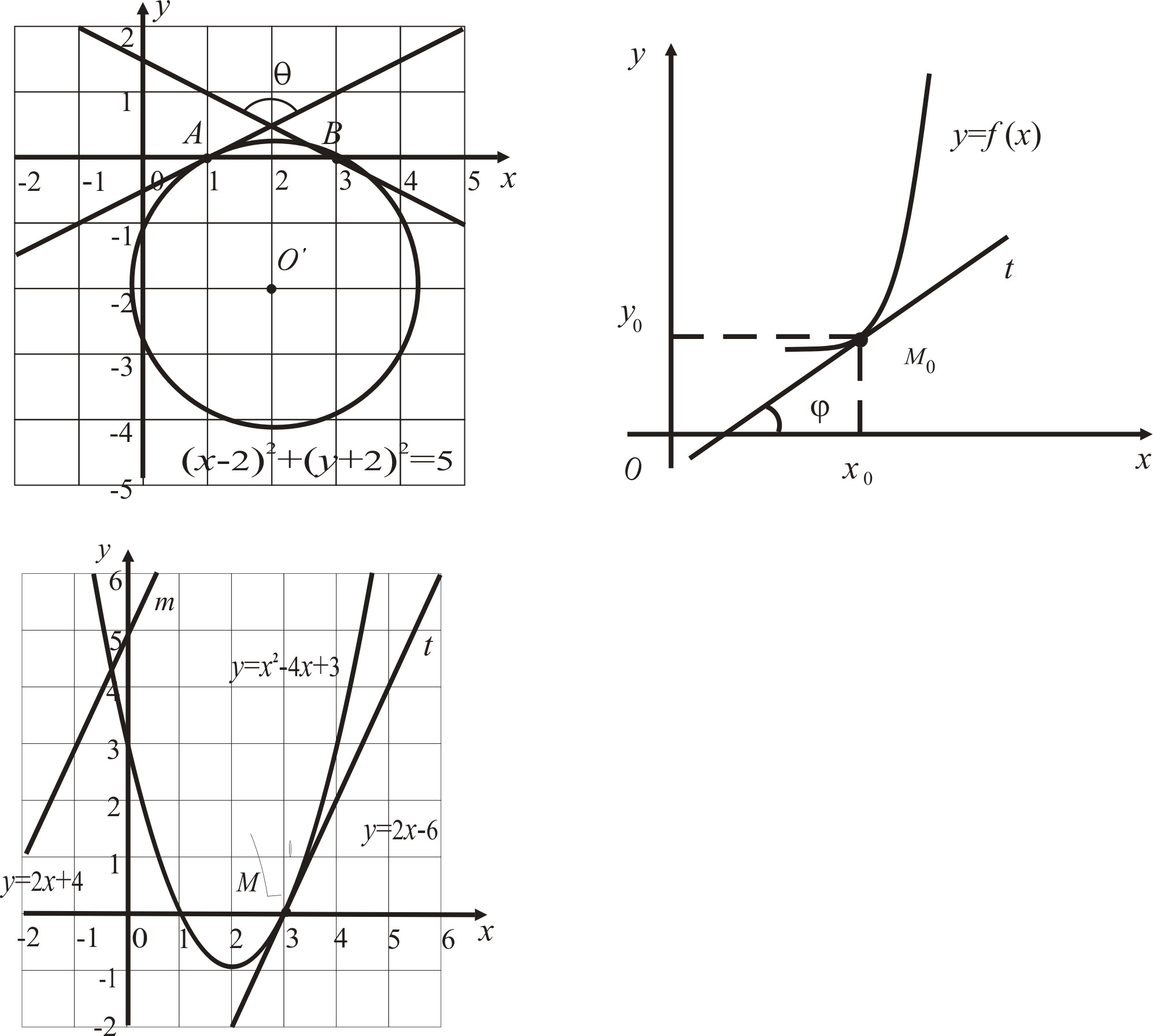
Рис. 4.3
Завдання
4.Знайти значення![]() у точці
у точці![]() для функцій, заданих неявно.
для функцій, заданих неявно.
|
|
5x2 + 3xy – 2y2 + 2 = 0 |
M (0; 1) |
|
|
x3 – 2x2 + y2 = 0 |
M (1; 1) |
|
|
x2 + xy + y2 = 7 |
M ( –1; –2) |
|
|
2x3 – xy + y – 2 = 0 |
M (1; 5) |
|
|
x3 + y3 – 3xy + 1 = 0 |
M ( –2;1) |
|
|
3x2 – xy + y – 3 = 0 |
M (1; –2) |
|
|
x2 + 2y2 + 6x – 4y – 13 = 0 |
M (1; –1) |
|
|
3x2 – 5y2 – 6x – 20y + 25 = 0 |
M (2; 1) |
|
|
4x2 + y2 + 8x – 4y + 3 = 0 |
M (0; 1) |
|
|
x3 – 2x2 y2 + 5x + y – 5 = 0 |
M (1; 1) |
|
|
2x2 – 9y2 + 4x + 18y + 11 = 0 |
M (2; –1) |
|
|
x3 – xy + y + 7 = 0 |
M ( –1; –3) |
|
|
x2 + y2 – 4x – 10y + 19 = 0 |
M (3; 2) |
|
|
x4 – y2 – y – 1 = 0 |
M (1; 0) |
|
|
x3 + 2xy2 + y + 11 = 0 |
M ( –1; –2) |
|
|
x3 + x2y + y2 – 13 = 0 |
M (1; 3) |
|
|
x3 + 5xy + y3 – 7 = 0 |
M (1; 1) |
|
|
x2 + 5xy + y2 – 2x + y – 6 = 0 |
M (1; 1) |
|
|
3x2 – xy + y3 – x = 0 |
M (0; 2) |
|
|
x 6 + y 6 – 2xy = 0 |
M(1; 1) |
|
|
x 2 +x2 y – y2 – y = 0 |
M (1; 1) |
|
|
x4 – 6x2y2 + 9y2 – 5x2 + 15y2 + 4 = 0 |
M (2; 1) |
|
|
7x2 + xy – y3 + 3 = 0 |
M (1; –2) |
|
|
x2y2 + xy + x2 – 7 = 0 |
M (1; 2) |
|
|
2x5 + y5 – 2xy + 26 = 0 |
M (1; –2) |
|
|
x5 + y5 – 2xy = 0 |
M (1; 1) |
|
|
3x2 – xy + y 2 + x – 34 = 0 |
M( –2; 4) |
|
|
x2 + 2xy2 + 3y4 – 6 = 0 |
M (1; –1) |
|
|
x2 – x2 y + y 2 = 13 |
M ( –1; –3) |
|
|
x2 y2 – 4y3 – x = 4 |
M (0; –1) |
Завдання
5.
Знайти величину кута між дотичними,
проведеними в точках перетину кривої![]() з віссю
з віссю![]() .
Зробити креслення.
.
Зробити креслення.
|
|
x 2+ y 2 + 2x + 2y –3 = 0. |
|
x 2 + y 2 – 2x + 4y –3 = 0. |
|
|
x 2 + y 2 + 10x + 9 = 0. |
|
x 2 + y 2 + 6x + 6y + 8 = 0. |
|
|
x 2 + y 2 + 4x + 2y + 3 = 0. |
|
x 2 + y 2 + 4x – 2y – 4 = 0. |
|
|
x 2 + y 2 + 6x – 6y + 8 = 0. |
|
x 2 + y 2 + 4x – 4y + 3 = 0. |
|
|
x 2 + y 2 + 6x + 2y + 1 = 0. |
|
x 2 + 6x + y 2 – 2y + 1 = 0. |
|
|
x 2 + 10x+ y 2 – 6y +16 = 0. |
|
x 2 + y 2 + 14x + 40 = 0. |
|
|
x 2 + y 2 – 6x – 2y + 6 = 0. |
|
x 2 + y 2 – 10 x+ 9 = 0. |
|
|
x 2 + y 2 + 10x + 6y + 16 = 0. |
|
x 2 + y 2 – 4x + 2y + 3 = 0. |
|
|
x 2 + y 2 – 2x + 4y – 20 = 0. |
|
x 2 + 6x + y 2 – 2y + 6 = 0. |
|
|
x 2 + y 2 – 4y – 4 = 0. |
|
x 2 – 6x + y 2 – 6y + 8 = 0. |
|
|
x 2 + y 2 – 14x + 40 = 0. |
|
x 2 + y 2 – 2x + 6y – 6 = 0. |
|
|
x 2 + y 2 – 6x + 6y + 8 = 0. |
|
x 2 + y 2 – 6x + 2y + 1 = 0. |
|
|
x 2 + 4x + y 2 – 2y + 3 = 0. |
|
x 2 + 4x + y 2 + 2y – 4 = 0. |
|
|
x 2 + y 2 + 4x – 4 = 0. |
|
x 2 + y 2 + 2x – 2y – 4 = 0. |
|
|
x 2 + 4x + y 2 – 2y – 3 = 0. |
|
x 2 + y 2 + 2x + 4y – 4 = 0. |
