2. Геометричне застосування похідної
2.1. Теорема.Якщо крива задана рівнянням
,
то значення
похідної
у точці
дорівнює кутовому коефіцієнту
дотичної до графіка функції
,
проведеної в точці
:
,
де
(рис. 2.1).
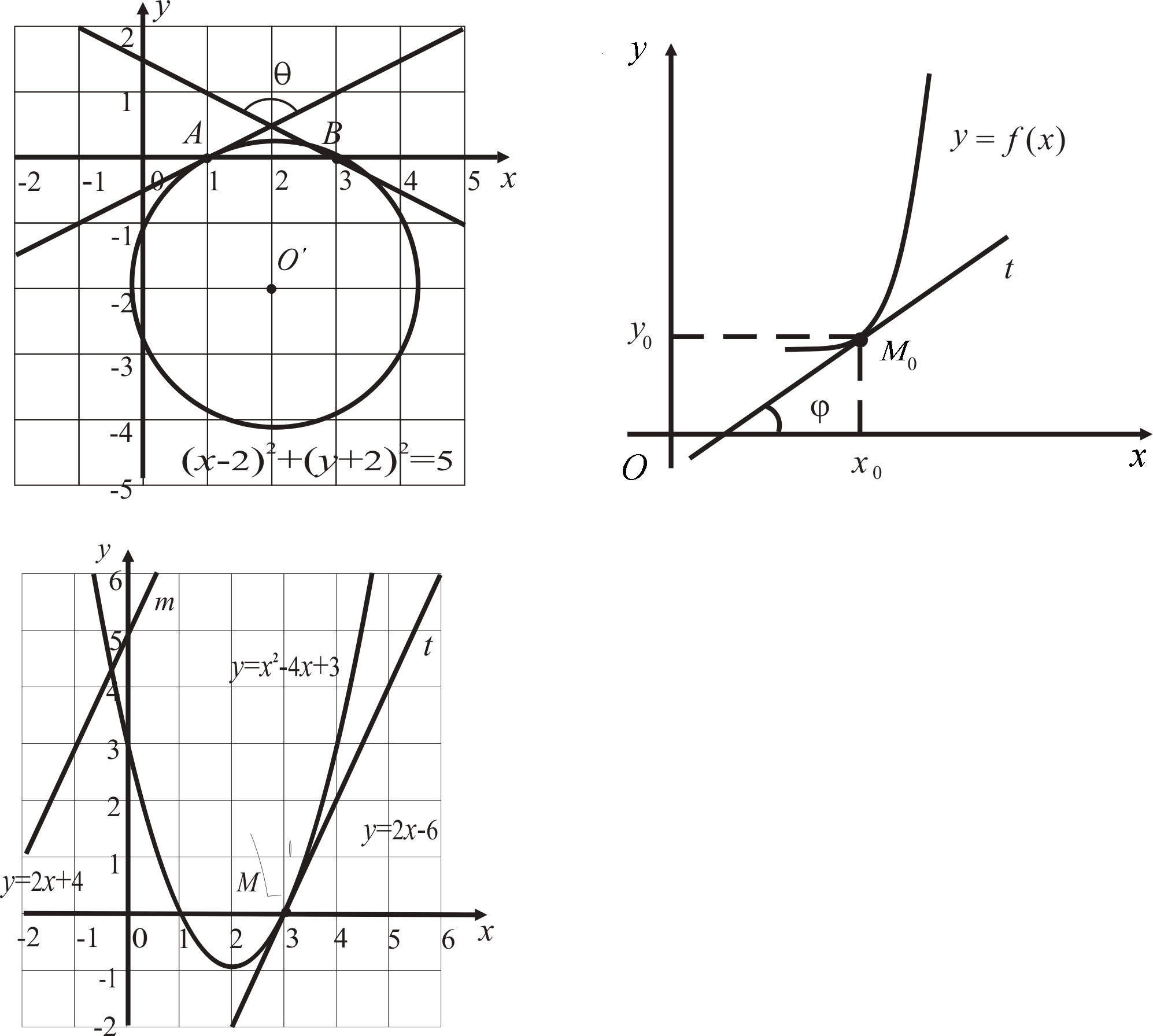
Рис. 2.1
2.2. Рівняння
дотичної до кривої
у точці
має вигляд:
або
.
2.3. Кутом між двома кривими в точці їх перетинуназивається кут між дотичними до кривих у цій точці.
Кут
між двома прямими з кутовими коефіцієнтами
та
відповідно визначається за формулою
,
причому знак “плюс” відповідає гострому
куту
,
а знак “мінус” – тупому.
Якщо
,
то дотичні – взаємно перпендикулярні,
а криві називаються ортогональними.
2.4. Приклад.Знайти рівняння дотичної до графіка
функції
,
яка паралельна прямій
.
Зробити креслення.
Розв’язання.
Графік функції
– парабола. Так як
при
,
,
то вершиною параболи є точка з координатами
(2; –1). За умовою, дотична
до параболи і дана пряма
з рівнянням
паралельні; отже, їх кутові коефіцієнти
рівні:
,
,
.
Отже,
– абсциса точки дотику
параболи та прямої
,
– її ордината. Таким чином, рівняння
дотичної
має вигляд:
(рис. 2.2).
Рис. 2.2
Завдання
2.Знайти рівняння дотичної до графіка
функції
,
яка проходить паралельно прямій
.
Зробити креслення.
|
|
|
|
|
|
|
|
|
y = x2 – 6x + 8, |
y = 6x + 1 |
|
y = – x2 – 2x + 3, |
y = – 2x – 2 |
|
|
y = x2 – 6x + 8, |
y = 2x + 3 |
|
y = x2– 2x – 3, |
y = – 4x +2 |
|
|
y = x2 – 2x –3, |
y = 6x + 3 |
|
y = x2 + 2x – 3, |
y = 2x – 2 |
|
|
y = x2 + 8x – 9, |
y = 2x + 1 |
|
y = x2 – 4x + 3, |
y = 2x + 4 |
|
|
y = x2 – 5x + 4, |
y = – x – 2 |
|
y = x2 + 2x – 3, |
y = 4x – 1 |
|
|
y = – x2 – 2x +3, |
y = – 6x + 4 |
|
y = x2 + 8x – 9, |
y = 4x |
|
|
y = x2 – 5x + 4, |
y = x + 3 |
|
y = x2 – 2x – 3, |
y = 4x –1 |
|
|
y = x2 – 6x + 8, |
y = – 4x + 2 |
|
y = – x2 – 2x + 3, |
y = 4x –3 |
|
|
y = x2 + x, |
y = x – 3 |
|
y = – x2 – 2x + 3, |
y = 2x + 1 |
|
|
y = x2 + 8x – 9, |
y = 6x |
|
y = x2 – 8x – 9, |
y = – 6x |
|
|
y = – x2 + 4x, |
y = 2x |
|
y = x2 – 5x + 4, |
y = – 3x – 1 |
|
|
y = x2 + 8x – 9, |
y = – 2x + 1 |
|
y = x2 – 4x + 3, |
y = 4x + 4 |
|
|
y = x2 – 2x – 3, |
y = 2x + 2 |
|
y = x2 + 2x – 3, |
y = – 4x + 2 |
|
|
y = x2 – 6x + 8, |
y = 4x + 1 |
|
y = x2 –5x + 4, |
y = 3x + 1 |
|
|
y = x2 – 4x + 3, |
y = 6x – 6 |
|
y = x2 – 4x + 3, |
y= – 4x – 4 |
