Динамика билеты / 5Первая задача динамики
.docx
![]()
 или
или

 или
или
 где
где ![]() –
проекции ускорения
–
проекции ускорения ![]() на
естественные оси координат;
на
естественные оси координат; ![]() –
дуговая координата точки;
–
дуговая координата точки; ![]() –
скорость точки;
–
скорость точки; ![]() –
радиус кривизны траектории;
–
радиус кривизны траектории; ![]() –
проекции силы
–
проекции силы ![]() на
естественные оси координат.
на
естественные оси координат.

![]()
Первая задача динамики свободной точки
Первой или прямой называется задача, в которой заданы масса точки и закон ее движения в декартовых координатах или в естественной форме. Необходимо определить модуль и направление силы, действующей на точку.
Для решения задачи надо выполнить следующие операции:
– построить расчетную схему, на которой в соответствии с условием задачи изобразить систему осей координат, нарисовать траекторию точки и отметить на траектории то положение точки, для которого требуется найти действующую силу. Эту силу следует представить составляющими на выбранные оси координат;
– по заданному движению материальной точки определить проекции ее ускорения на принятые оси координат;
– составить дифференциальные уравнения движения материальной точки в форме (1.2) или (1.3) и из полученных уравнений определить проекции искомой силы, а затем ее модуль и направляющие косинусы.
Задача
1.1. Материальная точка массой 10
кг совершает движение в горизонтальной
плоскости согласно уравнениям ![]()
![]() где
где ![]() –
в метрах;
–
в метрах; ![]() –
в секундах. Определить силу
–
в секундах. Определить силу ![]() ,
действующую на точку в момент
,
действующую на точку в момент ![]() .
.
|
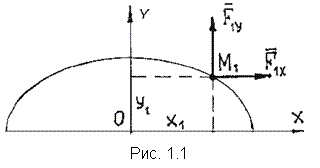
Решение Построим расчетную схему. В соответствии с условием задачи принимаем декартовые оси координат (рис 1.1). Из заданных уравнений движения следует, что траекторией точки является эллипс (на рис 1.1 – половина эллипса). Положение точки в
момент
|
|
Искомую
силу представим ее составляющими ![]() .
Вычислим проекции ускорения точки на
оси координат:
.
Вычислим проекции ускорения точки на
оси координат:
![]() .
.
Для заданного
момента ![]() имеем:
имеем:
![]() .
.
Из дифференциальных уравнений (1.2) находим:
![]() .
.
Затем
определяем модуль силы ![]() и
направляющие косинусы
и
направляющие косинусы
 .
.