Динамика билеты / 22Внешние и внутренние силы. Главный вектор, момент. Работа

Внешние силы - это такие силы, которые действуют только на поверхность предмета, но не проникают внутрь его. К этим силам относятся все силы, развиваемые материальным объектом.

Внутренние силы - это такие силы, которые действуют сразу на все атомы передвигаемого предмета независимо от того, где они находятся: на поверхности или в середине предмета. К этим силам относятся силы инерции и силы поля: гравитационного, электрического, магнитного. И происходит это потому, что поле и носитель инерции физвакуум свободно проникают внутрь любого тела.

В механике внешними силами по отношению к данной системе материальных точек (т. е. такой совокупности материальных точек, в которой движение каждой точки зависит от положений или движений всех остальных точек) называются те силы, к-рые представляют собою действие на эту систему других тел (других систем материальных точек), не включенных нами в состав данной системы.

Внутренними силами являются силы взаимодействия между отдельными материальными точками данной системы. Подразделение сил на внешние и внутренние является совершенно условным: при изменении заданного состава системы некоторые силы, ранее бывшие внешними, могут стать внутренними, и обратно. Так, например, при рассмотрении

PRIMER движения системы, состоящей из земли и ее спутника луны, силы взаимодействия между этими телами будут внутренними силами для этой системы, а силы притяжения солнца, остальных планет, их спутников и всех звезд будут внешними силами по отношению к указанной системе. Но если изменить состав системы и рассматривать движение солнца и всех планет как движениеодной общей системы, то внешн. силами будут только силы притяжений, оказываемых

Если нагруженное тело находится в равновесии, то внутренние силы равны по значению внешним силам и противоположны им по направлению. Очевидно, что они препятствуют развитию деформации.Работа внутренних сил (U), с учетом их направления по отношению к деформации, всегда является отрицательной.

Работа внешних сил равна взятой с обратным знаком работе внутренних сил:

.

Пусть элемент стержня длиной испытывает растяжение (рис. 15.3, а).

Действие отброшенных частей стержня на рассматриваемый элемент заменим продольными силами N. Эти усилия показаны на рисунке штриховыми линиями. По отношению к элементу они являются как бы внешними. Вызываемое ими удлинение элемента равно: .

 Действие рассматриваемого элемента на отброшенные части показано на рисунке сплошными линиями. Элементарная работа внутренних продольных сил, постепенно увеличивающихся, и противодействующих развитию удлинения, согласно теореме Клапейрона, выразится формулой: .

ЭЛЕМЕНТАРНАЯ РАБОТА ВНУТРЕННИХ ПОПЕРЕЧНЫХ СИЛ () ПРИ ЧИСТОМ СДВИГЕ (РИС. 15.3, Б)

При чистом сдвиге касательные напряжения равномерно распределены по всему сечению и определяются по формуле: .

Абсолютный сдвиг правого сечения элемента по отношению к левому сечению, с учетом закона Гука, равен: ,

тогда .

При поперечном изгибе касательные напряжения распределены по сечению неравномерно. В этом случае выражение для элементарной работы внутренних перерезывающих сил может быть представлено в виде: , где k – коэффициент, зависящий от формы поперечного сечения стержня. Например, для прямоугольного поперечного сечения .

ЭЛЕМЕНТАРНАЯ РАБОТА ВНУТРЕННИХ УСИЛИЙ ПРИ КРУЧЕНИИ

Поворот правого сечения элемента по отношению к левому сечению, происходящий под действием внешних по отношению к нему крутящих моментов (), показанных (см. рис. 15.3, в) штриховыми линиями, равен: .

Тогда работа внутренних крутящих моментов (они на рисунке не показаны) на этом угле поворота определяется по формуле: .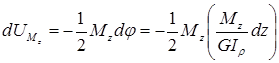

Пусть теперь элемент стержня испытывает изгиб. И пусть его правое поперечное сечение повернется на угол поворота по отношению к левому сечению (см. рис. 15.3, г).

Тогда внутренние изгибающие моменты, показанные (см. рис. 15.3, г) сплошными линиями, совершат на этом угле поворота работу:

.

При одновременном растяжении, кручении и прямом поперечном изгибе стержня (с учетом того, что работа каждого из внутренних усилий на перемещениях, вызываемых остальными усилиями, равна нулю) получим следующее выражение для элементарной работы внутренних сил упругости:

.

Интегрируя выражение по всей длине стержня, окончательно получим формулу работы внутренних сил:

.