
двойные интегралы
.pdf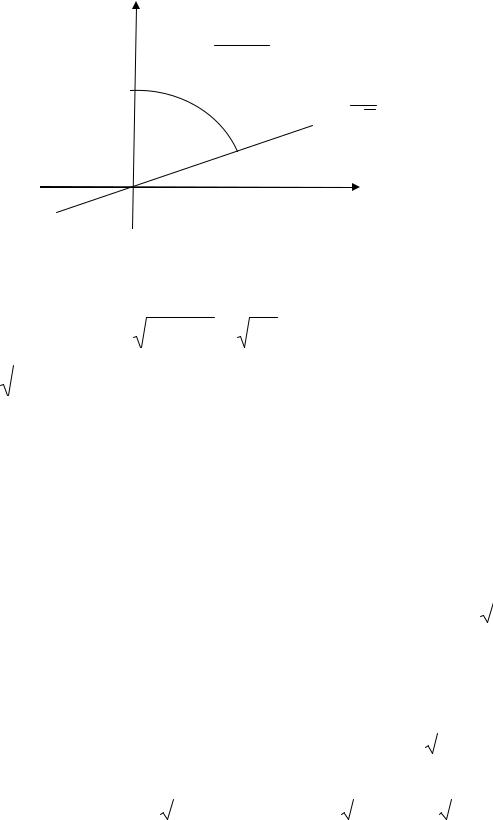
y
x 
 4 y2
4 y2
y 1 x

 3
3
x
Рис.6.5
3) Представим интеграл повторным согласно формуле (4.3). Для этого выпишем подынтегральную функцию и преобразуем ее в полярную систему
координат согласно (4.2) |
x2 y2 |
|
2 . Тогда: |
||
|
|
dxdy |
d d d 2d |
||
|
x2 y2 |
||||
Sxy |
|
|
S |
|
|
4) Для расстановки пределов интегрирования в повторном интеграле обратимся к заданной области (рис.6.5). Проведем стрелки радиус вектора из начала координат через указанную область. Получаем, что переменная изменяется от начала координат до радиуса окружности 2, т.е.
0 2. Угол |
будет изменяться от уравнения прямой |
y |
1 |
|
x до |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
3 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
положительного направления оси Oy, т.е. до |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
. Чтобы определить угол |
||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
наклона прямой, достаточно подставить в ее уравнение y |
1 |
|
|
|
x полярные |
|||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||
координаты (4.1): |
sin |
1 |
cos , |
sin |
|
1 |
|
, tg |
|
1 |
, |
|
|
. |
||||||||||||||||||||
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
3 |
|
6 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Т.е. |
|
|
|
|
. |
Окончательно получаем: d 2d . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

5) Вычислим полученный интеграл поочередно.
2 |
|
3 |
|
2 |
|
8 |
|
|
|
|
|
||||||
2d |
|
|
|
|
|
. |
||
3 |
|
|
|
|
||||
0 |
|
|
0 |
3 |
||||
|
|
|
|
|
|
|||
Полученный результат подставляем в интеграл по d и вычисляем его:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 8 |
8 |
|
8 |
|
|
|
|
|
16 |
||||||||||
|
|
|
|
|
|||||||||||||||
|
2 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|||||||||||||
|
3 |
3 |
|
|
3 |
|
2 |
6 |
|
|
9 |
|
|||||||
|
|
||||||||||||||||||
|
|
6 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
16 |
|
|||
|
x2 y2 |
|
|
|||||
Окончательно имеем: |
dxdy d 2d |
|
. |
|||||
9 |
||||||||
S |
|
|
0 |
|
||||
|
|
|
6 |
|
|
|
|
|
7.Приложение двойного интеграла
1.Площадь плоской фигуры, ограниченной областью D:
S dxdy |
(7.1) |
D |
|
2. Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z f (x, y), снизу плоскостью z 0 и сбоку цилиндрической поверхностью, вырезающей на плоскости xOy область D:
V f (x, y)dxdy |
|
|
|
|
(7.2) |
|||||
|
D |
|
|
|
|
|
|
|
|
|
3. Если гладкая поверхность задана |
уравнением |
z f (x, y), то |
||||||||
площадь поверхности выражается формулой: |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
z 2 |
|
z |
2 |
|
|
||
S |
|
1 |
|
|
|
|
|
dxdy |
(7.3) |
|
|
|
|||||||||
|
|
x |
|
|
|
|
|
|
||
|
D |
|
y |
|
|
|
||||
где D – проекция данной поверхности на плоскость xOy.
22
4. Если пластинка занимает область D плоскости xOy и имеет
переменную поверхностную плотность (x, |
y), то масса M пластины |
|||||||||
выражается двойным интегралом: |
|
|
|
|
|
|
||||
|
|
|
M (x, y)dxdy |
(7.4) |
||||||
|
|
|
|
D |
|
|
|
|
|
|
5. Статические моменты пластины относительно осей Ox и Oy |
||||||||||
находятся по формулам: |
|
|
|
|
|
|
|
|
||
Mx y (x, y)dxdy, M y |
x (x, |
y)dxdy |
(7.5) |
|||||||
D |
|
|
D |
|
|
|||||
6. Координаты центра тяжести пластины вычисляются по |
||||||||||
формулам: |
|
|
|
|
|
|
|
|
||
|
|
|
M y |
|
|
|
Mx |
|
|
|
x |
y |
|
|
|||||||
|
, |
|
|
(7.6) |
||||||
|
M |
|
||||||||
|
|
|
M |
|
|
|
|
|
||
где M – масса пластины, а Mx, M y – ее статические моменты относительно осей координат.
7. Моменты инерции пластины относительно осей Ox и Oy
вычисляются по формулам:
Ix y2 |
(x, y)dxdy, Iy x2 (x, y)dxdy |
(7.7) |
D |
D |
|
8. Момент инерции относительно начала координат – по формуле: |
|
|
|
I0 (x2 y2) (x, y)dxdy Ix Iy |
(7.8) |
|
D |
|
23

8.Дополнительные задания
1)Вычислить объем тела ограниченного заданными поверхностями:
x y z 1, y2 x, x 1, y 0,z 0.
2)Найти площадь части поверхности цилиндра z x2, вырезанной плоскостями x y 
 2, x 0, y 0.
2, x 0, y 0.
3)Определить центр тяжести полусегмента параболы y2 2x,
отсеченного прямыми x 2, y 0.
4)Найти центр тяжести площади, ограниченной параболами y2 x и
x2 y.
5)Вычислить массу круглой пластины радиуса r 3, если плотность ее обратно пропорциональна расстоянию точки от центра и равна на краю пластины.
24
Список литературы
1.Письменный Д.Т., Конспект лекций по высшей математике: полный курс. 7-е изд.- М.: Айрис-пресс. 2008. – 608с.
2.Выгодский М.Я., Справочник по высшей математике. М.: ООО
«Издательство Артель»: ООО «Издательство АСТ», 2004. – 991с.
3.Рябушко А.П. и др., Индивидуальные задания по высшей математике.
Часть 3, Изд-во: Минск: Вышейшая школа, 2006. – 338с.
Математические веб-сайты:
MathWorld: Wolfram Web Resource by Eric W. Weisstein, один из самых больших веб-сайтов по математике
Mathematical Atlas by Dave Rusin, один из самых больших веб-сайтов по математике
PlanetMath.Org – Математическая энциклопедия
Общие директории, содержащие информацию о математических сайтах
Google: Mathematics Web Sites, содержит обширную информацию о различных математических веб-сайтах
Yahoo: Mathematics Web Sites, содержит обширную информацию о различных математических веб-сайтах
Math Forum: Internet Mathematics Library, содержит обширную информацию о различных математических веб-сайтах
Mathematical WWW Virtual Library (Florida State University), содержит обширную информацию о различных математических веб-сайтах
Internet Guide to Engineering, Mathematics and Computing, содержит обширную информацию о различных математических веб-сайтах
Mathematics Web Sites (Pennsylvania State University), содержит обширную информацию о различных математических веб-сайтах
MathGuide (SUB Gottingen), содержит полезную информацию о различных математических веб-сайтах
Math-Net (International Mathematical Union), содержит полезную информацию о различных математических веб-сайтах
25
|
Оглавление |
|
1. |
Двойной интеграл в декартовой системе координат |
...................................................3 |
2. |
Практикум...................................................................................................................... |
5 |
3. |
Решение типового варианта.......................................................................................... |
6 |
4. |
Двойной интеграл в полярной системе координат.................................................... |
11 |
5. |
Практикум.................................................................................................................... |
12 |
6. |
Решение типового варианта........................................................................................ |
15 |
7. |
Приложение двойного интеграла ............................................................................... |
22 |
8. |
Дополнительные задания............................................................................................ |
24 |
Список литературы................................................................................................................. |
25 |
|
26
ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ
Методические указания Составители: Дегтярева Н.Е.
Корректор:
Технический редактор
Подписано в печать . Формат
Печать офсетная. Усл.печ.л. Уч.-изд.л.
Тираж 60 экз. Заказ
_____________________________________________________________
Издательство ДВФУ.690650, Владивосток, Пушкинская, 10
Типография издательства ДВФУ, 690650, Владивосток,
Пушкинская, 10
27
