
3. Обратная матрица
.doc
3. ОБРАТНАЯ МАТРИЦА
Присоединенная матрица
3.1. Что такое присоединенная (союзная) матрица?
3.2. Найдите присоединенные матрицы для следующих матриц:
а)
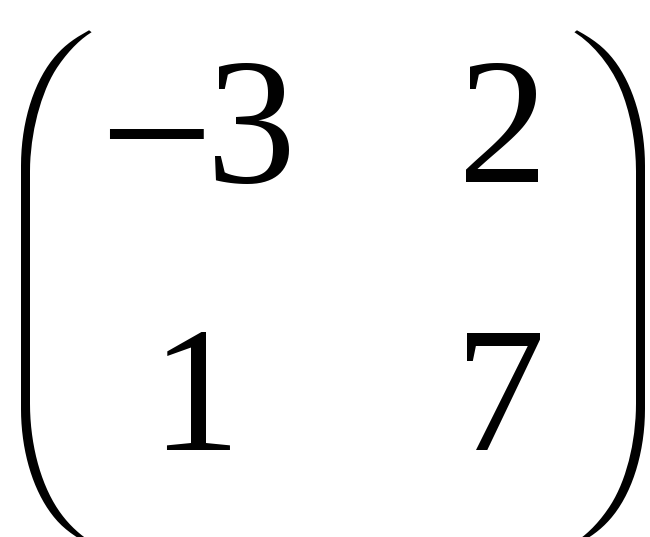 ;
б)
;
б)
 .
.
3.3. Сформулируйте утверждение о произведении матрицы на свою присоединенную. Проследите (по конспекту) его доказательство.
3.4. Найдите произведения матриц из задания 3.2 (а, б) на их присоединенные.
Существование и единственность обратной матрицы.
3.5. В каком случае квадратную матрицу называют невырожденной (вырожденной)? Приведите примеры.
3.6. Сформулируйте определение обратной матрицы.
3.7. Пользуясь определением обратной матрицы, проверьте, являются ли следующие матрицы взаимно обратными:
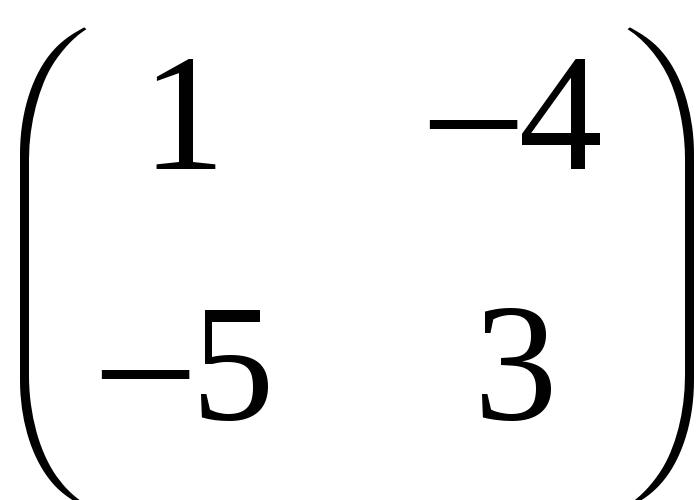 и
и
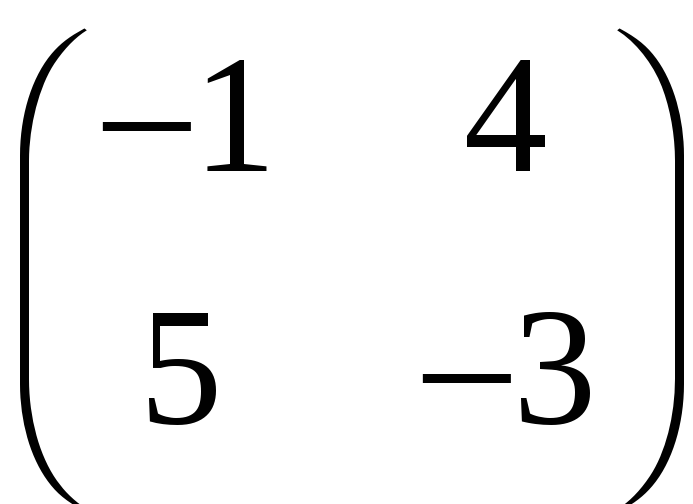 .
.
3.8. Сформулируйте теорему о существовании обратной матрицы. Проследите (по конспекту) ее доказательство (необходимость и достаточность).
3.9. Сформулируйте и проследите доказательство утверждения о единственности обратной матрицы (по конспекту).
3.10*. Докажите следующие свойства операции перехода к обратной матрице:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
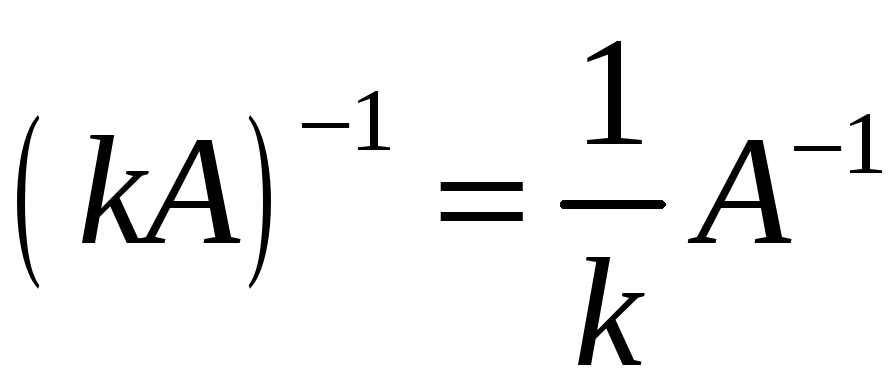 ,
,
![]() ;
5)
;
5)
![]() ,
,
![]() ;
;
6)
![]() ;
7)
;
7)
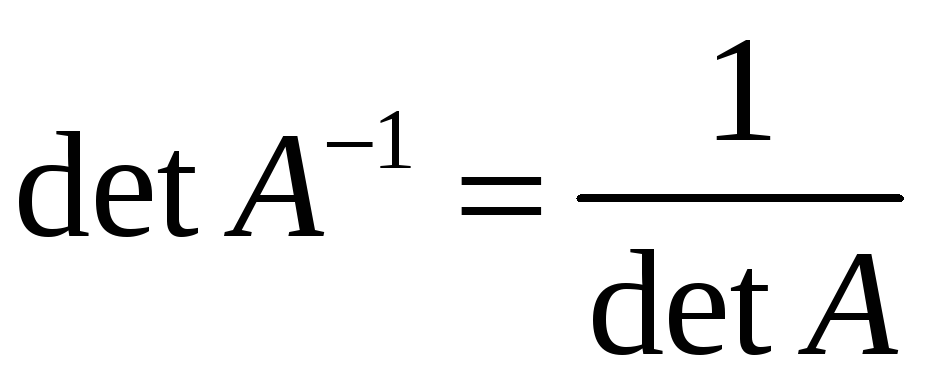 .
.
Нахождение обратной матрицы
3.11. Выпишите формулу для нахождения обратной матрицы. Пользуясь этой формулой, найдите обратные следующих матриц и сделайте проверку правильности нахождения:
а)
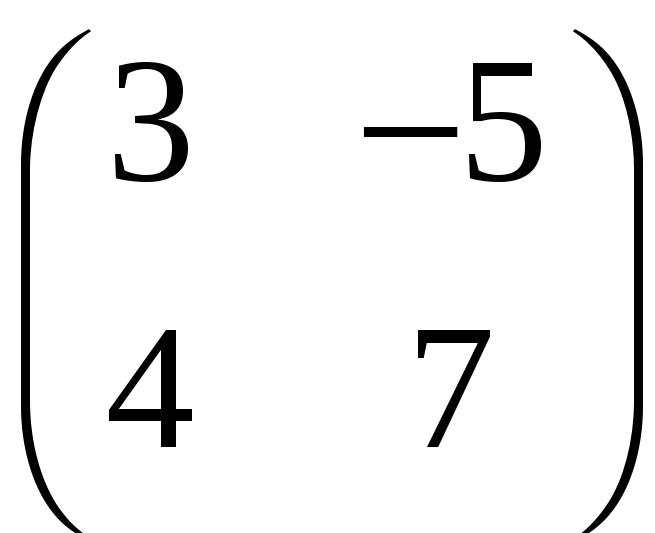 ;
б)
;
б)
 ;
в)
;
в)
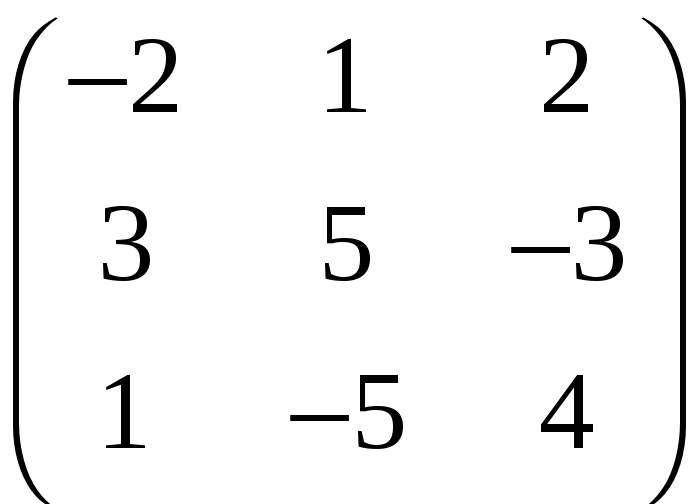 ;
г)
;
г)
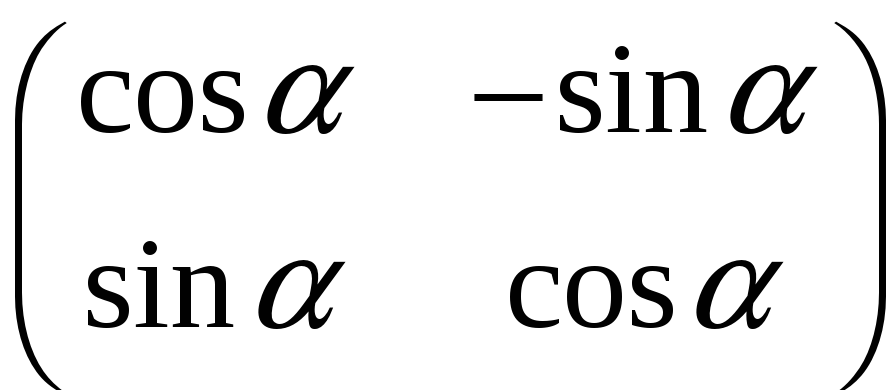 ;
;
д)
 .
.
3.12*. Какие действия над строками матрицы называют элементарными преобразованиями?
3.13*. В чем заключается метод элементарных преобразований нахождения обратной матрицы?
3.14*. Для следующих матриц найдите обратные методом элементарных преобразований. Сделайте проверку:
а)
3.15. Решите матричные уравнения:
а)
 ;
б)
;
б)
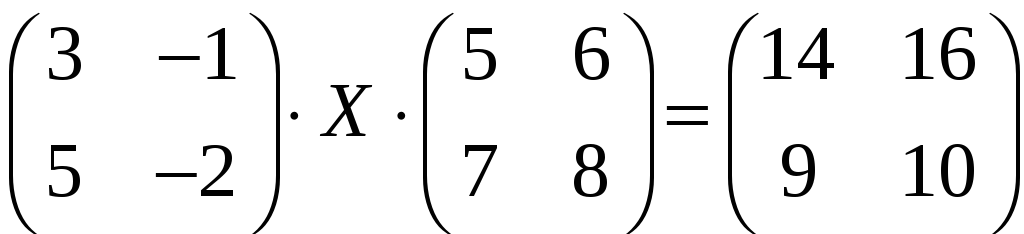
в)
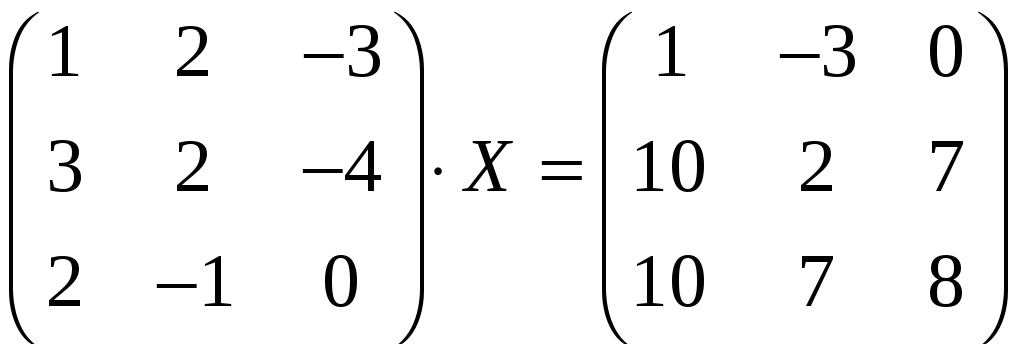 .
.
