Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы

Метод Гаусса-Зейделя

При решении задач САПР чаще всего приходится иметь дело с математическими моделями, в которых нет аналитических зависимостей для первых производных минимизируемой функции (). Поэтому поиск локального минимума в этом случае приходится вести по результатам вычислений только значений функции() – с помощьюпрямых методов оптимизации.

Рассматривается следующая многомерная задача безусловной оптимизации (точнее говоря, задача многомерной локальной безусловной оптимизации): найти минимум критерия оптимальности (), определенного в-мерном евклидовом пространстве,

(1)

При решении задачи (1) методом Гаусса-Зейделя (методом покоординатного спуска, методом циклического покоординатного спуска) используются следующие итерационные формулы

(2)

где вектор определяет направление вдоль-й координатной оси и представляет собой-мерный вектор с компонентами

а величины ,,...,– определяются из условий

(3)

Другими словами, величина ,представляет собой длину шага, минимизирующего функциюв направлениина итерации номер, исходя из точки, полученной на предыдущем шаге.

Если положить =,=, то формулы (2), (3) можно записать в виде

(4)

(5)

Таким образом, каждая итерация по методу Гаусса-Зейделя включает в себя шагов. Каждая последующая итерация начинается из точки, полученной на последнем шаге предыдущей итерации. Поиск заканчивается при выполнении одного изстандартных условий окончания итераций:

(6)

Заметим, что задачи (5) даже в случае одноэкстремальной функции () могут бытьзадачами многоэкстремальной оптимизации и могут быть решены рассмотренными в главе 4 методами решения задач одномерной оптимизации.

Схема метода Гаусса-Зейделя:

1. Задаем начальную точку и полагаем=0 ,=1.

2. Последовательно для =1,2,...,решаем задачи (5), т.е. исходя из предыдущей точки, отыскиваем минимум функции() вдоль-го координатного направления;

3. Если условие окончания поиска (6) или (6') выполнено, то полагаем и заканчиваем вычисления. Иначе - полагаем=+1 и переходим к п. 2

Метод Гаусса-Зейделя иллюстрирует рис. 1, на котором показан фрагмент линий уровня функции Химмельблау . На рис. 1 точкапредставляет собой локальный минимум функции() вдоль оси X₁ при исходной точке . Точкапредставляет собой локальный минимум функции() вдоль оси X₂ при исходной точке . Отыскание точкизавершает первую итерацию. Следующая итерация начинается из точки=. И т.д.

Линии уровня на рис. 1 получены с помощью следующей MATLAB-программы:

x=-6:0.05:0;

y=x;

[X,Y]=meshgrid(x);

Z=(X.^2+Y-11).^2+(X+Y.^2-7).^2;

V=[1,4,8,16,32,64,100,150,200,250];

contour(X,Y,Z,V);

Рис. 1.  Траектория поиска минимума не овражной функции Химмельблау методом Гаусса-Зейделя.

Метод Гаусса-Зейделя медленно сходится на овражных функциях, в которых овраг не ориентирован в направлении какой-либо из координатных осей (см. рис. 2). На рисунке показаны линии уровня функции Розенброка (=2). Линии уровня получены с помощью следующей MATLAB-программы:

x=-2:0.06:2;

y=x;

[X,Y]=meshgrid(x);

Z=100.*(Y-X.^2).^2+(1-X).^2;

V=[1,5,50,500];

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

Рис. 2.  Траектория поиска минимума овражной функции Розенброка методом Гаусса-Зейделя. Текущая точка быстро (в данном случае – за один шаг) «скатывается» на дно оврага и очень медленно движется по дну оврага к минимуму функции Ф(Х).

Метод Гаусса-Зейделя. Тест 1

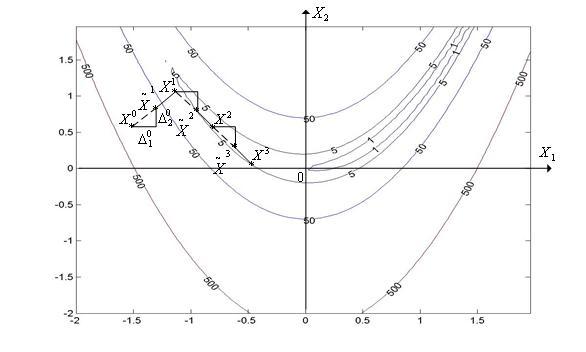
Выполните несколько итераций (не менее двух) решения двумерной локальной задачи безусловной оптимизации

(1)

(2)

методом Гаусса-Зейделя, исходя из точки =(,)=(-1.5,1.5).

Траекторию поиска изобразите на рисунке, содержащем линии уровня квадратичной функции (2), которые можно получить с помощью следующей MATLAB-программы:

x=-2:0.06:2;

y=x;

[X,Y]=meshgrid(x);

Z=(X).^2+(Y).^2+3*(X+Y).^2;

V=[0.1,0.2,0.4,0.8,1.5,3.,6.,12,24];

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

 Ответ 

Итерационная формула Гаусса-Зейделя.

Каждая итерация метода Гаусса-Зейделя для задачи (1), (2) состоит из двух шагов и имеет вид

(3)

(4)

где величины ,– определяются из условий

(5)

(6)

Найдем явное решение задачи (5). Из (5) имеем

(7)

Функция (7) относительно является квадратичной функций с положительным коэффициентом прии достигает минимума в точке, удовлетворяющей условию

из которого имеем

(8)

Аналогично явное решение задачи (6) равно

(9)

Таким образом, из (3), (4), (8), (9) имеем искомую итерационную формулу метода Гаусса-Зейделя для задачи (1), (2)

(10)

(11)

Первая итерация (=1).

Из формул (10) имеем иАналогично из формул (11) имеемТаким образом,(см. рис. 1).

Вторая итерация (=2).

Аналогично первой итерации, имеем

,

Таким образом, (см. рис. 1).

Рис. 1.  Фрагмент (две итерации) траектории поиска минимума функции (2) методом Гаусса-Зейделя, исходя из точки X⁰=(x⁰,y⁰)=(-1.5,1.5).

Метод Хука-Дживса

Рассмотрим следующую многомерную задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в-мерном евклидовом пространстве,

(1)

При решении задачи (1) методом Хука-Дживса (методом конфигураций, методом пробных шагов) используются итерационные формулы, аналогичные формулам, используемым в методе Гаусса-Зейделя

(2)

где принято ,, векторопределяет направление вдоль-й координатной оси и представляет собой-мерный вектор с компонентами

величины ,,...,– определяются из условий

(3)

После завершения шагов выполняется спуск в направлении вектора (-) по формуле

(4)

где - ускоряющий множитель. В различных модификацияхметода Хука-Дживса множитель может

• приниматься постоянным (обычно, равным 2),

• выбираться из условия ()<(),

• находиться из условия локального минимума функции () при движении из точкив направлении вектора:

(5)

Заметим, что задачи (5) даже в случае одноэкстремальной функции () могут бытьмногоэкстремальными задачами оптимизации и могут быть решены рассмотренными в главе 4 методами решения задач одномерной оптимизации.

Итерации заканчиваются при выполнении одного из стандартных условий окончания итераций:

(6)

Вектор является вектором свободных параметров метода - вектором «пробных шагов» по всемкоординатным осям.

Известна модификация метода Хука-Дживса, в которой точка определяется не процедурами (2), (3), аметодом Гаусса-Зейделя.

Схема метода Хука-Дживса:

1. Задаем начальную точку , вектор «пробных» шагови полагаем=0.

2. Последовательно для =1,2,...по формулам (2), (3) находим точки.

3. Если , то переходим к п. 4). Иначе уменьшаем длины «пробных» шагов, например, вдвое и переходим к п.2).

4. Если условие окончания поиска (6) или (6') выполнено, то полагаем и заканчиваем вычисления. Иначе выполняем спуск в направлении векторапо формуле (4), в которой ускоряющий множитель находится, например, из условия (5). Полагаеми переходим к п. 2

Метод Хука-Дживса иллюстрирует рис. 1, на котором показаны линии уровня функции Химмельблау (=2). Ускоряющий множительнаходиться из условия локального минимума функции() при движении из точкив направлении вектора.

Рис. 1.  Траектория поиска минимума не овражной функции Химмельблау методом Хука-Дживса.

Метод Хука-Дживса имеет высокую эффективность в случае, если функция () имеет прямолинейный овраг (не обязательно ориентированный вдоль одного из координатных направлений, как вметоде Гаусса-Зейделя). При минимизации "овражных" функций, имеющих не прямолинейный овраг, процесс поиска может сильно замедлиться и закончиться далеко от точки истинного минимума (см. рис. 2). На рисунке показаны линии уровня функции Розенброка (=2).

Рис. 2.  Траектория поиска минимума овражной функции Розенброка методом Хука-Дживса. Ускоряющий множитель α^r принят равным двум.

Метод Розенброка

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в-мерном евклидовом пространстве,

(1)

Ортогонализация Грамма-Шмидта.

При решении задачи (1) методом Розенброка (методом вращающихся координат) используется преобразование на каждой итерации системы координат таким образом, чтобы в новой системе координат одна из осей совпадала с направлением предыдущего шага. Остальные оси новой системы координат обычно находят с помощью процедуры ортогонализации Грамма-Шмидта.

Рассмотрим произвольный набор векторов пространства. Поставим задачу построить на основе этих векторов ортонормированный набор векторовтого же пространства.

Напомним, что набор векторов называется ортонормированным, если для любых двух векторов из этого набора выполняется условие

(2)

Или, другими словами, набор векторов ортонормирован, если эти векторы линейно независимы и скалярное произведение любых двух из них равно единице.

Для построения векторов применим индуктивный подход. Положим, что

(3)

где - символ евклидовой нормы. Полагая векторыуже построенными будем искать векторв виде

(4)

Для отыскания неизвестных множителей умножим (4) скалярно на вектор:

Поскольку , имеем

(5)

Множитель найдем из условия:

(6)

Определение 1. Процесс перехода от векторов к векторамсогласно формулам (3) – (6) называется ортогонализацией Грамма-Шмидта

Схема метода Розенброка.

Каждая итерация метода Розенброка состоит из двух этапов. В зависимости от модификации метода первый этап может выполняться с использованием различных методов. Рассмотрим применение на первом этапе итерационной формулы метода Гаусса-Зейделя. Приведем формулировку этой формулы, несколько отличную от формулировки, рассмотренной в параграфе 6.1.

Положим ,и пусть- орты системы координат, используемой на-ой итерации. Тогда итерационную формулуметода Гаусса-Зейделя можно записать в виде

(7)

где коэффициенты находятся из условий

(8)

На втором этапе каждой из итераций система векторов с использованием ортогонализации Грамма-Шмидта заменяется новой системой линейно независимых векторов.

Схема метода Розенброка:

1. Задаем начальную точку , полагаем,, и орты исходной системы координат обозначаем.

2. Исходя из точки по формулам (7), (8) выполняем одну итерацию пометоду Гаусса-Зейделя – получаем точку и совокупность векторов,,...,.

3. Если одно из стандартных условий окончания итераций

   (9)

4. выполнено, то полагаем, и заканчиваем вычисления. Иначе переходим к п.4).

5. На основе векторов находим векторы:

   (10)

7. С помощью процедуры ортогонализации Грамма-Шмидта (3) –(6) выполняем переход от системы векторов к системе векторов, полагаем=+1 и переходим к п. 2

Заметим, что из формулы (10) следует равенство .

По сравнению с методом Гаусса-Зейделя и методом Хука-Дживса метод Розенброка имеет, как правило, более высокую эффективность на овражных функциях с не прямолинейным оврагом.

Метод Розенброка иллюстрирует рис. 1, на котором показаны линии уровня функции Химмельблау (=2),

Рис. 1.  Траектория поиска минимума функции Химмельблау методом Розенброка.

Метод сопряженных направлений

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в-мерном евклидовом пространстве,

(1)

Введем прежде следующие понятия: векторы , принадлежащие пространству, называютсявекторами сопряженными относительно матрицы A (A – ортогональными векторами), если для всех.

В методе сопряженных направлений применяется итерационная формула метода Гаусса-Зейделя в виде, близком к использованному в параграфе 6.3.

Положим и пусть,,...,- орты используемой системы координат. Тогда итерационную формулуметода Гаусса-Зейделя можно записать в виде

(2)

где коэффициенты находятся из условий

(3)

Схема метода сопряженных направлений:

1. Задаем начальную точку и полагаем=0,=1.

2. Последовательно для =1,2,...,по формулам (2), (3) находим точки,,.

3. Исходя из точки , еще раз находим минимум функции() вдоль первого координатного направления - вычисляем координаты точки

   (4)

4. где коэффициент находится из условия

   (5)

6. Исходя из точки , находим минимум функциивдоль вектора- вычисляем

   (6)

7. где коэффициент находится из условия

   (7)

9. Если одно из стандартных условий окончания итераций

   (8)

10. выполнено, то полагаем, и заканчиваем вычисления. Иначе - полагаем=+1 и переходим к п.2)

Метод сопряженных направлений иллюстрирует рис. 1, на котором показаны линии уровня функции Химмельблау (=2).

Рис. 1.  Траектория поиска минимума функции Химмельблау методом сопряженных направлений.

Рассмотрим еще один пример – см. рис. 2, на котором показаны линии уровня двумерной квадратичной функции

(9)

Линии уровня получены с помощью MATLAB-программы, приведенной в параграфе 6.1.

Рис. 2.  Траектория поиска минимума квадратичной функции (9) методом сопряженных направлений.

Произвольную -мерную квадратичную функцию можно записать в виде

(10)

где – квадратная*матрица,–*1 столбец,– скалярная константа. Например, если положить

то имеем функцию (9):

Утверждение 1. В случае минимизации двумерной квадратичной функции (10) методом сопряженных направлений, направления ,являются-ортогональными.

Доказательство (см. рис. 2). По определению -ортогональности для доказательства утверждения достаточно показать, что скалярное произведение

(11)

Легко видеть, что производная функции (10) равна . ПоэтомуПодставляя этот результат в выражение (11), получим.

Последнее равенство следует из ортогональности пар векторов

Утверждение 1 объясняет название рассмотренного метода.

Заметим, что при минимизации квадратичной функции методом сопряженных направлений минимум достигается за одну итерацию.

Симплекс-метод

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в-мерном евклидовом пространстве,

(1)

Регулярный симплекс и некоторые операции над ним.

Регулярным симплексом в пространстве называется правильный многогранник, образованный-ой равноотстоящими друг от друга вершинами. Для случая– это равносторонний треугольник, для случая– тетраэдр.

Если в пространстве необходимо построитьрегулярный симплекс, одна из вершин которого находится в точке , то координаты вершин такого симплекса удобно задавать с помощьюматрицы

(2)

Здесь -й столбец представляет собой координаты-й вершины симплекса,;

(3)

-длина ребра симплекса.

Например, регулярный симплекс в двумерном пространстве с одной из вершин в начале координат (когдаопределяетсяматрицей

и имеет вид, представленный на рис. 1.

Рис. 1.  Регулярный симплекс в пространстве R² с одной из вершин в начале координат.

В алгоритме симплекс-метода используется следующее важное свойство регулярного симплекса: если одну из вершин регулярного симплекса перенести на надлежащее расстояние вдоль прямой, соединяющей данную вершину и центр тяжести оставшихся вершин, то вновь получится регулярный симплекс (см. рис. 2).

Будем называть эту процедуру отражением вершины симплекса относительно центра тяжести остальных вершин.

Рис. 2.  Отражение вершины X₁ регулярного симплекса в пространстве R² относительно центра тяжести X_c остальных вершин.

Пусть - векторы координат вершинрегулярного симплекса. Тогда при выполнении операции отражения -й вершины симплекса имеет место следующая связь координат этой вершины и новой вершины:

(4)

Здесь

(5)

вектор координат центра тяжести остальных вершин симплекса (за исключением отраженной вершины )

Таким образом, после отражения -й вершины симплекса с координатами вершин, получаем новый симплекс с координатами вершин

(6)

Кроме операции отражения вершины симплекса симплекс-метод может использовать операцию редукции симплекса (см. рис. 3) - уменьшение длин всех ребер симплекса на одну и ту же величину.

Рис. 3.  Редукция вершин регулярного симплекса в пространстве R² к вершине X₁.

Пусть - векторы координат вершинрегулярного симплекса. Тогда при выполнении операции редукции вершин этого симплекса к вершине новые координаты остальных вершин симплекса определяются по формуле

=+(-),[1,+1],,

где - коэффициент редукции. Рекомендуется использовать.

Таким образом, после редукции вершин симплекса к вершинеполучаем новый симплекс с координатами вершин

(7)

Схема простейшего варианта симплекс-метода.

Суть симплекс-метода раскрывает его простейший вариант.

1. Задаем начальную точку , длину ребра симплексаи полагаем=0.

2. По формулам (2), (3) находим координаты всех вершин симплекса.

3. Вычисляем значения минимизируемой функции во всех вершинах симплекса.

4. Находим максимальное из значений функции в вершинах симплекса

5. По формулам (5), (6) отражаем вершину относительно центра тяжести остальных вершин симплекса – получаем новый симплекс с координатами вершин.

6. Вычисляем значениеминимизируемой функции в новой вершине симплекса.

7. Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции () принимаем ту вершину симплекса, в которой() имеет минимальное значение, и заканчиваем вычисления. Иначе полагаем=+1 и переходим к п. 4

Поскольку размер симплекса в простейшем варианте симплекс-методе фиксирован, в качестве условия окончания итераций в данном случае можно использовать условие

(8)

где - требуемая точность решения по,- номер произвольной вершины симплекса. Отметим, что выражение в левой части неравенства (8) есть максимальная разность значений функции() в двух вершинах симплекса.

Простейший вариант симплекс-метода иллюстрирует рис. 4, на котором показаны линии уровня функции Химмельблау (=2).

Рис. 4.  Траектория поиска минимума функции Химмельблау простейшим симплекс-методом.

Модифицированный симплекс-метод.

Рассмотренный простейший симплекс-метод склонен к зацикливанию и медленно сходится, если длина ребра симплекса выбрана малой (выбор же большой длины ребра симплекса обеспечивает высокую скорость сходимости, но дает малую точность решения). Поэтому в вычислительной практике используются различные модификации простейшего метода, направленные на преодоление его указанных недостатков.

Основной идей модифицированного симплекс-метода является изменение по некоторому правилу размера симплекса в процессе поиска. При этом наряду с условием (8) в качестве условия окончания итераций можно использовать условие

(9)

где - текущая длина ребра симплекса,- требуемая точность решения по.

Обычно размер симплекса изменяется при выполнении следующих условий:

• при «накрытии» симплексом дна оврага или точки минимума;

• при циклическом движении.

«Накрытие» симплексом дна оврага или точки минимума. Пусть - вершина, которая получилась на-ой итерации в результате отражения вершины. Так что координаты вершин нового симплекса равны.

Ситуация интерпретируется как «накрытие» этим симплексом дна оврага или точки минимума и простейшийсимплекс-метод модифицируется следующим образом (см. рис. 5):

1. Полагаем =+1 (если=+2, то полагаем=1);

2. Выполняем отражение -ой вершины симплекса;

3. Если ()>() и не все вершины перебраны, то переходим к п.1.

4. Иначе - продолжаем итерации по схеме простейшего симплекс-метода

Рис. 5.  Траектория поиска минимума функции Розенброка модифицированным симплекс-методом при «накрытии» дна оврага. Пунктиром показаны отвергнутые симплексы.

Циклическое движение. Ситуация, когда некоторая вершина симплекса не исключается на протяжении итераций, интерпретируется как «зацикливание» алгоритма. Простейшийсимплекс-метод модифицируется в этом случае следующим образом:

1. Находим вершину текущего симплекса , в которой функция() принимает наименьшее значение

2. По формуле (7) выполняем редукцию симплекса к вершине.

3. Продолжаем итерации по схеме простейшего симплекс-метода

Здесь количество итераций рекомендуется находить из условиягде*- символ ближайшего целого большего.

Метод деформируемого многогранника (Нелдера-Мида)

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в-мерном евклидовом пространстве,

(1)

В случае если функция () являетсяовражной функцией, эффективность симплекс-метода при решении задачи (1) значительно снижается в силу того, что регулярный симплекс нельзя «вытянуть» вдоль оврага. Метод Нелдера-Мида (метод деформируемого многогранника) является развитием симплекс-метода и использует в процессе поиска деформацию (изменение размеров и формы) текущего симплекса (не обязательно регулярного).

Метод использует следующие операции над симплексами:

• отражение;

• редукция;

• сжатие;

• растяжение.

Отражение вершины симплекса относительно центра тяжести остальных вершин (см. параграф 5, рис. 1). В результате отражения -й вершины симплекса с координатами вершин, получаем новый симплекс с координатами вершин

(2)

где

(3)

вектор координат центра тяжести остальных вершин симплекса (за исключением отраженной вершины ).

Рис. 1.  Отражение вершины X₁ симплекса в пространстве R² относительно центра тяжести X_c остальных вершин.

Редукции симплекса (см. параграф 5, рис. 2) - уменьшение длин всех ребер симплекса в одно и то же количество раз. В результате выполнения редукции вершин симплекса к вершинеполучаем новый симплекс с координатами вершин

(4)

где - коэффициент редукции.

Рис. 2.  Редукция вершин симплекса в пространстве R² к вершине X₁.

Сжатие симплекса (см. рис. 3). В результате выполнения сжатия симплекса ,[1,+1] в направленииполучаем новый симплекс с координатами вершин

(5)

где - коэффициент сжатия,- вектор координат центра тяжести остальных вершин симплекса (см. (3)).

Рис. 3.  Сжатие симплекса в пространстве R² в направлении (X₁-X_c).

Растяжение симплекса (см. рис. 4). В результате выполнения растяжения симплекса в направленииполучаем новый симплекс с координатами вершин

(6)

где - коэффициент растяжения,- вектор координат центра тяжести остальных вершин симплекса (см. (3)).

Рис. 4.  Растяжение симплекса в пространстве R² в направлении (X₁-X_c).

Схема метода Нелдера-Мида.

Симплекс с вершинами обозначим.

1. Задаем начальную точку , длину ребра симплексаи полагаем=0.

2. Находим координаты ,[1,+1] всех вершинрегулярного симплекса с длиной ребра. Вычисляем значения() минимизируемой функции во всех вершинах симплекса.

3. Среди вершин симплекса находим вершиныв которых функция() принимает, соответственно, наименьшее, наибольшее и следующее за максимальным значения, а также находим значения функции() в этих точках:

4. По формулам (2), (3) выполняем отражение вершину симплекса относительно центра тяжести остальных вершин симплекса – получаем новый симплекс. Вычисляем значение() минимизируемой функции в новой вершине симплекса.

5. Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции () принимаем ту вершину симплекса, в которой() имеет минимальное значение, и заканчиваем вычисления.

6. Если и, то переходим к п.7 (растяжению симплекса) - см. рис. 5. Если , но, то переходим к п.3 (отражению) – см. рис. 6. Если, то переходим к п.8 (сжатию симплекса) – см. рис. 7, рис. 8.

7. Ситуация и. По формуле (6) выполняемрастяжение симплекса в направлении- получаем новый симплекс. Вычисляем значение минимизируемой функции в новой вершине симплекса. Если, то полагаеми переходим к п.3 (отражению вершины симплекса). Иначе полагаем и переходим к п.3 (отражению вершины симплекса) с симплексом (т.е. не используем результаты растяжения).

8. Ситуация . По формуле (5) выполняемсжатие симплекса в направлении- получаем новый симплекс. Вычисляем значение минимизируемой функции в новой вершине симплекса. Если, то полагаем=+2 и переходим к п.3 (отражению вершины симплекса). Иначе по формуле (4) выполняем редукцию симплекса к вершине- получаем новый симплекс. Вычисляем значение минимизируемой функции во всех новых вершинах симплекса. Полагаем=+1 и переходим к п.3 (отражению симплекса)

Рис. 5.  Ситуация, когда метод Нелдера-Мида использует успешное растяжение симплекса.

Рис. 6.  Ситуация, когда метод Нелдера-Мида использует успешное отражение симплекс.

Рис. 7.  Ситуация, когда метод Нелдера-Мида использует успешное сжатие симплекс.

Рис. 8.  Ситуация, когда метод Нелдера-Мида использует редукцию после неудачного сжатия симплекса. Пунктиром показаны отвергнутые (неудачные) итерации.

На рис. 5 - рис. 8 минимизируемой функцией () являетсяфункция Химмельблау.

В качестве условия окончания итераций в методе Нелдера-Мида можно использовать условие

где - требуемая точность решения по,[1,+1] - номер произвольной вершины симплекса. Можно также завершать итерации, когда длина максимального из ребер текущего симплекс станет меньше или равна- требуемой точности решения по.

Изложенная схема метода Нелдера–Мида имеет тот недостаток, что для сильно овражных функций может происходить вырождение («сплющивание») симплекса. Поэтому к рассмотренной схеме метода Нелдера-Мида добавляется этап периодического (через итераций)восстановления симплекса, который заключается в следующем:

• в текущем симплексе выбираются две «лучшие» вершины и определяется расстояние между ними ;

• исходя из «лучшей» вершины текущего симплекса строится новый симплекс, длина ребра которого принимается равной (см. параграф 5).