2. Принцип “дальнего соседа”.
Решение задачи:
Расчеты расстояний
аналогичны
предыдущему принципу.
1. Формулу: =КОРЕНЬ((B3-B3)^2+(B4-B4)^2) помещаем в ячейку В9 и рассчитываем расстояние р11, затем в ячейке В10 - расстояние р12 по формуле: =КОРЕНЬ((B3-C3)^2+(B4-C4)^2) и т.д., пока не будет произведен расчет расстояний между всеми шестью объектами (ячейки В9:В24):
p11=0; p12=2.83; p13=3.16; p14=10.20; p15=12.17;
p16=13.6; p23=3.16; p24=8.94; p25=10.77; p26=12.53;
p34=7.07; p35=9.06; p36=10.44; p45=2; p46=3.61; p56=2.24.
Полученные данные помещаем в таблицу (матрицу) -ячейки E11:K17 (табл.12). Из матрицы расстояний следует, что объекты 4 и 5 имеют наименьшее значение P45=2.00 и поэтому объединяются в один кластер. Для расчета расстояния используется формула: =МИН(G12:K12;H13:K13;I14:K14;J15:K15;K16) в ячейке F19.
После объединения имеем пять кластеров.
|
Номер кластера |
1 |
2 |
3 |
4 |
5 |
|
Состав кластера |
(1) |
(2) |
(3) |
(4,5) |
(6) |
Для решения задачи воспользуемся принципом “дальнего соседа”: искомое расстояние между кластерами S(4), S(5) p15=12.17, т. к. p15=12.17 больше p14=10.20, поэтому матрица расстояний примет вид (ячейки E22:J27):
|
|
|
⌐─────¬ |
|
|
|
| |
|
|
№ п/п |
1 |
2 |
3 |
4,5 |
6 |
|
|
┌ |
1 |
0 |
2.83 |
3.16 |
12.17 |
13.60 |
|
|
└ |
2 |
|
0 |
3.16 |
10.77 |
12.53 |
|
|
|
3 |
|
|
0 |
9.06 |
10.44 |
|
|
|
4,5 |
|
|
|
0 |
3.61 |
|
|
|
6 |
|
|
|
|
0 |
|
Для расчета расстояния применим формулу =МИН(G23;H23:H24;I23:I25;J23:J26), помещенную в ячейке F29, получив расстояние PMIN=P2,3=2.83. Объединяем кластеры 1и 2 в один.
Таблица 12
Исходные данные
После объединения имеем матрицу расстояний, отображенную в табл.13 и следующие кластеры: S(1,2), S(3), S(4,5), S(6).
3. Вновь находим матрицу расстояний, помещаем рассчитанные значения в ячейки E32 - I36 и объединяем объекты 1,2 и 3, имеющие расстояние PMIN=P1,2=3.16 (формула =МИН(G33:I33;H34:I34;I35) в ячейке F38). Расстояние между остальными кластерами остается без изменения. В результате имеем три кластера: S(1,2,3), S(4,5), S(6).
Объединим теперь объекты 4,5 и 6, расстояние между которыми равно: PMIN=P1,2,3=3.61 (формула =МИН(G42:H42;H43) в ячейке F46). Матрица расстояний размещается в ячейках E41-H44.
Таким образом, при проведении кластерного анализа по принципу “дальнего соседа” получили два кластера: S(1,2,3), S(4,5,6), расстояние между которыми равно:
P(1,2,3); (4,5,6) = 13,60.
Таблица 13
Расчетные значения
Результаты иерархической классификации объектов представлены на рис. 14 в виде дендрограммы.
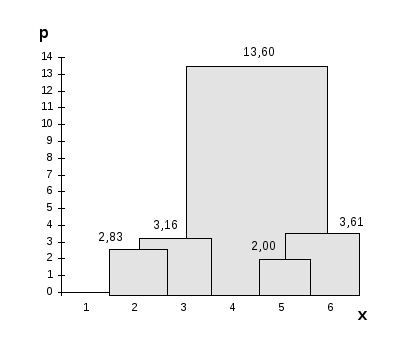
Рис. 14. Дендрограмма
3.3.3. Варианты заданий
Провести разбиение объектов на основании данных, приведенных в таблице. Выбор метода решения провести самостоятельно, построить график зависимости данных.
Вариант 1.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
2 |
4 |
15 |
12 |
14 |
15 |
|
х2 |
8 |
8 |
5 |
6 |
6 |
4 |
где х1 - объем выпускаемой продукции;
х2 - среднегодовая стоимость основных промышленно-производственных фондов.
Вариант 2.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
5 |
6 |
5 |
10 |
11 |
10 |
|
х2 |
10 |
12 |
13 |
9 |
9 |
7 |
где х1 - рентабельность, %
х2 - производительность труда, тыс.руб\чел.
Вариант 3.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
23.4 |
17.5 |
9.7 |
18.2 |
6.6 |
8 |
|
х2 |
9.2 |
5.2 |
5.5 |
9.4 |
7.6 |
5.7 |
где х1 - объем реализованной продукции;
х2 - затраты на рекламу
Вариант 4.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
2.49 |
1.5 |
1.15 |
1.62 |
2.74 |
3.15 |
|
х2 |
0.38 |
0.51 |
0.28 |
0.29 |
0.34 |
0.4 |
где х1 - объем выпускаемой продукции;
х2 - объем заемных средств
Вариант 5.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
34.8 |
31.2 |
32.1 |
35.7 |
30.3 |
34.2 |
|
х2 |
128 |
112 |
123 |
128 |
116 |
124 |
где х1 - объем продаж
х2 - капиталовложения
Вариант 6.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
8.22 |
4.33 |
6.45 |
6.39 |
4.92 |
6.5 |
|
х2 |
0.25 |
0.49 |
0.51 |
0.27 |
0.32 |
0.43 |
где х1 - урожайность зерновых
х2 - доля внесения удобрений
Вариант 7.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
8.22 |
4.33 |
6.45 |
6.39 |
4.92 |
6.5 |
|
х2 |
0..42 |
0.39 |
0.51 |
0.42 |
0.53 |
0.49 |
где х1 - объем выпускаемой продукции;
х2 - затраты на электроэнергию
Вариант 8.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
9.42 |
6.33 |
7.45 |
10.0 |
6.6 |
9.1 |
|
х2 |
0.15 |
0.48 |
0.62 |
0.32 |
0.5 |
0.9 |
где х1 - число автостоянок на 1000 автомашин
х2 - число сервисных предприятий по ремонту
Вариант 9.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
9.42 |
6.33 |
7.45 |
10.0 |
6.6 |
9.1 |
|
х2 |
1.9 |
0.88 |
1.09 |
2.62 |
1.35 |
1.89 |
где х1 - объем выпускаемой продукции;
х2 - производительность труда
Вариант 10.
Исходные данные
|
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
9.42 |
6.33 |
7.45 |
10.0 |
6.6 |
9.1 |
|
х2 |
1.9 |
0.88 |
1.09 |
2.62 |
1.35 |
1.89 |
где х1 - объем выпускаемой продукции;
х2 - доля высокотехнологичного обрудования в производстве