методичка по гидравлика № 130

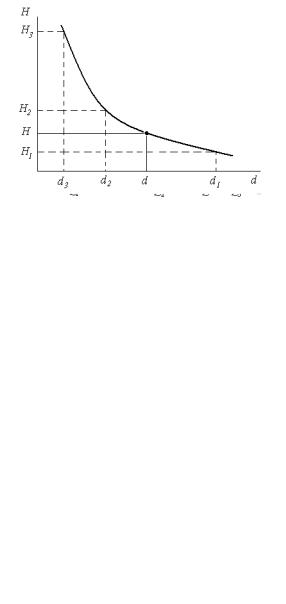
Рисунок 8.3

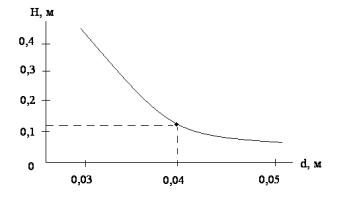
Для третьої задачі рівняння (8.6) найбільш зручно розв’язувати відносно діаметра d графічним способом. Задають приблизні значення d1, d2 , d3 , обчислюють за формулою (8.6) відповідні значення H1, H2 , H3 ;

будують графік залежності H f d (рисунок 8.4), із якого знаходять

діаметр, який відповідає заданому напору. За найденим розрахунковим значенням діаметра вибирають найближчий до нього стандартний діаметр труби.

Рисунок 8.4

8.3 Простий трубопровід змінного діаметра

Розглянемо напірно самопливний рух рідини в простому трубопроводі, який складається із двох послідовно з’єднаних труб різних діаметрів d1 і d2

та довжини l1 і l2 . При цьому обмежимося випадком, коли рідина витікає з трубопроводу в атмосферу (рисунок 8.5), і будемо вважати, що діаметр

d2 d1 .

Із рівняння нерозривності, записаного для перерізів 0-0 на поверхні рідини в резервуарі і 2-2 в кінці другої ділянки трубопроводу, одержуємо:

V0 2

V2 0

або, враховуючи, що 2 0 ,

V0 V2 .

61

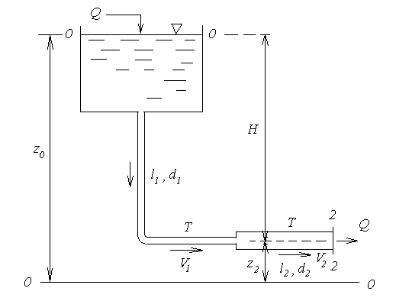
Рисунок 8.5

При послідовному з’єднанні труб втрати напору від перерізу 0-0 до перерізу 2-2 потрібно додавати, тому рівняння Бернуллі для цих перерізів можемо записати у вигляді

ділянках відповідно; останній додаток у правій частині рівняння (8.9) виражає додатковий опір у місці з’єднання труб, зумовлений різким розширенням потоку.

Отже, одержано розрахункове рівняння (8.11) для простого трубопроводу, який складається з двох послідовно з’єднаних труб різних діаметрів. Гідравлічний розрахунок такого трубопроводу зводиться до розв’язання трьох основних задач, аналогічних задачами гідравлічного розрахунку

62

простого трубопроводу сталого діаметра. Рівняння (8.11) дозволяє розв’язати першу і другу із цих задач. Третя задача, що пов’язана з визначенням діаметрів труб d1 і d2 , стає невизначеною, оскільки маємо одне рівняння з

двома невідомими. Для можливого розв’язання цієї задачі потрібно задати ще одне рівняння, яке пов’язує діаметри d1 і d2 , наприклад, співвідношення

d2 m . d1

Розрахункові рівняння (8.6) в (8.11), одержані для напірно самопливного руху рідини, коли напір H є геометричним і утворений за рахунок різниці відміток початкового і кінцевого живих перерізів відносно довільної площини порівняння, тобто H z1 z2 . Однак у випадку руху рідини

у простому трубопроводі під дією напору H , який розвиває насос, розрахункові рівняння (8.6) і (8.11) набувають вигляду

де 1 2 – коефіцієнт місцевого опору, зумовленого раптовим розширенням чи звуженням потоку у місці стику труб; – коефіцієнт пов’язаний з різницею

швидкісних напорів у початковій і кінцевій ділянках трубопроводу. При переході вузької труби у широку коефіцієнт

1 m2 0,

апри переході широкої труби у вузьку –

1 n2 0,

де m – ступінь розширення, а n - ступінь звуження потоку у місці з’єднання труб.

Три основні задачі для рівнянь (8.12) і (8.13) формуються і розв’язуються аналогічно, як і три основні задачі для рівнянь (8.6) і (8.11).

Наведемо приклади розв’язування вищезазначених основних задач гідравліки на випадок напірно самопливного руху води у довгому

в’язкості води v 1 10 6 м2/с.

Розв’язування. Насамперед визначимо число Re за формулою (8.7):

Так як Re 31847 4000 , то режим руху турбулентний.

Оскільки труба гідравлічно гладка, коефіцієнт гідравлічного тертя визначимо за формулою Блазіуса (6.6):

63

0,3164Re0,25 318470,31640,25 0,0237 .

Для визначення напору H використовуємо залежність (8.6), нехтуючи в ній доданком , оскільки за умовою задачі трубопровід довгий:

Задача 2. Визначити витрату Q , якщо H 0,128 м, d 0, 04 м, l 5 м. Розв’язування. Для визначення витрати Q розв’яжемо рівняння (8.8)

методом послідовних наближень з точністю до 1%.

Упершому наближенні приймаємо 0,03 . Тоді одержуємо, згідно

з(8.8),

Визначаємо число Re за формулою (8.7):

Відношення

Q 0,000992 1,086 . Q 0,000913

Отже, розбіжність між другим та першим наближеннями витрати складає 8,6%. Оскільки така точність наближення нас не задовольняє, аналогічно знаходимо третє наближення Q .

наближення складає 0,8% і є цілком задовільною. Так що шукана витрата

Q 0,001м3/с.

64

Задача 3. Визначити діаметр труби d для заданих H 0,128 м,

Q 0,001м3/с, l 5 м.

Розв’язування. Використовуємо рівняння (8.6) і розв’яжемо його

заданому напору H 0,128 м відповідає розрахунковий діаметр d 0, 04 м.

Рисунок 8.6

Контрольні питання

1.Який трубопровід називається простим?

2.Що таке довгий і короткий трубопроводи?

3.Як одержують розрахункове рівняння для простого трубопроводу сталого діаметра?

4.Три основні задачі гідравлічного розрахунку простого трубопроводу?

5.В чому полягає особливість третьої задачі гідравлічного розрахунку простого трубопроводу змінного діаметра?

65

ЛЕКЦІЯ 9

Гідравлічний розрахунок складних трубопроводів

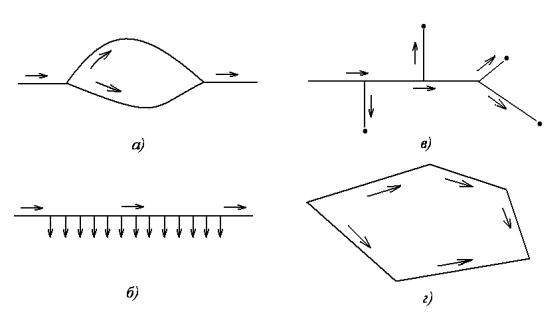
Із різноманітних можливих схем складних трубопроводів основними є: паралельне з’єднання, трубопроводи із змінною витратою по путі, розгалужений і однокільцевий трубопроводи (рисунок 9.1, а, б, в, г). Ці схеми можна розглядати як елементи більш складних схем трубопроводів.

Розглянемо методи гідравлічного розрахунку трубопроводів на випадки паралельного з’єднання та змінної витрати по путі.

Рисунок 9.1

9.1 Паралельне з’єднання

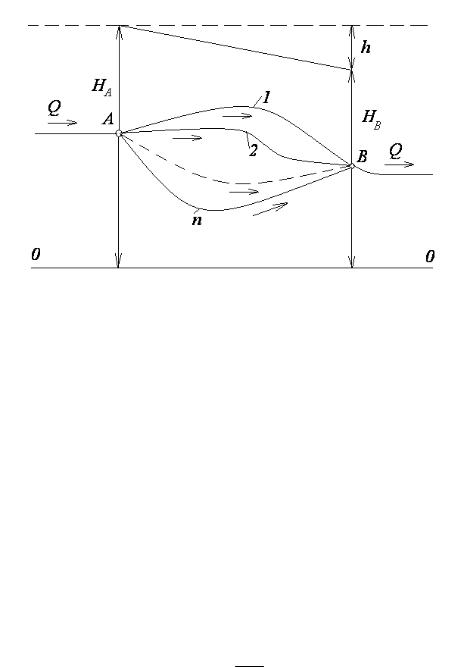
Нехай трубопровід в певній точці А розгалужується на n труб, які потім знову з’єднуються у точці В і переходять в одну трубу. Витрата рідини Q в

основному трубопроводі до розгалуження і після з’єднання труб одна і та сама (рисунок 9.2). Такого роду трубопроводи, маючи спільні вузли у початковому і кінцевому перерізах, забезпечують підвищену надійність їх роботи, позаяк у випадку виходу із ладу одного із них рідина буде поступати по других.

Слід зазначити, що оскільки у вузлі розгалуження трубопроводу А тиск

буде однаковим для усіх труб, що розгалужуються. Також для усіх труб буде

66

втрати напору у всіх трубах, з’єднаних паралельно, однакові і дорівнюють h H A HB . Так що при паралельній роботі труб принцип складання втрат

напору в окремих трубах, властивий для послідовно з’єднаних труб різних діаметрів і довжин, стає неприйнятним.

Рисунок 9.2

При гідравлічному розрахунку трубопроводу з паралельним з’єднанням основна задача полягає у визначенні витрат Q1, Q2 , ... Qn в паралельних гілках

труб та у визначенні втрати напору між вузлами А і В, якщо відомі загальна витрата Q , діаметри і довжини паралельних гілок труб.

Вважається, що відносна шорсткість цих труб теж відома. Для розв’язання цієї задачі потрібно скласти систему алгебраїчних рівнянь, які пов’язують розміри труб, витрати рідини і втрати напору на кожній із паралельних гілок труб.

Запишемо вираз для втраченого напору h на будь-якій і-вій гілці паралельних труб:

який, ураховуючи, що

Vi 4Qi ,

di2

можна переписати так:

Введемо позначення

67

і перепишемо вираз (9.1) у спрощеному вигляді

Оскільки величина втраченого напору hi на кожній із паралельних гілок труб однакова і дорівнює h , то можемо написати, на підставі виразу (9.3),

тому повинна бути доповнена ще одним рівнянням. Таким рівнянням є рівняння балансу витрат:

Аналітичний розв’язок системи алгебраїчних рівнянь (9.5) і (9.6) можна одержати лише за умови, що усі коефіцієнти гідравлічного тертя і коефіцієнт місцевих опорів , які входять до (9.2), не залежать від числа Re .

У такому разі величини B1, B2 ,...Bn постійні і не залежать від Q1,Q2 ,...Qn

відповідно.

За таких умов система рівнянь (9.5) і (9.6) розв’язується наступним чином. В системі (9.5) послідовно виключаємо h з першого і другого рівнянь, потім з першого і третього ... та з першого і n -го:

B2Q22 B1Q12 ;

B3Q32 B1Q12 ; .

. . . . . . . . . . . . . .

BnQn2 B1Q12 .

Звідси знаходимо

68

Підставивши ці вирази для Qi у рівняння (9.6), будемо мати:

Звідси одержуємо вираз для витрати першої гілки Q1 :

Знаючи величину Q1 , визначаємо послідовно Q2 ,Q3 ,...Qn за відповідними

формулами (9.7). Втрачений напір знаходимо із будь-якого рівняння системи (9.5); наприклад,

Отже, одержано аналітичний розв’язок задачі за передумови, що усі коефіцієнти і , а також коефіцієнти В не залежать від числа Рейнольдса

Re . Тому знайдені розрахункові значення Q1,Q2 ,...Qn та h можуть бути

наближеними.

Аби одержати більш точні значення витрат у всіх гілках труб і втрати напору визначають число Re для кожної гілки окремо:

коефіцієнтів B1, B2 ,...Bn . Підставляючи уточнені значення B1, B2 ,...Bn у (9.8), знаходять уточнену витрату

69

. . . . . . . . . . . . . .

для усіх гілок труб.

Уточнене значення втрати напору h можна одержати, зокрема, за формулою:

h B1Q1 2 .

При необхідності роблять подальші уточнення повторним аналогічним розрахунком.

9.2 Змінна витрата по путі

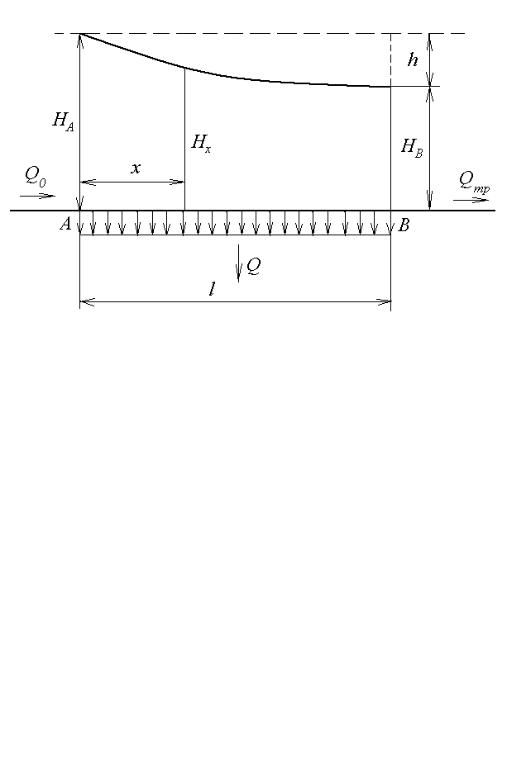
Розглянемо горизонтальний трубопровід, на ділянці АВ якого здійснюється неперервний відбір рідини з питомою (на одиниці довжини) витратою q (рисунок 9.3). Зрозуміло, що витрата уздовж цієї ділянки

неперервно зменшується, тому рух рідини відбувається із змінною витратою,

тобто Q V const .

Рисунок 9.3

Позначимо через Q0 , Q і Qтр – витрати трубопроводу перед ділянкою

АВ, на самій ділянці і за нею відповідно. Витрату Q називають зазвичай скидною витратою, а Qтр – транзитною витратою.

Задача гідравлічного розрахунку трубопроводу із змінною витратою по путі полягає у визначенні скидної і транзитної витрат Q і Qтр , а також втрати

70