
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •7. Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення дискретної випадкової величини, такої що задана законом розподілу:
- •8. Відомі математичні сподівання а та середньоквадратичне відхилення нормально розподіленої випадкової величини х. Знайти ймовірність попадання заданої величини в даний інтервал (, )
- •9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини х потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •1. Знайти ймовірність того, що при підкиданні 2-х гральних кісток на них випадає однакова кількість очок.
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •1. Знайти ймовірність того, що при підкиданні 2-х гральних кісток на них випадає однакова кількість очок.
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
- •10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
Міністерство освіти та науки, Молоді та спорту України
ДЕРЖАВНИЙ ЕКОНОМІКО-ТЕХНОЛОГІЧНИЙ
УНІВЕРСИТЕТ ТРАНСПОРТУ
Кафедра вищої математики
Розрахункова робота
з дисципліни "Теорія ймовірностей і математична статистика"
для студентів денної форми навчання
2-МО
Київ-2012
Варіант 1
1. Знайти ймовірність того, що при підкиданні 2-х гральних кісток на них випадає однакова кількість очок.
2. Проводиться профілактичний огляд 8 вагонів, серед яких 2 плацкартних та 6 купейних. Яка ймовірність того, що перші два вагони, які оглядаються будуть купейними? (Вагони при огляді вибирають випадковим чином)
3. Кількість колій для посадки – 12. Відомо, що в середньому 40% часу на колії знаходяться потяги. Яка ймовірність того, що у випадковий момент часу на трьох коліях знаходяться потяги?
4. Серед пасажирів потягу № 7 20% складають пасажири з Праги, 10% - з Братислави та 70% - із Львова. Серед пасажирів з Праги 20% громадян України, серед пасажирів з Братислави 10% громадян України, а серед пасажирів із Львова 80% громадян України. Яка ймовірність того, що навмання обраний пасажир є громадянином України?
5. Підручник виданий тиражем в 10000 екземплярів. Ймовірність того, що підручник відредаговано неправильно, дорівнює 0,0001. Знайти ймовірність того, що в тиражі знаходяться 3 браковані книги.
6. Неперервна випадкова величина Х задана своєю щільністю розподілу ймовірностей f(x). Знайти коефіцієнт а, функцію розподілу F(x), побудувати графіки f(x), F(x). Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення цієї величини. Знайти ймовірность того, що Х прийме занчення з інтервалу (; ).
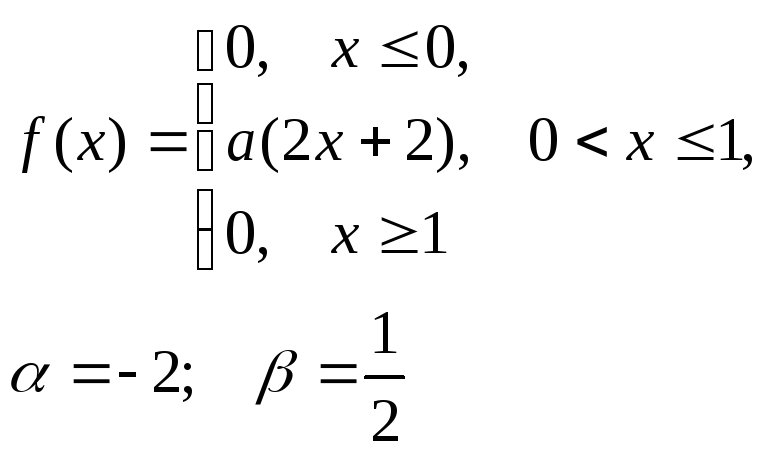
7. Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення дискретної випадкової величини, такої що задана законом розподілу:
|
Хі |
-6,1 |
-5,3 |
-4,8 |
-3,5 |
-2,4 |
|
Рі |
0,10 |
0,14 |
0,19 |
|
0,20 |
8. Відомі математичні сподівання а та середньоквадратичне відхилення нормально розподіленої випадкової величини Х. Знайти ймовірність попадання заданої величини в даний інтервал (, )
![]()
9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини Х потрібно:
а) побудувати інтервальний статистичний розподіл вибірки;
б) побудувати гістограму частот та емпіричну функцію розподілу;
в) знайти точкові оцінки математичного сподівання та дисперсії випадкової величини Х;
|
13 |
14 |
23 |
33 |
25 |
12 |
13 |
29 |
22 |
10 |
|
11 |
12 |
21 |
23 |
29 |
23 |
25 |
27 |
20 |
25 |
|
18 |
19 |
26 |
14 |
25 |
17 |
28 |
26 |
21 |
25 |
|
7 |
35 |
26 |
22 |
16 |
32 |
17 |
24 |
24 |
19 |
|
24 |
18 |
20 |
21 |
28 |
26 |
18 |
21 |
32 |
26 |
10.
За заданим двовимірним статистичним
розподілом вибірки (X,Y) з генеральної
сукупності з ознаками
![]() потрібно:
потрібно:
а)
знайти рівняння вибіркових прямих ліній
регресії
![]() на
на
![]() та
та
![]() на
на
![]() ;
;
б) побудувати графіки одержаних функцій регресії;
в) побудувати довірчий інтервал для вибіркового коефіцієнту кореляції та перевірити гіпотезу про його вагомість;
|
X\Y |
2 |
10 |
18 |
26 |
34 |
42 |
nx |
|
10 |
3 |
2 |
1 |
- |
- |
- |
6 |
|
20 |
1 |
3 |
7 |
3 |
- |
- |
14 |
|
30 |
- |
1 |
10 |
25 |
7 |
- |
43 |
|
40 |
- |
- |
8 |
10 |
6 |
1 |
25 |
|
50 |
- |
- |
- |
2 |
6 |
4 |
12 |
|
ny |
4 |
6 |
26 |
40 |
19 |
5 |
n=100 |
Варіант 2
-
Знайти ймовiрнiсть того, що при киданні 3-х гральних кісток в сумі випаде 4 очка.
-
Серед 10 пасажирів черги до залізничної каси 4 студенти. Яка ймовірність того, що двоє навмання обраних пасажири – студенти?
-
На митницю прибувають потяги з однотипною продукцією трьох виробників А,В та С. Виробник А постачає 70% продукції, В – 20%, С – 10%. Серед продукції виробника А – 5% продукції, що не відповідає стандартам якості, В – 2%, С – 1%. Митник навмання бере деяку одиницю продукції, яка ймовірність того, що вона не відповідає стандартам якості.
-
Відомо, що студенти становлять 20% від загальної кількості пасажирів. Знайти ймовірність, що серед чотирьох пасажирів купе 2 студенти?
-
Верстат-автомат виготовляє деталі. Ймовірність того, що виготовлена деталь виявиться пошкодженою, дорівнює 0,01. Знайти ймовірність того, що серед 3000 деталей 2 виявляться пошкодженими.
-
Неперервна випадкова величина Х задана своєю щільністю розподілу ймовірностей f(x). Знайти коефіцієнт а, функцію розподілу F(x), побудувати графіки f(x), F(x). Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення цієї величини. Знайти ймовірность того, що Х прийме занчення з інтервалу (; ).

-
Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення дискретної випадкової величини, такої що задана законом розподілу:
|
Хі |
1,2 |
2,3 |
3,7 |
4,2 |
5,1 |
|
Рі |
0,08 |
0,18 |
0,28 |
0,32 |
|
-
Відомі математичні сподівання а та середньоквадратичне відхилення нормально розподіленої випадкової величини Х. Знайти ймовірність попадання заданої величини в даний інтервал (, )
![]()
9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини Х потрібно:
а) побудувати інтервальний статистичний розподіл вибірки;
б) побудувати гістограму частот та емпіричну функцію розподілу;
в) знайти точкові оцінки математичного сподівання та дисперсії випадкової величини Х;
|
26 |
20 |
24 |
22 |
28 |
19 |
24 |
17 |
18 |
32 |
|
37 |
39 |
25 |
16 |
33 |
36 |
28 |
29 |
24 |
13 |
|
31 |
26 |
24 |
14 |
27 |
33 |
9 |
23 |
13 |
16 |
|
15 |
34 |
25 |
10 |
11 |
23 |
28 |
12 |
24 |
6 |
|
13 |
19 |
26 |
32 |
25 |
22 |
17 |
12 |
30 |
28 |
10. За заданим двовимірним статистичним розподілом вибірки (X,y) з генеральної сукупності з ознаками потрібно:
а)
знайти рівняння вибіркових прямих ліній
регресії
![]() на
на
![]() та
та
![]() на
на
![]() ;
;
б) побудувати графіки одержаних функцій регресії;
в) побудувати довірчий інтервал для вибіркового коефіцієнту кореляції та перевірити гіпотезу про його вагомість;
|
X\Y |
18 |
23 |
28 |
33 |
38 |
43 |
nx |
|
3 |
5 |
8 |
7 |
- |
- |
- |
20 |
|
7 |
1 |
8 |
13 |
3 |
- |
- |
25 |
|
11 |
- |
5 |
20 |
22 |
10 |
2 |
59 |
|
15 |
- |
- |
9 |
12 |
8 |
3 |
32 |
|
19 |
- |
- |
- |
2 |
5 |
7 |
14 |
|
ny |
6 |
21 |
49 |
39 |
23 |
12 |
n=150 |
Варіант 3
1. Що ймовірніше: поява при киданні 2 гральний костей в сумі 7 чи 10 балів?
2. Проводиться профілактичний огляд 12 вагонів, серед яких 4 плацкартних та 8 купейних. Яка ймовірність того, що перші два вагони, які оглядаються будуть купейними? (Вагони при огляді вибирають випадковим чином)
3.Кількість колій для посадки – 8. Відомо, що в середньому 60% часу на колії знаходяться потяги. Знайти наймовірніше число колій, на яких знаходяться потяги.
4.Серед пасажирів потягу № 7 10% складають пасажири з Праги, 30% - з Братислави та 50% - із Львова. Серед пасажирів з Праги 20% громадян України, серед пасажирів з Братислави 30% громадян України, а серед пасажирів із Львова 80% громадян України. Яка ймовірність того, що навмання обраний пасажир є громадянином України?
5. Ймовірність влучення в ціль при одному пострілі дорівнює 0,01. Знайти ймовірність того, що при 300 пострілах буде 4 влучення в ціль.
6.Неперервна випадкова величина Х задана своєю щільністю розподілу ймовірностей f(x). Знайти коефіцієнт а, функцію розподілу F(x), побудувати графіки f(x), F(x). Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення цієї величини. Знайти ймовірность того, що Х прийме занчення з інтервалу (; ).
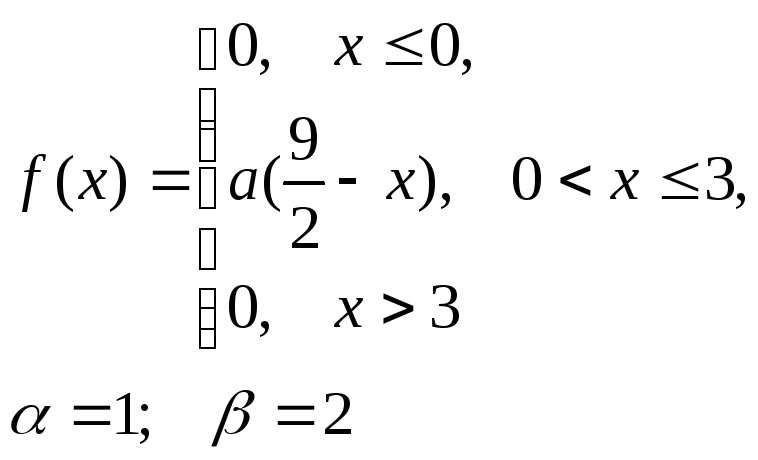
7. Знайти математичне сподівання, дисперсію та середньоквадратичне відхилення дискретної випадкової величини, такої що задана законом розподілу:
|
Хі |
-2,1 |
0,3 |
2,4 |
4,5 |
6,2 |
|
Рі |
0,16 |
0,22 |
0,30 |
|
0,11 |
8. Відомі математичні сподівання а та середньоквадратичне відхилення нормально розподіленої випадкової величини Х. Знайти ймовірність попадання заданої величини в даний інтервал (, )
![]()
9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини Х потрібно:
а) побудувати інтервальний статистичний розподіл вибірки;
б) побудувати гістограму частот та емпіричну функцію розподілу;
в) знайти точкові оцінки математичного сподівання та дисперсії випадкової величини Х;
|
13 |
25 |
17 |
29 |
21 |
33 |
6 |
15 |
20 |
21 |
|
14 |
26 |
18 |
30 |
22 |
34 |
27 |
18 |
10 |
24 |
|
15 |
23 |
31 |
25 |
14 |
19 |
25 |
27 |
15 |
26 |
|
14 |
8 |
23 |
27 |
9 |
11 |
26 |
22 |
30 |
19 |
|
22 |
25 |
13 |
27 |
25 |
19 |
30 |
25 |
26 |
21 |
