6.4 Розгортка конуса

Розгортка конуса складається з бічної поверхні, що є сектором кола, радіус якого дорівнює твірній, а кут визначається за формулою α = 360⁰R/l, та основи конуса.

При побудові розгортки конуса її поверхню найчастіше апроксимують поверхнею піраміди. Для цього основу поділяють на кілька рівних частин (на рисунку 1.49а – на вісім).

Прямий конус має однакові твірні, натуральною величиною яких є твірні, що обмежують фронтальну проекцію конуса (рис. 1.49а).

Нахилений конус має різні твірні. Натуральну величину мають твірні, що обмежують фронтальну проекцію конуса. Натуральну величину всіх інших твірних визначають способом обертання навколо проеціювальної осі (рис. 1.49б).

а) б)

Рисунок 1.49 – Визначення натуральних величин твірних конуса

Бічну поверхню розгортки нахиленого конуса будують способом тріангуляції.

6.5 Розгортка бічної поверхні складної поверхні

Доволі часто у інженерній практиці виникає необхідність будувати розгортки бічних поверхонь, що мають переходи від прямокутного контуру до кола та навпаки. На рисунку 1.50 зліва наведене креслення такого переходу, а справа – наочне зображення його.

Рисунок 1.50 – Зображення складної поверхні

Бічна поверхня пропонованого переходу складається із послідовно розміщених гранних поверхонь та поверхонь конуса. Поверхня симетрична, тому досить виконати половину розгортки бічної поверхні.

Для побудови половини трикутної грані (трикутника 123) необхідно на вільному місці креслення провести вертикальну лінію, на якій відкласти натуральну величину сторони трикутника, наприклад, 12 (фронтальна проекція відрізка 2₂1₂ – натуральна величина). З точки 1 вправо відкласти під прямим кутом до 12 натуральну величину половини основи трикутника (натуральна величина відстані 13 виміряється на горизонтальній площині проекцій). Натуральні величини позначені на кресленні та розгортці відповідно однією та двома лініями. З’єднавши точки 1, 2 та 3, дістаємо половину трикутної грані (рис. 1.51) пропонованої поверхні.

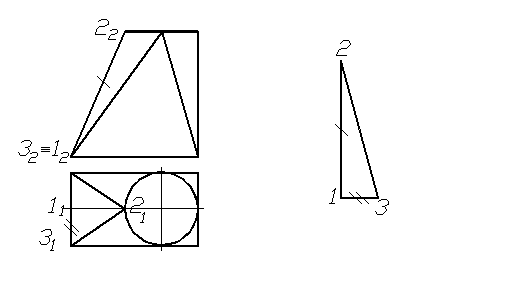
Рисунок 1.51 – Побудова елемента розгортки

Далі за трикутною гранню йде частина нахиленого конуса з вершиною у точці 3, першою твірною якого є сторона 23 трикутної грані.

Щоб побудувати розгортку конічної поверхні, необхідно розбити частину кола між точками 2 та А (основа конуса) на кілька частин (на рисунку 1.52 на три частини). Натуральна величина твірних 3С та 3В визначається способом обертання навколо проеціювальної осі, яка проходить через точку 3. Натуральна величина твірної 3А – це її фронтальна проекція. Розгортку конічної поверхні будують способом тріангуляції (рис. 1.52).

Рисунок 1.52 – Побудова розгортки конічної поверхні

Далі до розгортки необхідно додати трикутну грань 3А4, яка проектується у натуральну величину на фронтальну площину проекцій (рис. 1.53).

Рисунок 1.53 – Побудова розгортки гранної поверхні

Потім до розгортки додається конічна поверхня з вершиною у точці 4 (рис. 1.54).

Рисунок 1. 54 – Побудова розгортки конічної поверхні

Завершує побудову розгортки бічної поверхні половина трикутної грані 4F5, яка у натуральну величину проектується на профільну площину проекцій. На рисунку 1.55 наведена половина розгортки бічної поверхні пропонованої на рисунку 1.50 деталі.

Рисунок 1.56 – Розгортка складної поверхні