2.2 Визначення натуральної величини відрізка способом прямокутного трикутника
Аналізуючи
положення відрізків прямої відносно
площин проекцій, можна зробити висновок,
що лише у тому випадку, коли відрізок
прямої займає особливе положення, на
комплексному кресленні маємо натуральну
величину відрізка. Для прямих загального
положення на площини проекцій відрізок
прямої проектується із спотворенням.
При розв’язанні багатьох задач нарисної
геометрії досить часто виникає
необхідність мати натуральні величини
відрізків прямих ліній. Натуральну
величину відрізка, який займає загальне
положення, можна визначити способом
прямокутного трикутника (рис. 1.11).
Суть способу полягає в тому, що
натуральну величину відрізка (НВ)
визначають як гіпотенузу прямокутного
трикутника, у якого один катет – це
проекція відрізка на площину проекцій,
а другий – різниця відстаней кінців
відрізка від цієї площини проекцій.
Цей
спосіб проілюстрований на рисунку 1.11,
де:
АВ – відрізок у просторі; А1В1
– горизонтальна проекція відрізка;
Z
– різниця відстаней кінців відрізка
АВ від горизонтальної площини проекцій;
– кут нахилу відрізка АВ до горизонтальної
площини проекцій.
Рисунок 1.11 – Визначення натуральної величини відрізка
На рисунку 1.12 (а та б) наведений приклад визначення натуральної величини відрізків та кутів нахилу їх до відповідних площин проекцій.
а) б)
Рисунок 1.12 – Визначення натуральної величини відрізка та кутів нахилу його до площин проекцій
3. Проекції площини
Існують шість способів завдання площини у просторі: трьома точками, які не належать одній прямій, прямою та точкою, яка не належить цій прямій, двома паралельними прямими, двома прямими, які перетинаються, геометричною фігурою (відтинання площини), слідами площини.
3.1 Способи завдання площини на комплексному кресленні
На комплексному кресленні площина може бути задана:
проекціями трьох точок, які не належать одній прямій (рис. 1.13);
проекціями прямої та точки, яка не належить цій прямій (рис. 1.14);
Рисунок 1.13 Рисунок 1.14
проекціями двох паралельних прямих (рис. 1.15);
проекціями двох прямих, які перетинаються (рис. 1.16);
Рисунок 1.15 Рисунок 1.16
проекціями відтинання площини (рис. 1.17);
слідами площини (рис. 1.18).
Рисунок 1.17 Рисунок 1.18
3.2 Положення площини відносно площини проекцій
Залежно від положення заданих площин відносно площин проекцій їх поділяють на площини загального положення та площини особливого положення.
Площинами загального положення називають площини, які не перпендикулярні до жодної з площин проекцій. Приклади площин загального положення наведені на рисунках 1.13 – 1.18.
Площини особливого положення поділяють на площини проеціювальні та площини рівня.
Якщо задана площина перпендикулярна до однієї з площин проекцій, то вона на неї проектується у вигляді відрізка. Такі площини називаються проеціювальними. Залежно від того, якій площині проекцій задані площини перпендикулярні, їх називають горизонтально – проеціювальними (рис. 1.19а), фронтально – проеціювальними (рис. 1.19б) та профільно-проеціювальними (рис. 1.19в).
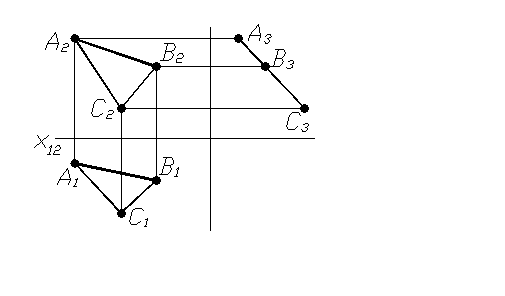
а) б) в)
Рисунок 1.19 – Площини проеціювальні
Площини рівня – це площини, які перпендикулярні одночасно до двох площин проекцій, тобто паралельні третій площині проекцій, на яку вони проектуються у натуральну величину.
Залежно від того, якій площині проекцій задана площина паралельна, площини називають площинами горизонтального рівня (рис. 1.20а), фронтального рівня (рис. 1.20б) та профільного рівня (рис. 1.20в).
а) б) в)
Рисунок 1.20 – Площини рівня